目錄

   思路【floyd+dp】：

 【程式碼實現：floyd+dp】

   思路2:並查集+二分

 【程式碼實現：並查集+二分】 

             最後來個小小的總結：

【題目描述】

一個點每過一個單位時間就會向 4 個方向擴散一個距離，如圖所示：兩個點 a 、b 連通，記作 e(a,b) 當且僅當 a 、b 的擴散區域有公共部分。連通塊的定義是塊內的任意兩個點 u、v 都必定存在路徑 e(u,a0​),e(a0​,a1​),…e(ak​,v)。                                                   給定平面上的 n 個點，問最早什麼時候它們形成一個連通塊。

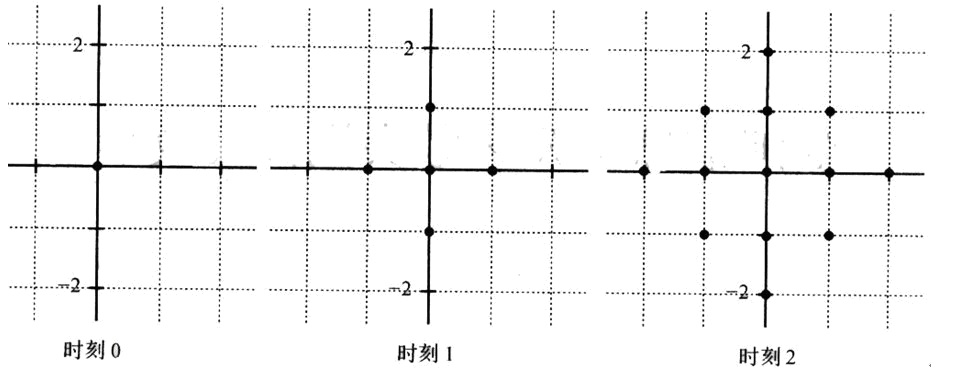
【輸入格式】

第一行一個數 n ，以下 n 行，每行一個點座標。

【輸出格式】

輸出僅一個數，表示最早的時刻所有點形成連通塊。

【樣例輸入】

2
0 0
5 5

【樣例輸出】

5

【資料範圍與提示】

對於 20% 的資料，滿足 1≤n≤5,1≤Xi​,Yi​≤50；

對於 100% 的資料，滿足 1≤n≤50,1≤Xi​,Yi​≤10^9。

思路【floyd+dp】：

首先我們一看到這道題目，最早的時刻，好的一定是首選二分對吧，但是你再細細看一下，這是一個連通圖，一個距離的連通，那就意味著什麼？意味著我們可以用最短路來求出最短距離之後在進行判斷。

跟隨我上面講了，這道題的細節也很重要

設兩個點A、B以及座標分別為

         ，則A和B兩點之間的距離為：

以上的式子在程式碼中不好表示，那就根據數學稍微改變一下：

這樣一來我們可以十分方便的把這個式子帶入到程式碼當中（絕對值的表示為，記得在前面加標頭檔案

#include<cmath>

這便是我所說的距離， 以後遇到這樣的座標距離題都可以直接用上面的公式。好我們繼續，我們求出了點兩兩之間的距離之後，就是最最最重要的一步，跑floyd，為什麼重要呢？因為沒有了這一步，你的程式碼就失敗了，floyd是幫助我們確定兩個點之間的最短距離的方向，按照最短距離的方向來延伸。

 

for(int k=1;k<=n;k++)
    for(int i=1;i<=n;i++) if(i!=k)
        for(int j=1;j<=n;j++) if(j!=i && j!=k)
            floyd[i][j]=min(floyd[i][j],floyd[i][k]+floyd[j][k]);

只有四行，三個迴圈一個計算。記住這個優秀的演算法——floyd演算法

【程式碼實現：floyd+dp】

/*
解釋一下定義：他是要存在了公共區域才算OK啊
是全部都有公共區域 
而且要求最小的時刻，那就意味著我們要讓所有點之間的距離儘可能的小
在這個方面的基礎上，最有效的辦法就是就是求任意兩點直接最短路的演算法
dijkstra演算法 / spfa演算法 / floyd演算法 都是有效的最短路演算法 
*/
#include<cmath>
#include<cstdio>
#include<cstdio>
#include<algorithm>
using namespace std;
int x[55],y[55];
int w[55][55];//記錄的是兩個點之間的距離 
int main()
{
	int n;scanf("%d",&n);
	for(int i=1;i<=n;i++)scanf("%d%d",&x[i],&y[i]);
	for(int i=1;i<=n;i++)
		for(int j=1;j<i;j++)
			w[i][j]=w[j][i]=abs(x[i]-x[j])+abs(y[i]-y[j]);//求出兩點的距離 
			//距離公式是abs(x0 - x1) + abs(y0 +y1)，
	//經過多次畫圖之後知道，其實每一次的擴充套件就是在外面多一圈 
	for(int k=1;k<=n;k++)
		for(int i=1;i<=n;i++)
			for(int j=1;j<=n;j++)
				w[i][j]=min(w[i][j],max(w[i][k],w[k][j]));
	/*
	尋找最短距離 
	仔細一看有點像floyd演算法，求任意兩點最短路的演算法
	floyd的精髓所在就是我們用三個迴圈，然後就可以判斷出
	他到底是直接到距離最短，還是經過其他點相加的路程距離最短 
	所以這一步是不可以沒有的，我們最先找到的距離公式只是片面的
	floyd才是最根本的一個距離的記錄，我也發現把這一部分刪掉就會wa掉 
	*/ 
	int ans=0;//記錄最小的時刻 
	for(int i=1;i<=n;i++)
		for(int j=1;j<=i;j++)
			ans=max(ans,w[i][j]);//ans就是更大的距離 
	printf("%d\n",(ans+1)/2); 
	/*
		兩個點連通僅當距離<=時間*2 這是推理的一條公式
		然後根據這條公式我們可以知道，w[i][j]記錄的就是距離
		而ans是最大距離的記錄成立的跑過floyd之後最短的最大距離
		（之所以要找到最大是因為我們要讓所有都連通，那就要兼顧最壞的情況） 
		所以的話，我們的ans要小於等於時間乘以2
		那麼知道距離，時間就是除以2
		然後這個+1是為了防止出錯，怎麼個出錯法呢？
		就是那些交叉的，其實差一點點才能夠聯通
		但是按照我們的演算法電腦預設連通其實只是銜接上沒有算得上是連通
		這是時候就要加多一步來實現
		（最主要的是雙數的時候沒有影響，只是影響單數的銜接情況） 
	*/ 
	return 0;
}
//https://blog.csdn.net/xianpingping/article/details/79947091
//優秀的floyd演算法的解釋部落格 

思路2:並查集+二分

首先我們為什麼要用並查集，因為要確定一個兩個點延伸之後的公共點，我們把這個公共點通過並查集找到，定義為他們的父親節點。接著就是二分來縮短距離。其實二分也很簡單，就是說實在的吧，我想到了二分，但是我沒有想到並查集，所以才會放棄二分轉戰floyd。經過這一經歷，我覺得我對並查集產生了一種好感，（原來並查集可以找距離，這個很震撼）

【程式碼實現：並查集+二分】 

#include<cstdio>
#include<cstring>
#include<algorithm> 
using namespace std;
struct node
{
	int x,y;
}a[55];
int n,d[55][55],fa[55];//d[i][j]記錄距離，fa記錄父親 
inline int abs(int x){return x>0?x:-x;}
int juli(node n1,node n2){return abs(n1.x-n2.x)+abs(n1.y-n2.y);}
int find(int x)
{
	if(x==fa[x])return x;
	else return fa[x]=find(fa[x]);
}
bool check(int x)
{
	for(int i=1;i<=n;i++)fa[i]=i;//先規定好每個點的父親節點 
	for(int i=1;i<=n;i++)
		for(int j=i+1;j<=n;j++)
			if(d[i][j]<=x*2)//同樣的距離小於兩倍的時間 
			{
				int fx=find(i),fy=find(j);
				//先找到自己共同的祖先，就是要相交的時候到達的點 
				if(fx!=fy)fa[fx]=fy;
				//如果不一樣的話，將其中一個與另一個變為一樣的 
			}
	int sum=0;
	for(int i=1;i<=n;i++)
	{
		if(fa[i]==i)sum++;//祖先相同的話，這樣的走向就成立 
		if(sum==2)return false;
		/*如果有兩個祖先的話，說明最短距離沒有找對，
		因為只能允許一個最近的祖先*/ 
	}
	return true;
}
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)scanf("%d%d",&a[i].x,&a[i].y);
	for(int i=1;i<=n;i++)
		for(int j=1;j<i;j++)
			d[i][j]=d[j][i]=juli(a[i],a[j]);
	int l=0,r=999999999,ans=0;
	while(l<=r)
	{
		int mid=(l+r)/2;
		if(check(mid)==true){r=mid-1;ans=mid;}
		//目的求最小，正確往左移 
		else l=mid+1;
	}
	printf("%d\n",ans);
	return 0;
}

最後來個小小的總結：

可以求距離的演算法（或者說和距離有關係的）

spfa演算法（bfs）

dijkstra演算法（單源最短路徑演算法）

floyd演算法（任意點之間的最短路）

並查集（找到一個共同目標為父親節點）

目前我找到的最有效最好用的就是這四個了