【貪心+並查集/優先佇列】POJ1456 Supermarket
阿新 • • 發佈:2018-12-22
Supermarket
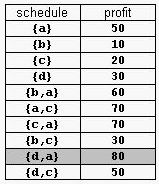
For example, consider the products Prod={a,b,c,d} with (pa,da)=(50,2), (pb,db)=(10,1), (pc,dc)=(20,2), and (pd,dd)=(30,1). The possible selling schedules are listed in table 1. For instance, the schedule Sell={d,a} shows that the selling of product d starts at time 0 and ends at time 1, while the selling of product a starts at time 1 and ends at time 2. Each of these products is sold by its deadline. Sell is the optimal schedule and its profit is 80.
Write a program that reads sets of products from an input text file and computes the profit of an optimal selling schedule for each set of products.
一開始的想法是用貪心,把每個商品利潤從高到低排序,保證利潤高的能“先”賣出去(優先順序高)。每個商品在截止時間那天賣出,如果有重複的就把時間往前推,直到找到第一個空出的時間賣掉。 寫了個簡單貪心,沒有優化,POJ上耗時141MS,程式碼如下:
| Time Limit: 2000MS | Memory Limit: 65536K | |
| Total Submissions: 17974 | Accepted: 8071 |
Description
A supermarket has a set Prod of products on sale. It earns a profit px for each product x∈Prod sold by a deadline dx that is measured as an integral number of time units starting from the moment the sale begins. Each product takes precisely one unit of time for being sold. A selling schedule is an ordered subset of products Sell ≤ Prod such that the selling of each product x∈Sell, according to the ordering of Sell, completes before the deadline dx or just when dx expires. The profit of the selling schedule is Profit(Sell)=Σ x∈SellFor example, consider the products Prod={a,b,c,d} with (pa,da)=(50,2), (pb,db)=(10,1), (pc,dc)=(20,2), and (pd,dd)=(30,1). The possible selling schedules are listed in table 1. For instance, the schedule Sell={d,a} shows that the selling of product d starts at time 0 and ends at time 1, while the selling of product a starts at time 1 and ends at time 2. Each of these products is sold by its deadline. Sell is the optimal schedule and its profit is 80.

Write a program that reads sets of products from an input text file and computes the profit of an optimal selling schedule for each set of products.
Input
A set of products starts with an integer 0 <= n <= 10000, which is the number of products in the set, and continues with n pairs pi di of integers, 1 <= pi <= 10000 and 1 <= di <= 10000, that designate the profit and the selling deadline of the i-th product. White spaces can occur freely in input. Input data terminate with an end of file and are guaranteed correct.Output
Sample Input
4 50 2 10 1 20 2 30 1 7 20 1 2 1 10 3 100 2 8 2 5 20 50 10
Sample Output
80 185
Hint
The sample input contains two product sets. The first set encodes the products from table 1. The second set is for 7 products. The profit of an optimal schedule for these products is 185. 題目連結: http://poj.org/problem?id=1456 參考題解: 思路二 思路三 題目大意是超市賣n個商品,每個商品都有自己的截止時間dx和利潤px,在截止時間之前都可以賣掉它,且每個單位時間只能賣一件。問最大獲利。 【思路一:貪心】一開始的想法是用貪心,把每個商品利潤從高到低排序,保證利潤高的能“先”賣出去(優先順序高)。每個商品在截止時間那天賣出,如果有重複的就把時間往前推,直到找到第一個空出的時間賣掉。 寫了個簡單貪心,沒有優化,POJ上耗時141MS,程式碼如下:
1 #include <iostream> 2 #include <cstring> 3 #include <cstdio> 4 #include <queue> 5 #include <algorithm> 6 using namespace std; 7 8 struct product{ 9 int px; //利潤和截止時間 10 int dx; 11 }x[10005]; 12 13 bool cmp(product a,product b){ //根據利潤從大到小排序 14 return a.px > b.px; 15 } 16 17 int main(){ 18 int n; 19 int table[10005]; 20 while(cin>>n){ 21 int sum = 0; 22 memset(x,0,sizeof(product)*10005); 23 memset(table,0,sizeof(table)); 24 for(int i = 0;i<n;i++) 25 scanf("%d%d",&x[i].px, &x[i].dx); 26 sort(x,x+n,cmp); //根據利潤排序 27 for(int i = 0;i<n;i++){ 28 int tmp = x[i].dx; 29 if(!table[tmp]){ 30 table[tmp] = 1; //如果該時間單位為空,則佔位 31 sum += x[i].px; 32 } 33 else{ 34 while(table[tmp]&&tmp>=1) tmp--; //如果該時間單位已滿,則往找前第一個空的時間單位佔位 35 if(tmp!=0){ 36 table[tmp] = 1; 37 sum += x[i].px; 38 } 39 } 40 } 41 printf("%d\n", sum); 42 } 43 return 0; 44 }
【思路二:貪心+優先佇列】 程式碼提交之後總覺得還會有別的更好的的方法,搜了搜大佬們的部落格,發現了另一種貪心思路。“ 每賣一個產品要佔用一個時間單位,所以,我們可以一個單位一個單位時間地依次決定,每個時間要賣哪個產品,並且保證每個單位時間賣出的產品都是利潤最大的,這樣便能保證最終結果是最大的。如果列舉時間從小到大的話,那麼比較麻煩,更好 的辦法是從最後一個截至時間開始往前列舉, 這樣的話,只要把截止時間大於等於這個時間段的產品都放入優先佇列,其中利潤最大的便是這時間所要的。 “ 這個思路是用貪心+優先佇列實現的,我也敲了一遍,POJ耗時63MS,程式碼如下:
1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <queue> 5 #include <algorithm> 6 using namespace std; 7 8 struct product{ 9 int px; //利潤和截止時間 10 int dx; 11 }x[10005]; 12 13 bool cmp(product a,product b){ //根據截止時間從大到小排序 14 return a.dx > b.dx; 15 } 16 17 priority_queue<int,vector<int>,less<int> > q; //從大到小排列 18 19 int main(){ 20 int n; 21 while(~scanf("%d",&n)){ 22 int sum = 0; 23 for(int i = 0;i<n;i++){ 24 scanf("%d%d",&x[i].px, &x[i].dx); 25 } 26 sort(x,x+n,cmp); 27 int pos = 0; //下標 28 while(!q.empty()) q.pop(); //清空q 29 for(int i = x[0].dx;i>=1;--i){ 30 while(pos<n && x[pos].dx == i){ //如果有相同截止時間的 31 q.push(x[pos++].px); //把截止時間相同的利潤都放進優先佇列 32 } 33 if(!q.empty()){ 34 sum+=q.top(); //把佇列中利潤最大的(即第一個)加進總和裡,然後從佇列中刪去,佇列中剩下的一定是截止時間大於等於下一個商品的 35 q.pop(); 36 } 37 } 38 printf("%d\n", sum); 39 } 40 41 return 0; 42 }
【思路三:貪心+並查集優化】
看到的第三種思路實際上是第一種思路的優化,用到了並查集。一個商品可以在它的截止時間之前賣出,且一個時間只能賣一個商品。所以從後往前,找到商品的截止時間之前的第一個空位,並在當天賣出,然後標記那天已被佔用。當時間被佔用時,把當天時間標記為它的前一個時間,表示下次搜尋空位時直接從前一個位置搜尋。用並查集優化,在往前搜尋空位的過程中,途中經過的所有位置都直接標記到最後搜到的那個空位上去,這樣再次搜尋這些點前面的空位時,可直接從上一次搜到的空位開始往前搜。這次的程式碼POJ耗時47MS,程式碼如下:
1 #include <cstdio> 2 #include <cstring> 3 #include <iostream> 4 #include <algorithm> 5 using namespace std; 6 7 const int N = 10005; 8 struct product{ 9 int px,dx; 10 }x[N]; 11 bool cmp(product a,product b){ 12 return a.px > b.px; //根據利潤從大到小排序 13 } 14 15 int f[N]; 16 int find(int x){ //找截止時間前空著的時間,返回從後往前找到的第一個 17 if(f[x] == -1) return x; //如果當前時間未被佔用,直接返回 18 return f[x] = find(f[x]); //當前時間已被佔用,從它標記處從後往前開始搜,並把搜到的第一個空位直接標記給它和中間經過的點 19 } 20 21 int main() 22 { 23 int n; 24 while(cin>>n){ 25 memset(f,-1,sizeof (f)); //全部初始化為-1,表示空位(此處不可初始化為0,否則在find步驟會產生影響) 26 for(int i = 0;i < n; i++) 27 scanf("%d%d",&x[i].px,&x[i].dx); 28 sort(x,x+n,cmp); 29 int sum = 0; 30 for(int i = 0; i < n;i++){ 31 int t = find(x[i].dx); //找到當前物品截止時間前空著的時間 32 if(t>0){ //找到的空著的時間單位不為0 33 sum += x[i].px; 34 f[t] = t-1; //表示當前時間已被佔用,下次搜尋直接搜前一個時間是否為空 35 } 36 } 37 printf("%d\n",sum); 38 } 39 40 return 0; 41 }
總結:並查集確實是個好東西,在學會的同時也不能死套模板,能把它用到實處才是真正的理解。希望下次可以自己寫出更好的優化!
