特徵離散化系列一方法綜述

數值離散化在資料探勘和發現知識(data mining and knowledge discovery)方面扮演者重要的角色。許多研究表明歸納任務(induction tasks)能從離散化(discretization)中獲益：有離散值的規則通常是更簡短，更容易理解，並且離散化能改善預測精度(predictive accuracy)。文獻中提到的很多歸納算(induction algorithms)法都需要離散特徵。所有的這些特點促進研究人員和實踐人員(researchers and practitioners)在開展機器學習或者資料探勘任務之前都要進行連續特徵離散化。在文獻中能查到很多離散化的方法。本文旨在對離散化方法做一個系統性的研究，追溯它們發展的歷史，以及這些方法對分類的影響，速度和精度之間的權衡(trade-off)。本文也給出了不同方法間的對比實驗，並對結果進行了分析。本文的貢獻主要有：對現存的離散化方法進行概述總結，對現有離散化方法進行歸類的層次化結構描述(hierarchical framework)，為進一步發展鋪路(pave the way)，對典型的離散化方法(representative discretization methods)的簡要討論，大量的試驗和分析，在不同的應用環境下選擇離散化方法的原則。同時也發現了一些需要去解決的問題，以及對離散化的進一步研究。

關鍵詞：discretization; continuous feature; data mining; classification

本文內容結構安排如下：

• 1 概述Introduction
• 2 當前狀態current status
• 3 離散化過程discretization process
• 4 離散化框架discretization framework
• 5 實驗和分析experiments and analysis
• 6 結論和下一步工作conclusion and future work

1.概述Introduction

資料通常以混合的形式出現：nominal，discrete，continuous。離散或者連續型資料屬於定序資料型別(ordinal data types)，資料之間有次序，然而對於定類資料型別(nominal data types)，資料之間並不擁有次序。對於連續型屬性其取值個數是無限大的，離散屬性取值通常是有限的。這兩種資料型別在學習分類樹/規則時是不一樣的。相比於連續屬性值，離散屬性值有一下優點：①通過離散化資料將被簡化並且減少；② 離散特徵更容易被理解，使用和解釋；③ 離散化使學習更加準確，快速；④使用離散特徵獲得的結果(decision trees,induction rules)更加緊湊，簡短，準確，結果更容易進行檢查，比較，使用和重複使用；⑤ 很多分類學習演算法只能處理離散資料。離散化是量化(quantizing)連續屬性的過程。離散化的成功可以很大程度上擴充套件(extend the borders)許多學習演算法的使用領域。

本文回顧了現存的離散化方法，標準化了離散化過程，以一個簡要的框架總結了它們，並且為進一步研究和發展提供了一些方便的參考。本文餘下的工作按照如下結構組織。Section 2總結了離散化方法的當前狀態；Section 3以統一的詞彙(unified vocabulary)討論了不同的離散化方法，定義了離散化的通用處理過程，考慮了不同的離散化結果評價方法，Section 4提出了新的用於離散化方法的層次框架(hierarchical framework)，簡潔的描述了典型的方法。當描述每一個典型的方法時，我們基於基準資料集(benchmark data set)Iris給出了離散化結果。該資料集是一個小型資料集，通常用於離散化和分類工作，在這裡使用是為了說明不同的演算法的工作過程。Section 5比較了不同方法的實驗結果，並對結果進行了分析。Section 6給出了選擇離散化方法的直到準則和下一步工作。

2.當前狀態current status

早期，諸如等寬(equal-width)，等頻(equal-frequency)等技術用於離散化。伴隨著精確度的需求以及有效的分類演算法的發展，離散化的技術得到了快速發展。過去幾年間，提出了許多離散化技術。試驗表明離散化在減小資料大小、甚至改善預測精度方面都有著很大的潛力。離散化方法朝著不同的主線發展來滿足不同的需求：監督與無監督(supervised vs, unsupervised)；動態與靜態(dynamic vs. static)；全域性與區域性(global vs. local)；自頂向下與自底向上(splitting(top-down) vs. merging(bottom-up))；直接與增量(direct vs. incremental)。

監督與無監督(supervised vs, unsupervised)：離散化是監督或者無監督，取決於離散化過程中離散化方法是否使用了分類資訊。監督離散化使用了分類資訊去指導離散化過程；然而無監督離散化卻沒有。沒有分類資訊的離散化方法類似於早期的等寬(equal-width)，等頻(equal-frequency)技術：根據使用者預先指定的寬度(range of values)或者頻率(number of instances in each interval)將連續的範圍(continuous ranges)劃分成各個子範圍(subranges)。

對於連續屬性值的分佈不是均勻分佈時，這可能不會給出好的結果。因此它對於異常值(outliers)是弱小的(vulnerale)，因為他們明顯影響了取值範圍。為了克服這個缺點，引入了監督離散化方法，分類資訊用於找到合適的用分割點(cut-points)定義的間隔(intervals)。已經設計(devised)了不同的使用分類資訊的方法去在連續屬性上尋找有意義的間隔。如果沒有分類資訊可以利用，無監督離散化方法是唯一選擇。沒有太多的無監督離散化方法在文獻中提到，可能歸因於(attribute to)離散化通常與分類任務有關。

動態與靜態(dynamic vs. static)：離散化方法的應用可能是動態的，也有可能是靜態的。所謂動態方法就是指離散化連續值是在分類器正在被建立的時候，諸如C4.5，靜態離散化先於分類任務完成。[文獻][9]對動態和靜態方法做了比較。作者也報道了當測試C4.5時使用和不使用離散化特徵時的混合性能。

全域性與區域性(global vs. local)：另一個分法(dichotomy)是全域性與區域性。區域性離散化方法是在例項空間(instance space/subset of instances)的區域性區域(localized region)進行的離散化。然而全域性離散化使用了全體例項空間進行離散化。當例項空間的一個區域被用來離散化時區域性方法通常與動態離散化方法有關。

自頂向下與自底向上(splitting(top-down) vs. merging(bottom-up))：離散化方法也可以根據自頂向下與自底向上進行劃分。自頂向下方法以一個空的分割點(cut-points/split-points)列表開始，在離散化程序中一直不斷的往這個列表中通過splitting intervals新增新的分割點。自底向上以完整的列表開始，該列表用所有的連續特徵值作為分割點，在離散化程序中一直不斷的給這個列表中通過merging intervals移除的分割點。

直接與增量(direct vs. incremental)：直接方法同時劃分K個間隔的範圍(例如equal-width，equal-frequency，K-means)，需要一個額外的輸入來決定間隔的個數。增量方法以一個簡單的離散化開始，並伴隨著改善或者提純(refinement)過程，需要停止準則來終止下一步的離散化。

綜上所述，有許多離散化方法，並以不同的維度對它們進行分組。有時對使用者而言對於手頭的資料很難找到一個合適的方法。[文獻][9,4]給出了幾種減輕這種困難的方法。我們繼續對這些關鍵問題進行全面的研究，包括：離散化過程的定義(definition of a discretization process)，效能度量(performance measure)，廣泛的對比(extensive comparison)。

本文的貢獻主要有：
1) 典型的離散化過程的簡要描述；
2) 新的層次化框架去分類文獻中提到的現存的離散化方法；
3) 對不同的離散化方法使用基準資料集對其結果進行系統論述；
4) 對從這個框架下沿著基於公開資料集的分類學習演算法的時間消耗和錯誤率這兩個維度選出的9個代表性的離散化方法進行對比；
5) 對對比結果進行詳細檢查；
6) 對不同的使用環境選用何種方法給出指導準則，給出下一步研究的方向；

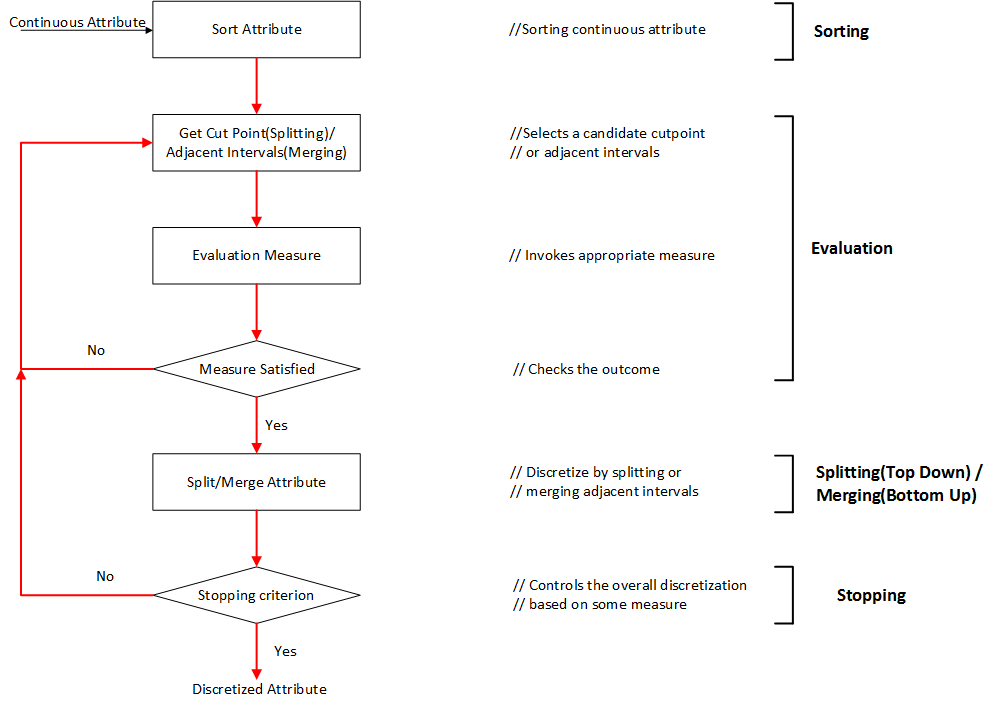
3.離散化過程discretization process

首先我們闡明(clarify)幾個術語(terms)，以對典型的離散化過程進行簡要描述。

3.1術語和符號terms and notations

特徵feature
特徵(feature)，屬性(attribute)，變數(variable)是資料的一方面。通常在收集資料之前，特徵應該被指定或選擇。特徵可能是離散的、連續的、定類的。本文我們的興趣主要在離散連續特徵的過程。接下來用M表示資料集中特徵的個數。

例項instance
例項(instance)、元組(tuple)、記錄(recor)、資料點(data point)是一次資料記錄所有特徵的特徵值。例項的集合產生資料集。通常資料集每行代表一個例項，每列代表一個特徵。用N表示資料中例項的個數。

分割點cut-point
術語分割點(cut-point)指的是連續值範圍中的一個實數值，它將這個範圍分割成兩個間隔。一個間隔是小於等於這個分割點的，另一個是大於分割點的。例如，一個連續的間隔[a,b]被分割成[a,c]和[c,b]，值c就是分割點。分割點(cut-point)也被叫做分離點(split-point)。

元數arity
術語元數(arity)在離散化環境中就是間隔或者劃分的個數。在離散化連續特徵之前，元數被設定成k-連續特徵的劃分數。最大的分割點數是k-1。離散化過程減小了元數，但是在元數和分類或其他任務的效能之間做了折中。元數太大，會使學習過程變得更長，但是元數太小，會影響預測的精度。

3.2典型離散化過程a typical discretization process

使用“典型”，指的是單變數離散化。離散化可能是單變數的，也可能是多變數的。單變數離散化(univariate discretization)一次只離散化一個連續特徵，然而多變數離散化(multivariate discretization)同時考慮多個特徵。本文主要考慮了單變數離散化，文章末尾簡單討論了多變數離散化，作為單變數離散化的擴充套件。
典型的離散化過程通常由以下4步組成：
1) sort對離散化的特徵的連續值進行排序；
2) evaluate對為了合併的劃分的或者鄰近的間隔，評估分割點；
3) split or merge通過一些準則，劃分或者合併連續值的間隔；
4) stop停止離散化。

排序sorting
對特徵的連續值進行降序或者升序排序都可以。如果不關心在離散化時進行排序，那麼排序的計算代價將是非常昂貴的。對於所有的特徵，排序在離散化開始之前完成，這將是一個全域性處理(global treatment)，適用於將整個例項空間離散化。如果排序在過程的每一次迭代時完成，這將是一個區域性處理(local treatment)，僅對整個例項空間的一個區域進行離散化。

選擇分割點 choosing a cut-point
排序之後，離散化過程接下來的一步是尋找最好的分割點，對連續值的範圍進行劃分，或者尋找最好的一對鄰近的間隔進行合併。一個典型的評價函式用來決定一次劃分或者合併與類別標籤的關係。文獻中提到很多評價函式，諸如：熵測量、統計測量。關於評價函式與它們的應用將在下一小節進行討論。

劃分/合併Splitting/merging
正如我們所知，對已自頂向下的方法，間隔是劃分；然而對於自底向上的方法，間隔是合併。對於劃分，需要評價分割點，選擇最好的一個，並將連續值範圍劃分成兩部分。分別對每一部分進行離散化直到滿足停止準則。對於合併，評估鄰近的間隔，找到最好的間隔進行合併。離散過程一直持續，間隔數隨之減少，直到滿足停止準則。

停止準則stopping criteria
停止準則是為了終止離散過程。它經常被元數和精度的折中所支配，因為這兩個是正互相關的(positively correlated)。我們可以將k作為離散化的結果的元數設定一個上界，事實上，上界k的設定是遠小於N的，假設沒有特徵連續值的副本，停止準則可能是非常簡單的，諸如在一開始固定間隔數，或者一個稍微複雜一些的如評價函式。在下一章節描述不同的停止準則。

3.3離散化方法對比comparison of discretization methods

針對不同離散化方法獲得的離散化資料，哪一個更好呢？看起來是一個簡單的問題，卻很難用簡單的答案來回答。這是因為不同的方法之間的比較是一個複雜的問題，它依賴於使用者在某一個特殊應用的需求。說複雜是因為不同方法的評價可以從多個方面來進行。我們列舉了3個重要的維度：(1)總的間隔數，直觀的，間隔點越少，離散化結果越好；但是強加於資料呈現是有限的。這導致第二個維度。(2)離散化引起的不一致性的個數。它不應該大於離散化之前原始資料的不一致數。如果最終結果是從資料訓練一個分類器，應該考慮另一個觀點。(3)預測精度-離散化對預測精度的改善。簡言之，我們至少需要三個維度的考慮：簡化(simplicity)、一致性(consistency)、精度(accuracy)。理想情況下，最好的離散化結果在這三方面應都有最高的得分。但事實上，它是不可能達到的，或者不需要的。為不同的離散化方法在這三方面提供一個均衡的觀點也是本文的目標。

簡化(simplicity)使用分割點的總數來定義的。精確度(accuracy)在交叉驗證模式下執行分類器可以獲得。一致性(consistency)是最小的不一致性計數值，可以通過以下3步計算而來(下面的描述中，模式pattern指沒有類別標籤的例項)：(1)如果兩個例項有著相同的屬性值，但是類別標籤不一樣，則這兩個例項是不一致的；例如，如果兩個例項是(0 1;0)和(0 1;1)，它們就是不一致的。(2)一個模式的計數值是這個模式出現在資料中的次數減去最大的類別標籤數；例如，假設有n個例項與這個模式相匹配，其中label1的個數是c1, label2的個數是c2，label3的個數是c3，其中c1+c2+c3=n。如果c3是這三個中最大的，則該模式的不一致性計數值為(n-c3)。(3)總的不一致性計數是一個特徵集合中所有可能的模式的不一致性計數值之和。

4.離散化框架discretization framework

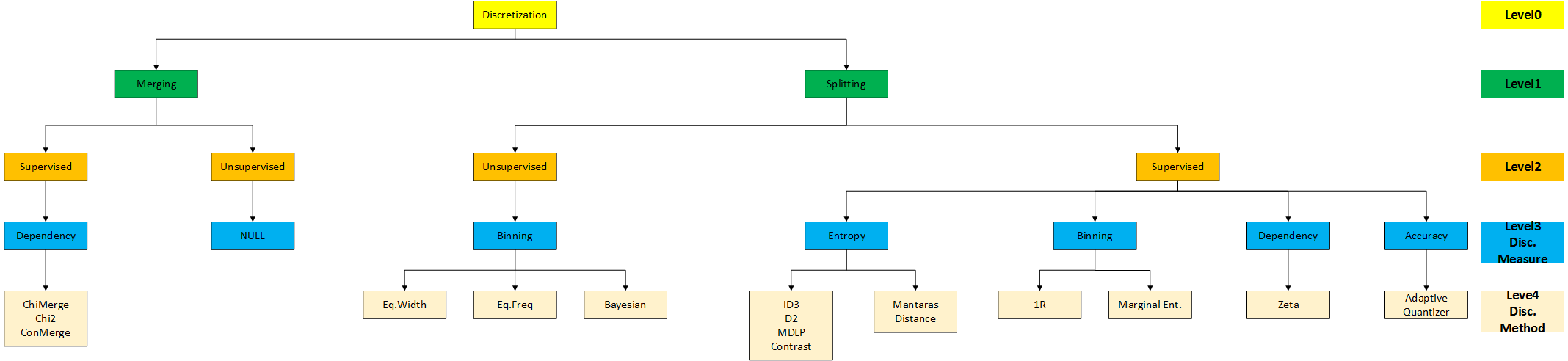
文獻中提到很多離散化方法。正如上面所述的一樣，根據不同的維度可以對這些方法進行分類。即：監督與無監督(supervised vs, unsupervised)；動態與靜態(dynamic vs. static)；全域性與區域性(global vs. local)；自頂向下與自底向上(splitting(top-down) vs. merging(bottom-up))；直接與增量(direct vs. incremental)。可以根據這些維度的不同組合來對這些方法進行分組。我們希望構建一個系統的、可擴充套件的、能覆蓋現在所有方法的框架。文獻中提到的每一種離散化方法離散化一個特徵：或者對連續值劃分間隔；或者合併鄰近的間隔。劃分和合並根據是否使用分類資訊可進一步分組成監督與無監督。
鑑於這些方面的考慮，我們提出了層次化框架(hierarchical framework)，如下圖所示。

通過兩種方法：劃分和合並，描述了不同的離散化測量(level1)。接著我們考慮了方式是監督還是無監督(level2)。進一步我們將使用相同離散化度量方法的分組在一起(level3)，例如分箱(binning)和熵(entropy)。如下圖所示，監督與無監督劃分決定了不同的度量方法。因此概念上有用的劃分將不再詳細講述。

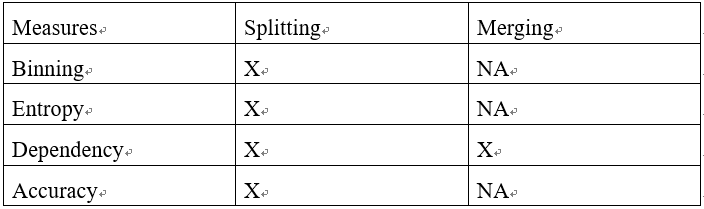
我們將討論如下表所示的基於劃分和合並的分類方法的現存的不同的度量方式。

在以下兩個小節，將選擇典型的方法進行深入討論(in-deep discussion)。它們相關的或者派生的(related or derived)度量方法也會簡要涉及。對每一個離散化度量方式，我們主要給出：
(1). 度量方式的定義；
(2). 在離散化方法中的應用；
(3). 使用的停止準則；
(4). 對Iris資料集的離散化結果：每一個屬性的分割點；
在小節的最後，出於對比目的，我們給出了所有離散化度量方式的結果列表：不一致性的個數、離散化的分割點。

4.1劃分方法splitting method

我們以用於劃分離散化方法的通用演算法開始。

在離散化過程中劃分演算法(splitting algorithm)由4步組成，它們是：
(1). 對特徵值排序；
(2). 搜尋合適的分割點；
(3). 根據分割點劃分連續值的範圍；
(4). 當滿足停止準則的時候停止離散化否則繼續；
文獻中提到很多劃分離散化度量方法：分箱(binning)、熵(entropy)、獨立性(dependency)、精確度(accuracy)。

注：這些方法我們將開設獨立的部落格去說明討論。

分箱binning

• Equal width or frequency
• 1R

熵entropy

• ID3 type
• D2
• Ent-MDLP
• Mantaras distance

獨立性dependency

• Zeta

精確度accuracy

• adaptive quantizer

4.2合併方法merging method

我們以採用合併或者自底向上方法的離散化通用演算法開始。

在離散化過程中合併演算法由4個重要步驟組成，它們是：
(1). 對值進行排序；
(2). 找到最好的兩個相鄰間隔；
(3). 把這一對合併成一個間隔；
(4). 滿足停止條件時終止。

注：這些方法我們將開設獨立的部落格去說明討論。

chi-square measure

ChiMerge

chi2

4.3討論discussion

我們已經回顧了在劃分和合並歸類情況下的典型離散化方法。大部分方法是基於劃分方法的。我們使用Iris資料集作為一個例子展示了不同的離散化方法的結果。兩種度量方式(number of inconsistencies and number of cut-points)直覺上的關係是：分割點越多，不一致計數越少。仔細觀察表明(closer look)讓兩個計數值都少可能有一個妥協(middle ground)的方法。因此，我們應該旨在去讓兩個數值(number of inconsistencies and number of cut-points)都小。我們確實發現對於Iris資料一些方法比其他方法要好：Ent-MDLP是劃分方法裡邊最好的；chi2是合併方法裡邊最好的。Chi2也表明，通過考慮一定程度的不一致性，在兩種度量方式之間達到折中也是可能的。除離散化之外(in addition to)，Chi2也移除了具有一定程度的不一致性的特徵。

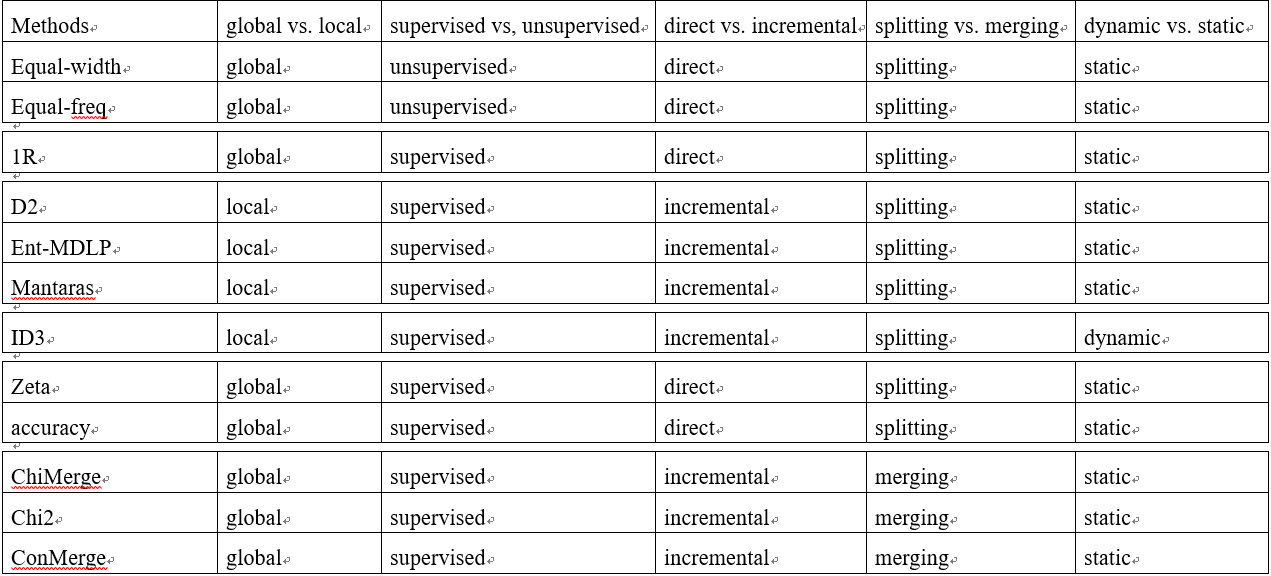
在section2，我們通過5種不同的維度回顧了監督與無監督(supervised vs, unsupervised)；動態與靜態(dynamic vs. static)；全域性與區域性(global vs. local)；自頂向下與自底向上(splitting(top-down) vs. merging(bottom-up))；直接與增量(direct vs. incremental)的離散化方法。在多維觀點(muti-dimensional view)下我們又得到了另外一種型別的分組。如下表所示：