早期的三維場景繪製，顯示卡只是為螢幕上顯示畫素提供一個快取，所有的圖形處理都是由CPU單獨完成，而渲染一個複雜的三維場景，需要在短時間內處理幾百萬個三角形頂點和光柵化上百萬個畫素，擅長於執行序列工作的CPU實際上難以勝任這項任務，速度上達不到要求。所以，若要求在PC上實時生成三維影象，則將犧牲質量，導致畫面很粗糙。現階段，GPU的發展極大地提高了計算機圖形處理的速度和圖形質量，並促使圖形處理功能不斷從CPU向GPU轉移，如頂點座標轉換計算等，而且GPU本身亦不斷增強了圖形處理的各種高階功能，如遮擋剔除、紋理對映、透明與半透明處理、景深效果等。

本章將從GPU特點與其支援下的渲染流程角度出發，提出採用GPU具備的繪製到紋理功能，獲取上幀資訊，進行可見性判斷，從而剔除不必要渲染的場景模型，實現場景加速繪製的方法；針對過大或不符尺寸的紋理導致GPU因視訊記憶體不足而頻繁交換的問題，介紹Mipmap技術與Clipmap技術；最後，引入面向GPU頂點快取的通用渲染順序與多級快取的格網布局方法，並配合上一章介紹的視點相關的實時有選擇性細化方法，期望進一步提升

5.1 引言

我們正處在資訊科技高速發展的年代，而計算機圖形處理技術的發展速度則是計算機應用行業中最快的。無論是從用於圖形設計的硬體、視覺化應用的畫面品質、各種三維遊戲和模擬場景的畫面處理、使用圖形技術的互動式應用程式還是從計算機動畫等方面來看都是如此。十多年前用於計算機圖形設計的硬體還是那種價值昂貴的圖形工作站，而如今基本上都已經發展為單晶片的圖形處理器。

1995年，PC機領域第一款帶有GPU的顯示卡3dfx Voodoo出來，使得遊戲的速度、畫質取得了一個飛躍。3dfx Voodoo有兩個主要的特徵：深度緩衝區(z-buffer)和紋理對映（texture mapping）。z-buffer執行“隱藏面消除”這一工作，可以避免渲染不可視的無效畫素。利用紋理對映功能則能十分逼真地表達物體表面細節。1999年，第二代GPU (NVIDIA GeForce256,GeForce 2和ATI Radeon 7500)包括了圖形的幾何變換與光照計算功能(Transformation and Lighting, T&L)。而在此之前T&L都是由CPU完成的，這對CPU來說是很複雜的計算。第二代GPU解決了系統的這個瓶頸，減輕了CPU的負荷，速度明顯提高了。但是由於是固定的渲染流水線，缺乏靈活性，束縛了開發人員的創造性。2001年，NIVIDA公司的GeForce 3首先引入了可程式設計的頂點著色器（Vertex Shader）單元。緊接著在2002年，可程式設計的畫素著色器(Pixel Shader)單元也加入進來。在繪製時，GPU首先接收CPU以三角形頂點形式傳送的幾何資料。然後由可程式設計的頂點著色器單元進行處理，完成幾何變換與頂點屬性計算等功能。接著，這些三維空間的三角形由光柵生成器轉換為二維螢幕上的畫素。每個畫素的最終顏色值都通過執行在畫素著色器上的小程式運算得到。目前三維遊戲和模擬場景藉助於GPU，在資料量不是很大並且光照陰影處理不是太複雜的情況下，已經能夠實時生成細膩、逼真的畫面。

           GPU的功能更新很迅速，運算速度也越來越快。2004年推出的GPU Nvidia GeForce 6800 Ultra可達到峰值40 Gigaflops( 1 Gigaflops＝1秒鐘進行10億次的浮點運算)，2005年剛釋出的 Nvidia GeForce 7800 GTX更是將峰值提高至169 Gigaflops。而Intel 3GHz Pentium 4採用SSE指令集只能達到6 Gigaflops（見圖5—1）。GPU的運算速度如此之快，主要得益於GPU是面向圖形實時渲染定製的，具有兩點主要特徵：超長流水線與平行計算。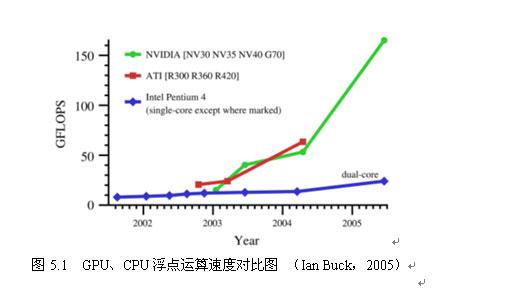


 

採用流水線方法，比簡單的序列方式能提前完成圖形渲染任務。為了提高流水線的速度，可以將任務劃分成更小的單元，這樣流水線的級數就會增加。CPU的設計中就使用了流水線原理，奔騰IV就有20級的流水線。但是流水線級數並不是越多越好，級數太多，一條指令從開始進入流水線到最後被執行完畢之間的延遲間隔會相當大。換句話說，當流水線級數過多時，控制檯發出一條指令後，要經過較長時間才會真正生效，這不適合快速反應要求很高的場合。CPU的設計目標要求有很小的延遲，所以這是CPU並不採用過多流水線級數的原因之一。另外流水線只有在滿載時，才能發揮出最佳效率來。由於CPU執行的程式碼中有很多分支語句，因此長流水線需要儘量保持其在滿負荷狀態。而一旦預測分支失敗，就會清除流水線中滯留的大量無用指令，同時將新指令流重新注入流水線。如果流水線階段過多的話，充滿整個流水線就需要很長的時間，這樣使流水線保持滿載的機會不多，速度反而下降了。所以權衡利弊，CPU不會使用深度流水線。

但是GPU卻採用了幾百級的流水線，這是因為GPU應用可以忍受大的延遲。時鐘週期與流水線級數的乘積遠小於顯示每幀畫面的時間，所以對GPU來說延遲不成問題，而且GPU中執行的象元片段程式中，分支語句用的很少（在早期的GPU中，甚至不提供動態的分支語句）。因此，GPU的流水線深度變大後，利大於弊，大大提升了整體效能。

GPU的執行速度很快，但是當執行從記憶體中獲取紋理資料這樣的指令時（由於記憶體訪問是瓶頸，此操作比較緩慢），整個流水線便出現長時間停頓。在CPU內部，使用多級Cache來提高訪問記憶體的速度。GPU中也使用Cache，倘若Cache命中率不高，則僅使用Cache就不能很好的解決這個問題。所以，為了保持流水線忙碌，GPU工作時又使用了多執行緒機制(Multi-threading)。當畫素著色器針對某個畫素的執行緒A遇到存取紋理的指令時，GPU會馬上切換到另外一個執行緒B，對另一個畫素進行處理。等到紋理從記憶體中取回時，可再切換到執行緒A。使用這種方法有一個前提，執行緒A與執行緒B沒有資料依賴性,也就是說兩執行緒之間無需通訊。如果執行緒B需要執行緒A提供某些資料，那麼即使切換到執行緒B，執行緒B仍是無法執行，流水線還是處於空閒狀態。需要說明的是，圖形渲染本質上是一個並行任務。無論是CPU送給GPU的頂點資料，還是GPU光柵生成器產生的畫素資料都是互不相關的，可以並行地獨立處理。而且頂點資料（XYZW），畫素資料（RGBA）一般都用四元數表示，適合於平行計算。此外，紋理片要麼只能讀取，要麼只能寫入，不允許可讀可寫，從而解決了存貯器訪問的讀寫衝突。GPU這種對記憶體使用的約束也進一步保證了並行處理的順利完成。

為了進一步提高並行度，可以增加流水線的條數。多條流水線可以在單一控制部件的集中控制下執行，也可以獨立執行。在單指令多資料流（SIMD）的結構中，單一控制部件向每條流水線分派指令，同樣的指令被所有處理部件同時執行。另外一種控制結構是多指令多資料流（MIMD），每條流水線都能夠獨立於其他流水線執行不同的程式。GeForce 6800 Ultra的頂點著色器流水線使用MIMD方式控制，畫素著色器流水線使用SIMD結構。MIMD能比較有效率地執行分支程式，而SIMD適合於大資料量的像元處理。

總的看來，相對於並行機而言，圖形卡提供的並行性雖然很弱，但它在十分廉價的基礎上為很多應用提供了一個很好的並行方案，尤其是對於圖形本身的應用來說。新的圖形硬體在圖形渲染上的優勢還包括：

1) 在頂點級和畫素級提供了靈活的可程式設計特性；

2) 減少了GPU與CPU的資料通訊。尤其是當整個應用針對圖形生成的時候，不再需要在CPU與GPU之間進行多次資料交換，從而可以讓CPU解放出來完成其它的任務；

3) GPU相對於CPU來說，更適應傳輸大塊的資料，雖然CPU上有Cache以加速整個計算過程，但CPU上的Cache相對於圖形卡視訊記憶體來說太小，一般只有64KB，而現在的視訊記憶體大多都在64M以上，由此可見一斑；

4) 支援繪製到紋理的功能(Render-to-Texture/pbuffer)，從而避免將計算結果拷貝到紋理這一比較費時的過程；

5) 支援依賴紋理功能，以方便資料的索引訪問，可以將紋理作為記憶體來使用。

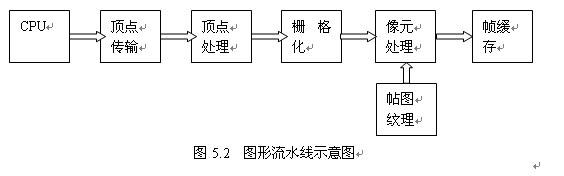
首先根據圖5.2粗略說明一下當前普遍流行的AGP（Accelerated Graphics Port，圖形加速埠）顯示卡的渲染流程。

    每次渲染過程都包括頂點處理（Vertex Processing）和畫素處理（Pixel Processing）兩個主要功能模組的執行。首先，顯示卡從AGP匯流排接收頂點資料。這些資料包括位置、法線、貼圖座標（如果是麵包可能更需要貼圖，也就是說貼圖座標不是必需的）等等，這些都是未經過任何變換，也就是在物體本地空間（Object Space）下的原始座標。每個頂點依次被送入頂點處理單元，在這裡進行座標變換、光照計算（如果是每頂點光照）等工作，變換的結果是把每個三角形變換置螢幕空間下直接可用。這裡用到的變換矩陣、燈光等資訊都是處理每一批頂點時一次性傳給顯示卡的，作為顯示卡的資源。頂點處理圈定了三角形的範圍，接下來就要逐畫素地填充這個三角形了。填充哪些畫素是靠對頂點螢幕座標的線性插值來決定的。畫素的其他一些必要引數，如顏色，貼圖座標等也是通過對上一步計算出來的頂點的這些屬性進行插值得到的。另外每個畫素還要通過深度檢測和模板檢測決定最終是否繪製。需要繪製的畫素被送進畫素處理模組，進行貼影象素取值，貼圖混合等工作，必要的話每畫素光照也在這裡完成。這裡貼圖等資訊也是作為顯示卡的資源。畫素最終的處理結果被放進幀緩衝。
       
       

5.2上幀資訊提取

可程式設計圖形顯示卡的出現增加了滿足人們對三維模擬場景更加逼真、更加流暢顯示等方面需求的機會。這些商用顯示卡已經被廣泛的應用，因此相關關鍵技術的研究變得越來越迫切。如何從上一幀影象提取顏色、深度等資訊來指導輸入到圖形流水線的場景中模型結點的選擇、更新，如何在硬體支援下優化渲染流程等是有意義的研究內容。

針對大資料量三維模擬場景，從三維模型成像機理等方面對大資料量模擬場景中目標的載入、選取和消隱進行了深入的分析之後，利用視覺成像理論、次緩衝區（pBuffer）技術和簡化方法等，對大資料量模擬場景開展加速選擇和更新等方面的研究工作。為提取上幀資訊，採用GPU的繪製到紋理功能，進行可見性判斷，剔除不必要繪製的場景模型，實現場景加速繪製的優化處理，採取的具體方法如下：

若場景範圍大或三維模型的尺度大，其在繪製選擇、繪製和渲染等流程後，顯示在螢幕上時往往有延遲現象。現考慮，將原始模型和對應的最簡化版或外框架作為兩個結點進行顯示，但分配原始模型在主緩衝區上，分配其對應的框架模型在新建的次緩衝區（pBuffer）上。由於兩個緩衝區大小是同比例的，並共享同一個相機，那麼兩種模型從投影轉換到最後的輸出顯示，即是反應同步的，在結果上也是近似的。由於顯示的大小是同比例的，但在流程中柵格化等操作會影響畫素的顯示，所以說結果是近似的。在每一幀（或者每5幀，要求人眼分辨不出來）結束後，讀取pBuffer上的畫素（一般RGB格式）到陣列中，迴圈判斷每個陣列元素的顏色，記錄下各種顏色的數量。由於在建立框架模型時分配了每個模型物件相異的顏色，從而此時通過顏色能判斷出pBuffer和主緩衝區上顯示出來的到底是哪些模型。用得到的結果指導下一個週期的原始模型中選擇哪些子集。這樣做的好處是，不用將整個大資料量的原始模型進行一遍區域性到世界座標系，再到視點座標系，最後透視變換、裁減等操作。只是將剔除視見體外和被遮擋的物體後剩餘的模型交給渲染流程，因而能節約計算、儲存等資源，加快顯示速度。

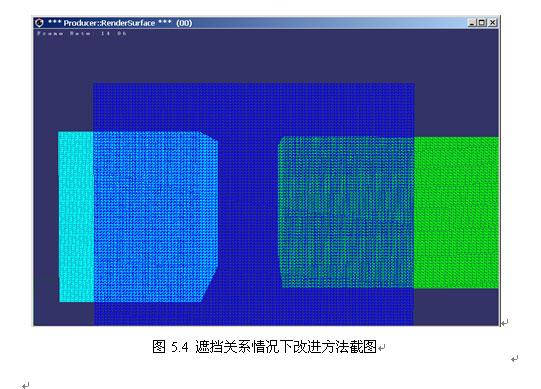
      初步實驗結果見圖5.3與圖5.4，其中由7個立方體模型組成的場景檔案大小為130M, 三角型個數70多萬個。在沒有遮擋關係的情況下，普通與改進方法下幀速均為5.4幀每秒；在有遮擋關係情況下，普通方法下幀速保持不變，還為5.4幀每秒，而改進方法下幀速增加到12.5幀每秒左右。
      
           
 

5.3 針對GPU的紋理優化處理

紋理對映(Texture Mapping)是繪製複雜場景真實感圖形最為常用的技術，它可以通過紋理來表達表面豐富的幾何細節和光照細節，甚至可以通過對映後紋理的變形來表達物體的幾何形狀：在未增加物體多邊形數情況下，增強了物體的真實感效果。

但過大或是不符尺寸的貼圖，將佔用太多的紋理頻寬，導致GPU因視訊記憶體不足而頻繁交換，採取的措施是：儘量縮小貼圖或使用Mipmap技術。Mipmap技術的核心就是紋理的LOD。高解析度的Mipmap影象用於接近觀察者的物體，當物體逐漸遠離觀察者時，使用低解析度的影象。Mipmap可以提高場景渲染的質量。

Mipmap對映技術是快速的查詢技術，快就快在它在互動前預先生成了紋理影象的一系列的基本取樣資料，形成紋理LOD模型，在互動過程中系統能快速應用紋理LOD生成逼真視景。這一優點對實時互動系統中的紋理對映至關重要，但是根據紋理對映的應用技術，對於大紋理資料是不能將整個紋理Mipmap駐留在有限的硬體紋理記憶體和系統記憶體中的，同時，由於頻寬的限制，也存在著互動前載入整個紋理需要漫長的時間。

以前解決有效物理紋理記憶體大的紋理對映問題，比如地形紋理，常常採用根據地形模型把原始紋理影象分割成大量的小片紋理，使這些小紋理能適應物理的紋理記憶體。

    現普遍採用Clipmap方法是，採用首先建立原始影象的Mipmap，而不是裝載時才建立，這對比較大的紋理來說是重要的；其次，把建立的Mipmap各層儲存在硬碟上，只把裁減下來的Mipmap部分即Clipmap調入紋理記憶體用於實時繪製。

 

5.4 針對GPU的幾何資料優化處理

從理論上分析，一旦CPU使用率達到100%，再考慮優化問題，則能夠提升的空間將是非常有限的，因為CPU的頻率決定了每幀呼叫繪製幾何元素集合的次數，所以應該儘量減少呼叫次數，增加批處理中的三角形個數。                    太多的呼叫次數，只會讓CPU忙於通訊，而GPU卻一直在空閒；另一方面來看，太少的三角形數量也滿足不了GPU的處理容量。

5.4.2.1面向GPU頂點快取的通用渲染順序

計算機圖形學應用的趨勢是大量使用多邊形來增強影象的真實性，這種趨勢隨著近來圖形硬體的發展，特別是GPU在低端顯示裝置上的出現而特別明顯。GPU意味著圖形介面卡能完成掃描轉換，也能完成3D幾何投影和陰影計算。因此，場景幾何處理不再如同過去那樣是最大的瓶頸。

為了加快處理幾何頂點元素，GPU保留了固定尺寸的先進先出（First Input First Output，FIFO）頂點快取，通過此種方式進行頂點遍歷。而渲染以三角形為基礎的通用三維格網，每個頂點參與處理的次數可能大於一次，根據對大多數格網的統計，平均每個頂點參與六個三角形的繪製。我們知道，處理快取頂點將比處理非快取頂點快得多。因此，為了最大限度的使用快取，必須以保留區域性相關性的順序渲染格網三角形。這個三角形依次渲染的順序被稱作格網渲染順序。一個好的渲染順序能最小化三角形的快取錯失數，稱作平均快取錯失率（Average Cache Missing Ratio，ACMR），因為典型格網的三角形數量接近頂點數量的兩倍，倘若在圖形渲染時頂點資料需要第一次從外部調入快取，這算作一次錯失，而其它繪製的時候，頂點資料不錯失，那麼下限數值為0.5；倘若繪製每個三角形的三個頂點時候資料都錯失，上限範圍達到3.0。所以理論上ACMR取值在0.5與3.0之間。注意，此順序不必要是連續的，在渲染順序上相連線的三角形不一定在格網空間上是相連線的。

3D格網通常以任意的三角形序列排列，其每個三角形又以指向頂點列表的三個頂點索引標明。普通渲染器就按照檔案中順序將三角形送入圖形流水線，得到一般的效能。更復雜的渲染器使用三角形條帶技術，能以FIFO頂點快取尺寸為2來渲染三角形，這實際上是3D硬體的標準部件。Akeley等（1990）描述了產生三角形條帶的演算法。然而由於快取的有限尺寸，能證明在這種快取尺寸下不能將ACMR降低到1.0以下。Hoppe（1999）提出一種演算法來產生面向透明FIFO快取的渲染順序，從實驗上展現其演算法對任意的頂點快取產生渲染順序，其ACMR不會明顯差於Chow的演算法。然而所有演算法的一個主要問題，是必須事先知道快取尺寸，對某個快取尺寸產生的渲染順序，當使用到一個更小尺寸的快取時渲染格網產生的結果也許遠離優化目標。

另外一個現有演算法的缺陷是不能推廣到累進格網。累進格網不同於固定解析度格網，格網連通性是動態的，所以不可能預先計算三角形條帶。格網是不斷變化，渲染順序也必須隨之變化。這方面工作有El-Sana（1999）提出保持累進格網的三角形條帶方法。另外，Hoppe（1997）採用在每一幀的時候，使用一種貪婪演算法來產生三角形條帶。此演算法遍歷活動三角面 ，並在任何沒有被渲染的面之處，開始一個新的三角形條帶。然後，檢查是否有鄰接面還沒有被渲染，就這樣，連線條帶。為了降低圖形狀態的變更，僅僅只有相同材質的鄰接區域被考慮。為降低流水線負擔，傾向於連續螺旋型三角形條帶。但條帶達到結束末端時候，對連結串列 遍歷重新開始。面資料結構中有一個標誌來記錄已經渲染的面，下次渲染時這些標誌會被清空。

空間填充曲線實際上是在某種程度上保留區域性相關性的多維格網單元遍歷。普遍目標是產生一種渲染順序，當每個三角形渲染時候，希望儘可能多的三角形頂點已經存在於快取中。如果不是這樣，快取錯失開始計數。

下面介紹的遞迴切割方法是受傳統空間填充曲線啟發，而最小線性安排（Minimum Linear Arrangement, 簡稱MLA）方法是通過求解優化問題得到答案（Bogomjakov, A., Gotsman, 2001）。

     遞迴切割方法。在四邊形格網（其尺寸為2的冪）上傳統的空間填充曲線有良好的區域性相關性。對於規則三角網（取代四邊形格網）容易使用Hilbert曲線來產生渲染順序。Hilbert建立過程是：將格網分為四塊（每塊相同）；遞迴的渲染第一塊中所有三角形，然後遞迴的渲染第二塊中的所有三角形，依此類推。當格網僅包含幾個三角形時遞迴終止。注意，第一塊中最後一個三角形鄰近第二塊中第一個三角形，對於第三和第四塊是一樣的處理。由於格網結構是規則的，將有可能達到目標，並保證曲線連續。Hilbert曲線的建立提示了下面類似的不規則三角網的遞迴程式：分割槽格網到兩個近似相同的子網。首先渲染第一個格網，接著是第二個。同時保證，第一個子網的結束頂點是鄰近的第二個子網的入口頂點。為了更加精確，需要找到一種平衡切分，產生兩個尺寸大致相同的頂點集合，如果邊界處的切割邊數量少就更好。程式首先渲染左邊子網，然後是跨越切割邊的三角形，接著是右邊子網。
    

 

這意味著所有參與一條超邊的頂點應該被對映到鄰近區域中。

格網渲染問題也能被看成MLA的一個例項。超圖的頂點對應著格網的三角形，超邊集合對應著格網頂點集合。一條超圖的邊聯絡著入射到相同格網頂點的所有三角形。超邊的長度意味著格網頂點上第一個和最後一個三角形的渲染順序距離。

本文研究大資料量場景的實時渲染，並在上一章介紹了應用累進格網技術來提高渲染效能。應用中，場景的多邊形數量實時改變。對於給定的更新記錄序列，必須不僅生成最高解析度的渲染順序，也有對應的更新記錄的順序。這樣，在低解析度時也能連續較好的執行。

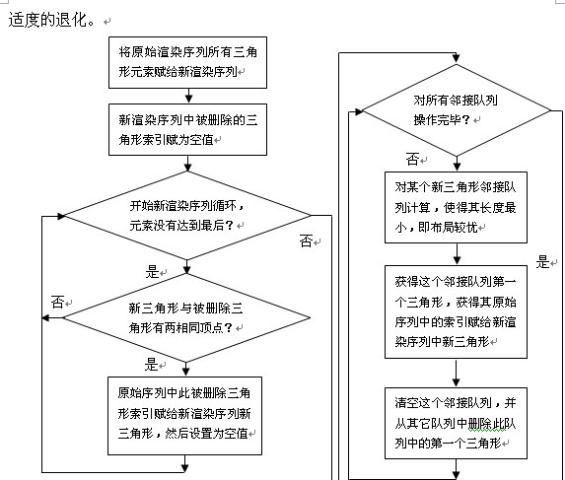
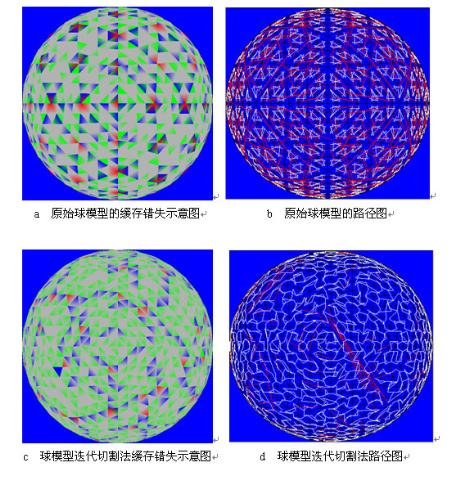
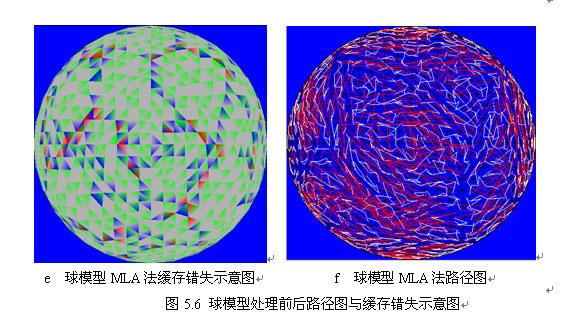
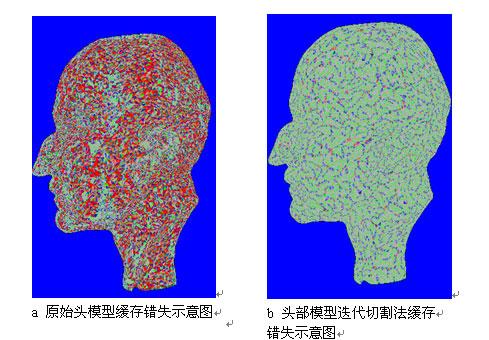
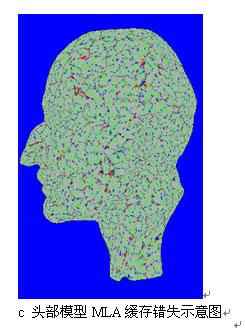
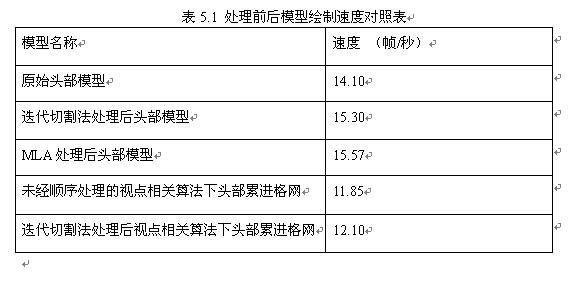
採用頂點快取個數為16的模擬程式對球與頭部三維模型進行迭代切割法與MLA演算法處理後與原始渲染順序的對於實驗。在渲染順序路徑圖中，相鄰三角形用白色線段表示，而紅色線段表示繪製三角形時產生了跳躍現象，即沒有繪製相鄰三角形。迭代切割法中基本是白色線段，說明按照相鄰三角形路徑繪製。在示意圖中，每一種顏色標誌對應頂點的不同快取錯失數量。假設頂點 參與三角形 繪製。如果 的角是灰色的，意味著 繪製時候沒有錯失 。綠色表示第一次錯失 ；藍色表示第二次錯失 ；紅色代表三次或更多次數錯失。對每個頂點來說，都會有一個綠色角，因為第一次總要將頂點載入到快取中。好的渲染順序目標就是使得灰色儘量多，而藍與紅色儘量少。從圖5.6與圖5.7中明顯看出，原始模型的紅色角多，而處理過的模型，無論採用的是迭代切割演算法或MLA演算法，綠色與藍色角多而紅色角少，這意味著經過處理的模型快取錯失數量減低。通過表5.1的統計資料得到處理後的模型渲染速度有提高的結論。

5.4.2.2面向多級快取的格網布局

處理大資料量格網的演算法利用了CPU和GPU的計算能力，用於互動顯示和幾何應用。在近十年，處理器與主儲存器之間的差距已經在擴大。結果是，系統架構不斷的使用快取和儲存層級來避免記憶體等待時間。儲存層級的不同層次的訪問時間也有很大不同。在某些情況下，一個程式的執行時間可看成是快取訪問模式的函式，並與其操作次數有很大相關性。

為了設計有效的快取演算法來處理大資料量格網，兩個通用的減低快取錯失的技術是：1）計算重排序：提高程式的區域性性，這能通過編譯器優化或人工調整達到；2）資料佈局優化：依據訪問模式計算快取連貫的資料佈局（Yoon, S.-E., Salomom, B., Gayle, R., Mannocha, D , 2004）。

快取有效演算法能被分類為快取介意的與快取非介意的。快取介意演算法使用快取引數，如分塊大小。與此相反，快取非介意演算法不用事先知道任何快取引數。快取有效演算法方面有大量研究工作，服務於一些應用，比如數值程式、排序、幾何計算、矩陣乘法、FFT和圖形演算法。面向這些應用，大多數演算法重組織資料佈局，如計算一種新的排列順序。

大多數現代計算機使用儲存層級，其每一層級作為下一層的快取。儲存層級有兩個主要特徵。首先，較高層級尺寸也會大，接收處理器指令較慢，擁有較慢的訪問時間。第二，不同儲存級別之間，資料存在於大的塊中。格網初始存在於最高級別中，典型的如硬碟。應用訪問時格網某一部分將被轉移到較低級別的大分塊中，如主存。當有快取錯失發生的時候，兩個相鄰級別之間轉移就會執行。快取錯失次數依賴於原始格網在儲存空間中的佈局與應用訪問模式。

    格網布局是頂點與三角形的線性順序。構建一個圖，其中頂點代表格網中的資料單元。如果頂點代表的資料單元有可能在執行時被連續訪問，那麼兩個頂點之間存在一條邊。
     

對於單解析度格網布局，對映格網頂點與邊到圖的頂點與邊上。一個無向圖 的頂點佈局是頂點到位置的一一對映， ，目標是找到一種對映 ，使得格網訪問過程中最小化快取錯失數量。

格網布局有兩種佈局型別：頂點佈局與三角形佈局。而三角形佈局可被看成是頂點佈局的對偶圖，因為通過依賴三角形最大或最小頂點索引來排序三角形，將確保三角形佈局與頂點佈局相容。

為計算層次的佈局，可建立一個圖來獲取對層次的快取連貫訪問模式。在圖中增加額外的邊來獲得層次中的空間區域性關係與父子聯絡（Yoon, S.-E., Manocha,  2005）。

父子結點之間的聯絡。一旦層次中某一結點被訪問，有很大的可能性緊接著訪問其父結點與子結點。比如，VH中結點的頂點劈分啟用其子結點，兩個兄弟結點的邊摺疊操作啟用它們的父結點。

同一層次頂點之間空間區域性相關性。當一個結點被訪問時，其鄰近區域的其它結點有很大可能性被馬上訪問的。比如，兩個物體的碰撞和聯絡發生在小的格網區域性區域中。因此，如果BVH中一個結點被啟用，其它鄰近區域中的結點可能馬上被訪問。

5.5 本章小結

GPU專門為圖形渲染設計的，具有超長流水線與平行計算等主要特徵，運算速度越來越快，同時，在頂點級和畫素級還提供了靈活的可程式設計特性以及支援繪製到紋理等功能。因此，本章首先介紹了GPU特點與其支援下的圖形渲染流程之後，提出採用GPU繪製到紋理功能，獲取上幀三維模型成像資訊，進行可見性判斷，再把剔除視見體之外與被遮擋物體後剩餘的三維模型交給圖形流水線的方法，從而能節約計算時間，加快顯示速度。

針對過大或不符尺寸的紋理導致GPU因視訊記憶體不足而頻繁交換的問題，介紹Mipmap技術與Clipmap技術，既能保證比較快速的紋理查詢速度，又能有效解決硬體的儲存限制和載入頻寬的瓶頸。

指出在幾何資料處理過程中為避免CPU使用率達到上限，首先應該保證GPU足夠的三角形吞吐量。其次，快取在大多數GPU上是可用的，當使用FIFO頂點快取在最大程度上重複使用頂點時，將有利於提高模型格網的渲染速度。因此，介紹了迭代切割與MLA兩種方法以產生模型格網的渲染順序，生成的幾何資料佈局結果儘可能保留了格網區域性性並保證了頂點重用，還配合了上一章介紹的視點相關的實時有選擇性細化方法，能進一步提升大資料量場景繪製的速度。