給定兩個單詞（beginWord 和 endWord）和一個字典 wordList，找出所有從 beginWord 到 endWord 的最短轉換序列。轉換需遵循如下規則：

每次轉換隻能改變一個字母。 轉換過程中的中間單詞必須是字典中的單詞。 說明:

• 如果不存在這樣的轉換序列，返回一個空列表。
• 所有單詞具有相同的長度。
• 所有單詞只由小寫字母組成。
• 字典中不存在重複的單詞。
• 你可以假設 beginWord 和 endWord 是非空的，且二者不相同。

示例 1:

輸入:
beginWord = "hit",
endWord = "cog",
wordList = ["hot","dot","dog","lot","log","cog"]

輸出:
[
  ["hit","hot","dot","dog","cog"],
  ["hit","hot","lot","log","cog"]
]
 

示例 2:

輸入:
beginWord = "hit"
endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]

輸出: []

解釋: endWord "cog" 不在字典中，所以不存在符合要求的轉換序列。

Dijkstra演算法：演算法執行過程中，維持一個數組（最小優先佇列），陣列中記錄起點到每個節點的最短路徑

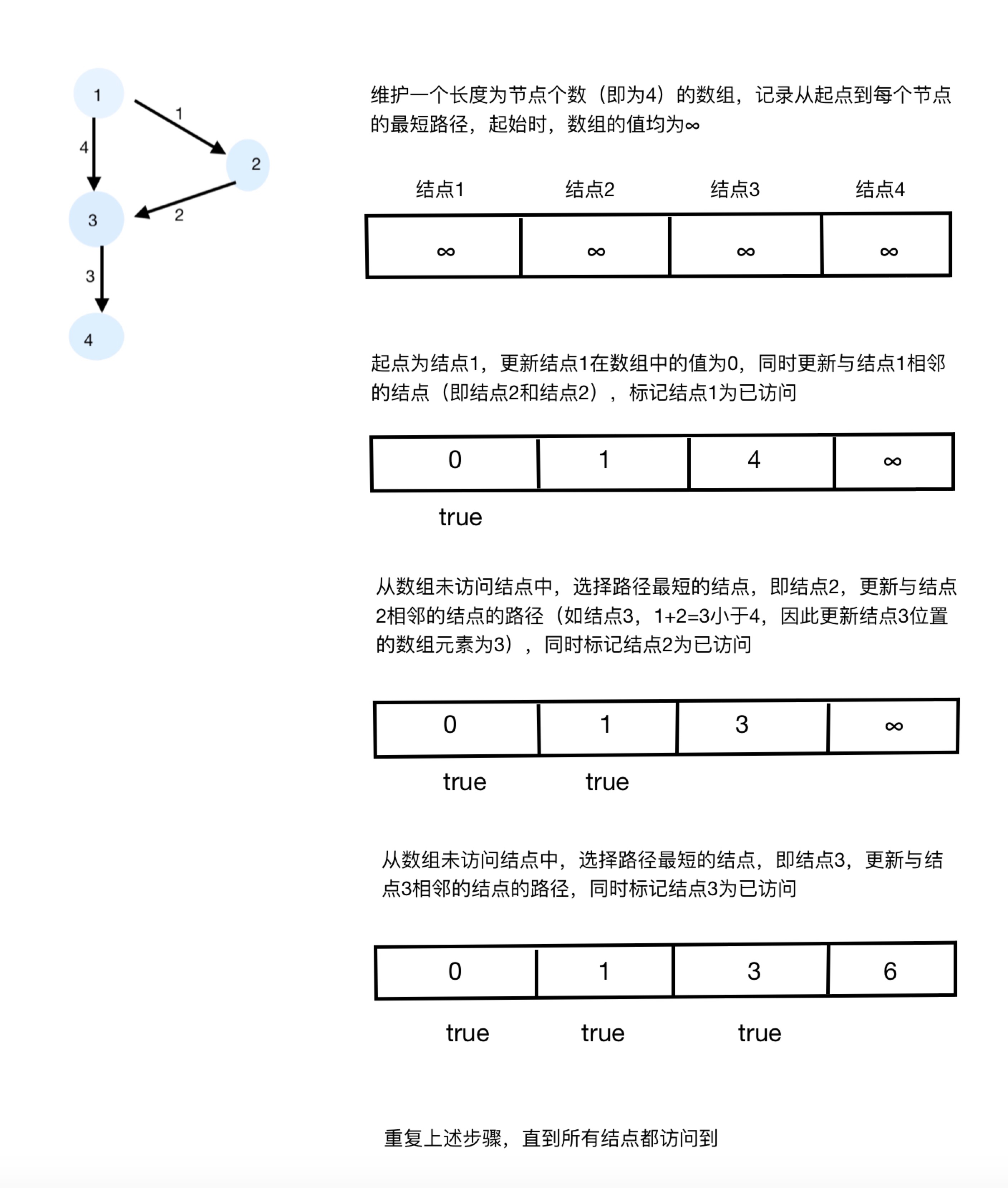
在這道題中（相當於每條邊權值均為1的有向圖），用Map記錄單詞字典中每個單詞至beginWord的最短路徑（即beginWord最少需要經過多少次才能轉換為字典中的每個單詞）

同時，在Dijkstra演算法計算最短路徑的過程中，用Map> relation記錄單詞字典中每個單詞的父節點（前一單詞）

計算完單詞字典中每個單詞的父節點（前一單詞）後，用深度優先遍歷，從endWord開始倒推出最短轉換路徑

注意：在Dijkstra演算法計算過程中，由於需要每次從未訪問的結點中求出最短路徑最小的結點，以更新周圍直接相連的結點，需要最小優先佇列來每次獲取當前路徑最短的結點，但這個題中，由於每條邊的權值均為1，因此可按照訪問到的順序將單詞放入佇列中，按照訪問順序取出的單詞，一定是當前未訪問結點的最短路徑，可提高效率。

Java程式碼：

class Solution {
    public List<List<String>> findLadders(String beginWord, String endWord, List<String> wordList) {
        /**
         * Dijkstra演算法
         * 1.用Map<String, Integer>維護每個元素到起點的長度，初始為∞
         * 2.用Map<String, List<String>>維護每個節點最短路徑的前一節點
         */
        Queue<String> queue = new java.util.concurrent.LinkedBlockingQueue<>();
        Map<String, Integer> dis = new HashMap<>();
        Map<String, List<String>> relation = new HashMap<>();

        dis.put(beginWord, 0);
        queue.add(beginWord);
        while(!queue.isEmpty()){
            // 獲取未訪問節點中，路徑最短的節點，所有邊的權重為1
            String str = queue.poll();
            int minPath = dis.get(str);

            // 更新與未訪問節點中路徑最短節點相鄰節點的最短路徑，同時記錄節點的最短路徑前一節點
            for(String key: wordList){

                // 判斷兩個節點是否相鄰
                int k = 0;
                for(int i = 0; i < key.length(); i++){
                    if(str.charAt(i) != key.charAt(i))
                        k++;

                    if(1 < k)
                        break;
                }
                // 相鄰節點，更新最短路徑，同時記錄節點的最短路徑前一節點
                if(1 == k){
                    if(null == relation.get(key) || null == dis.get(key) || minPath+1 < dis.get(key)){
                        List<String> re = new ArrayList<>();
                        re.add(str);
                        relation.put(key, re);
                    } else {
                        if(minPath+1 == dis.get(key))
                            relation.get(key).add(str);

                    }
                    if(!dis.containsKey(key))
                        queue.add(key);
                    dis.put(key, Math.min(minPath+1, null == dis.get(key) ? Integer.MAX_VALUE : dis.get(key)));
                }
            }

            // 剔除已訪問過節點
            dis.remove(str);
            wordList.remove(str);
        }

        List<List<String>> res = new LinkedList<>();
        LinkedList<String> tmp = new LinkedList<>();
        tmp.addFirst(endWord);
        dfs(endWord, tmp, relation, res, beginWord);

        return res;
    }
    private void dfs(String cur, LinkedList<String> tmp, Map<String, List<String>> relation, List<List<String>> res, String beginWord){
        if(cur.equals(beginWord)){
            res.add(new LinkedList<>(tmp));
            return;
        }
        if(!relation.containsKey(cur))
            return;

        List<String> pre = relation.get(cur);
        for(int i = 0; i < pre.size(); i++){
            cur = pre.get(i);
            tmp.addFirst(cur);
            dfs(cur, tmp, relation, res, beginWord);
            tmp.removeFirst();
        }
    }
}