最近研究二叉樹，比較經典的樹就是哈夫曼樹了，所以研究一下它的構建以及哈夫曼編碼，惡補一下資料結構的知識。

有一段密文：aabbccabcacb，解析為電碼傳輸，只能為0、1來表示
例如
a 0
b 1
c 01
d 10
… …
那麼aabc….可以表示為00101，但是在解析的時候發現0 01 10可以出現混亂，001可以解析為 ac 或者 aab，這樣就會導致資料不唯一。因此可以用二叉樹來保證資料唯一。

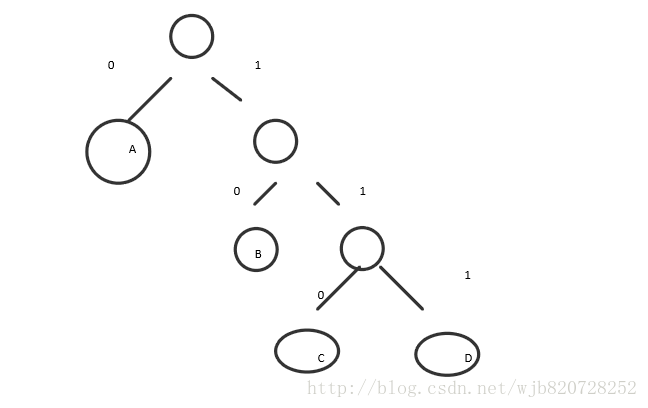
左邊用0表示，右邊用1表示，那麼abcd的編碼如下：
A 0
B 10
C 110
D 111
aabc….
可以表示為0010110，在解析的時候就不會出現混亂，因為資料是唯一表示的。

那麼問題又來了，如果a編碼出現的次數是1次，b編碼的出現次數是1次，c出現次數是10000
那麼aabc的資料長度：1*1 +1*1+2*1+3*10000+…
那麼如何進行優化，是這個編碼的長度最短？可以通過調整數節點的位置，例如下：

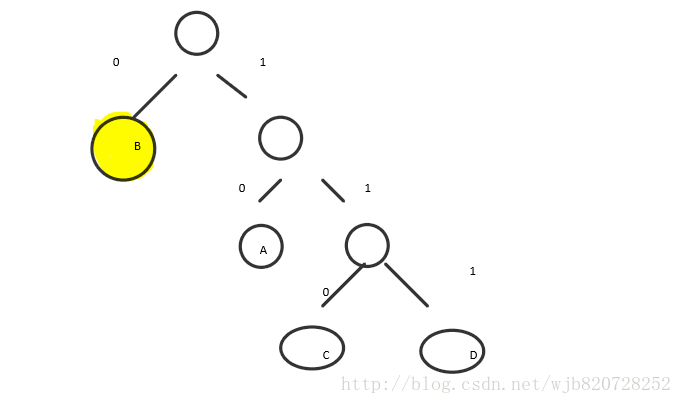
左邊用0表示，右邊用1表示，那麼abcd的編碼如下：
B 0
A 10
C 110
D 111
那麼aabc…的編碼將會變成
2*1+2*1+1*10000+…
這樣就可以使得在保證編碼資料唯一的情況下，編碼長度最小。這就是一個哈夫曼編碼，這課樹就是哈夫曼樹

哈夫曼樹定義：指對於一組帶有確定權值的葉節點，構造的具有最小帶權路徑長度的二叉樹

Wpl=(w1 * l1+w2*l2 + ·····)

////////////////////////////////////////////////////////////////////////////////////////////////////////////////
構造哈夫曼樹：
步驟：先對陣列A排序，後選擇前兩個最小的值作為左右節點，它們之和是其根節點（父節點node），node入陣列A，直到陣列A只剩下一個元素。

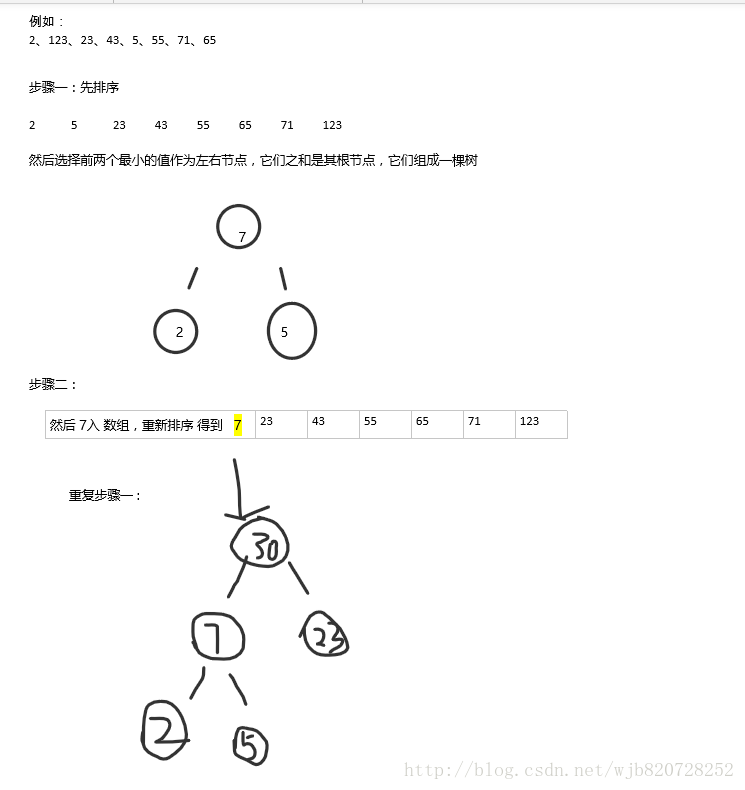
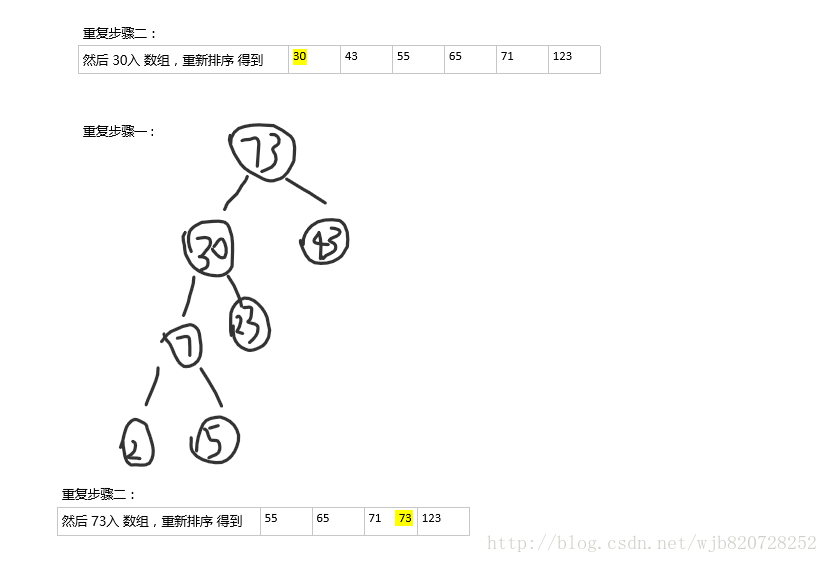
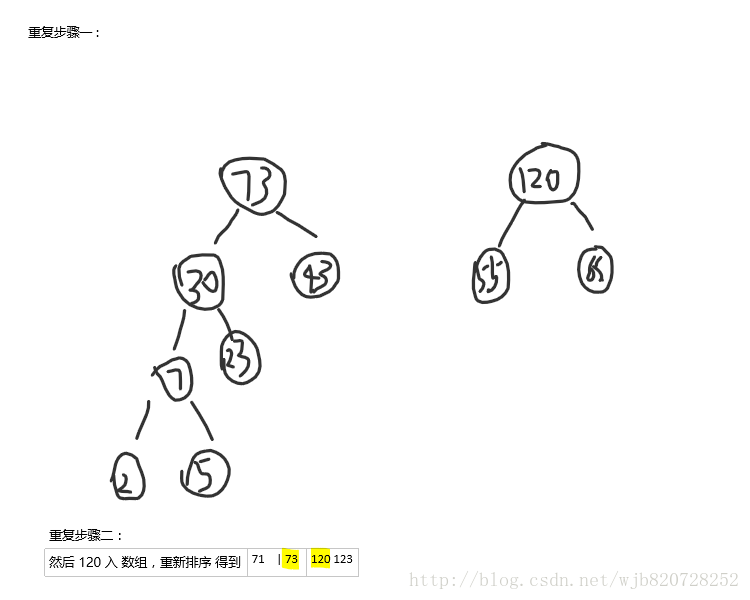
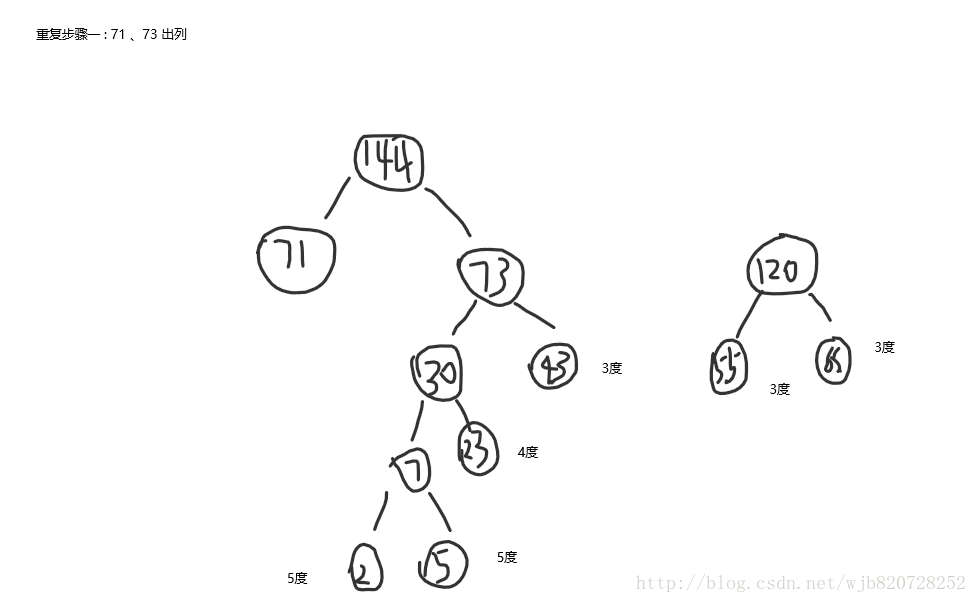
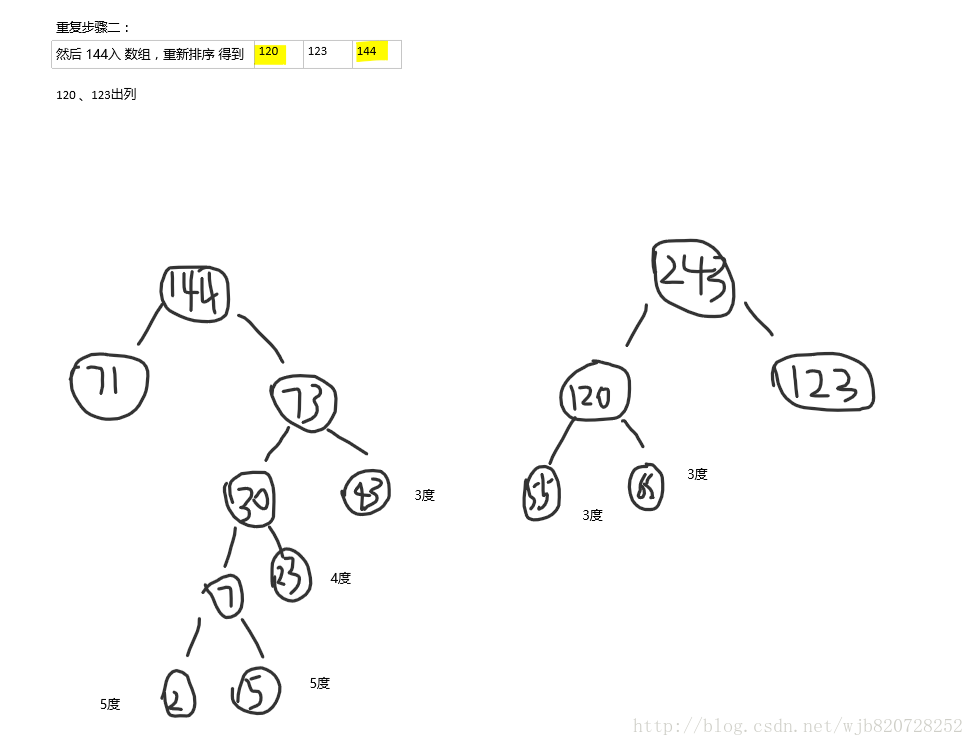
結束迴圈
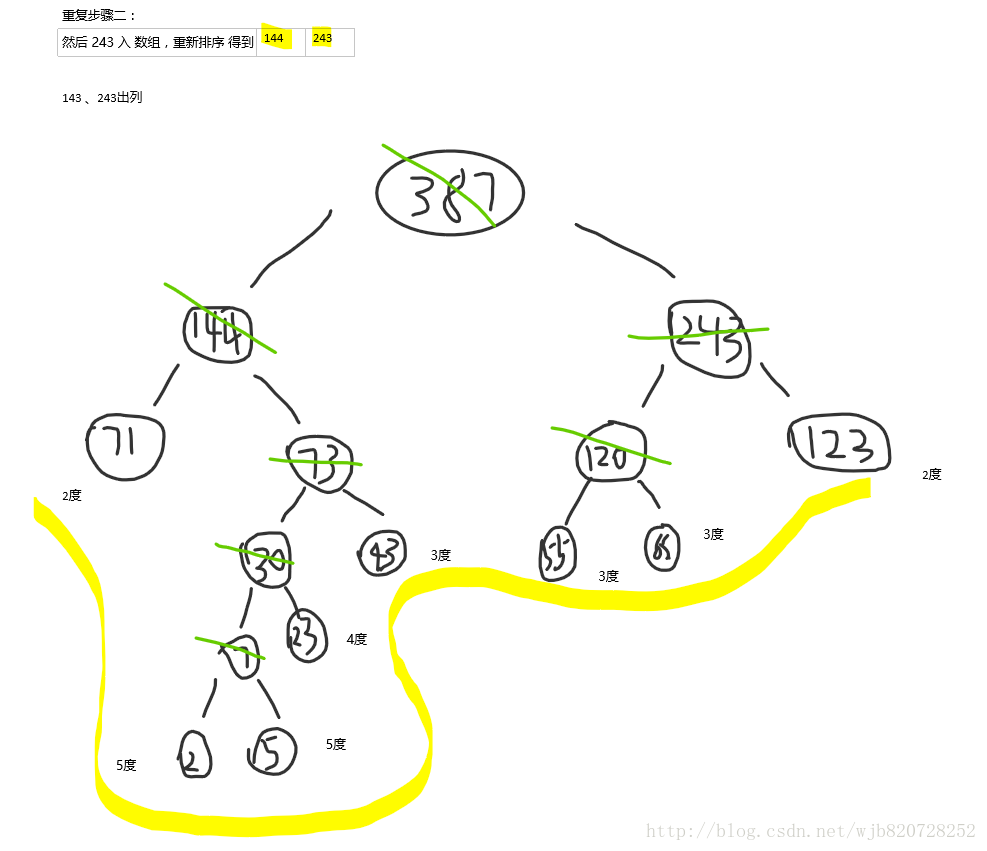
2 5 23 43 55 65 71 123

總度數：
Sum=2*5+5*5+23*4+43*3+55*3+65*3+71*2+123*2
=10+ 25+ 92 +129 +165 +195 +142 + 246
=1004度

程式碼實現：
/**
 * 類節點
 * @author breeze
 *
 * @param <E>
 */
 

class TreeNode<E> implements Comparable<TreeNode<E>>{
    E data;
    int weight;
    TreeNode<E>left;
    TreeNode<E>right;
    TreeNode<E> parent;
    public TreeNode(E data,int weight) {
        this.data = data;
        this.weight=weight;
        left=null;
        right=null;
        parent=null;
    }
}

/**
 * 建立哈夫曼樹
 * @param list
 */
public void createHafumanTree(ArrayList<TreeNode<Integer>> list){
    while(list.size()>1){
        Collections.sort(list);
        TreeNode<Integer> left =list.remove(0);
        TreeNode<Integer> right =list.remove(0);
        TreeNode<Integer> parent =new TreeNode<Integer>(data,left.weight+right.weight);
        parent.left=left;
        parent.right=right;
        left.parent=parent;
        right.parent=parent;
        list.add(parent);
    }
    if(!list.isEmpty()){
        this.root=list.get(0);
    }else{
        this.root=null;
    }
}

那麼哈夫曼編碼怎麼獲取到？
這裡使用的方法是先搜尋樹，查詢到要編碼的節點位置，然後通過判斷父節點的分支方向並
使用棧來儲存結果
步驟：
1、通過搜尋樹找到節點（這裡使用廣度優先搜尋）。
2、迴圈判斷該節點父節點是否為空
3、如果該節點是左分支則入棧0，如果其是右分支則入棧1，向上移動，迴圈進入步驟二。

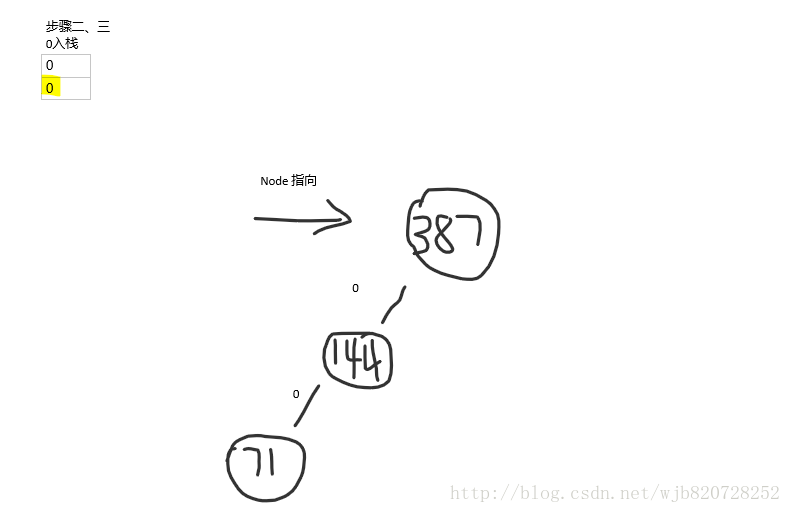
例如：查詢 71 節點的哈夫曼編碼

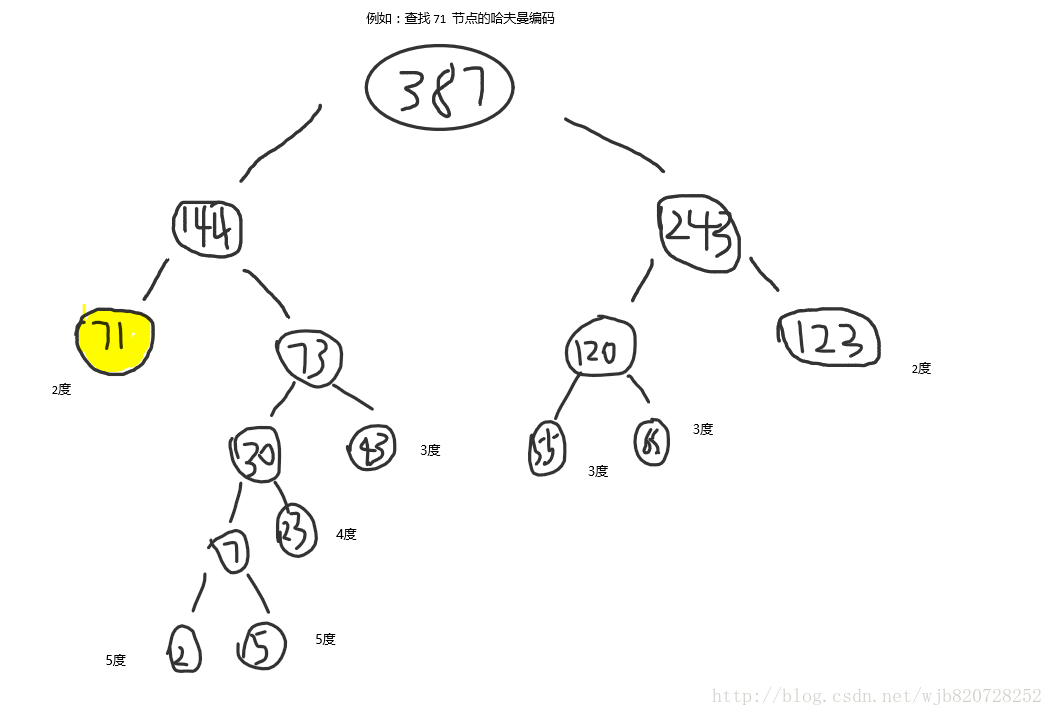
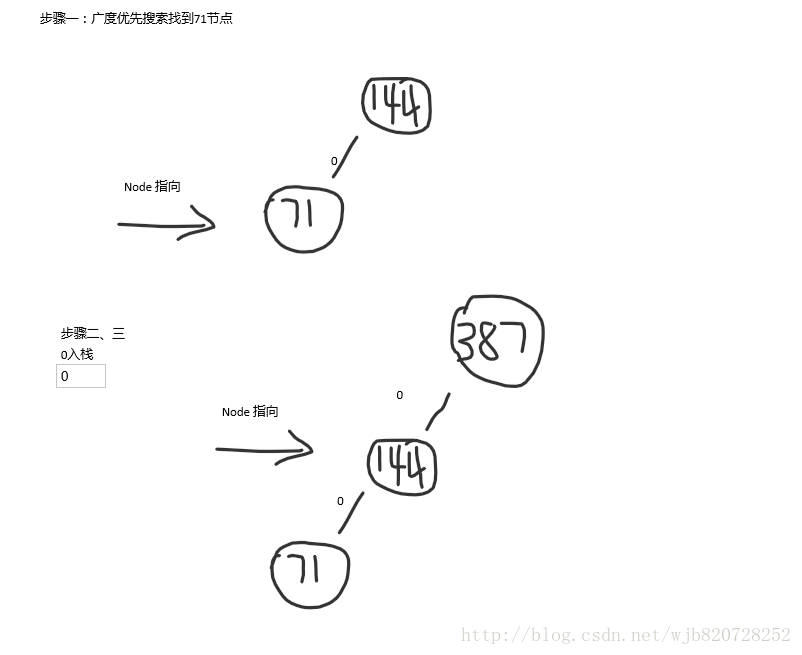
步驟二：判斷其父節點給null，則直接退出

最後然後遍歷棧，得到的就是哈夫曼編碼了

71的哈夫曼編碼是 00

具體程式碼如下：

    /**
     * 普通樹查詢
     * 廣度優先遍歷、當然還有前、中、後序遍歷樹（遞迴或者棧實現）
     * @param data
     * @return
     */
    public TreeNode<Integer> sreachNode(int data){
        TreeNode<Integer> result=null;
        if(null==root){
            return null;
            }else{
            LinkedList<TreeNode<Integer>> list =new LinkedList<>();
            list.addFirst(root);
            while(!list.isEmpty()&&result==null){
                TreeNode<Integer> node =list.pollFirst();
                if(node.data==data)
                    result=node;
                if(node.left!=null){
                    list.addLast(node.left);
                }
                if(node.right!=null){
                    list.addLast(node.right);
                }
            }
        }
        return result;
    }
    /**
     * 棧前序遍歷
     * @param node
     */
    public void preStackLook(TreeNode<Integer> node){
        if(null==node){
            return ;
        }else{
            Stack<TreeNode<Integer>> stack=new Stack<>();
            stack.push(node);
            while(!stack.isEmpty()){
                node=stack.pop();
                System.out.print(node.data +"   ");
                if(null!=node.right)
                    stack.push(node.right);
                if(null!=node.left)
                    stack.push(node.left);
            }
        }
    }
    /**
     * 遞迴前序遍歷
     * @param root
     */
    public void preOrderLook(TreeNode<Integer> root){
        if(null==root){
            return ;
        }
        System.out.print(root.data+"    ");
        preOrderLook(root.left);
        preOrderLook(root.right);
    }

    /**
     * 遞迴中序遍歷
     * @param root
     */
    public void midOrderLook(TreeNode<Integer> root){
        if(null==root){
            return ;
        }
        midOrderLook(root.left);
        System.out.print(root.data+"    ");
        midOrderLook(root.right);
    }

    /**
     * 遞迴前後序遍歷
     * @param root
     */
    public void breforeOrderLook(TreeNode<Integer> root){
        if(null==root){
            return ;
        }
        breforeOrderLook(root.left);
        breforeOrderLook(root.right);
        System.out.print(root.data+"    ");
    }
    /**
     * 獲取哈夫曼編碼
     * @param data
     * @return
     */
    public String getCode(Integer data){
        TreeNode<Integer> node =sreachNode(data);
        String result="";
        if(node==null)
            return null;
        else{
            Stack<Integer> stack =new Stack<>();
            while(node.parent!=null){
                if(node.parent.left==node){
                    stack.push(0);
                }else{
                    stack.push(1);
                }
                node=node.parent;
            }
            for(;!stack.isEmpty();){
                result+=stack.pop();
            }
        }
        return result;
    }

總結：以上就是哈夫曼樹的由來、建立、遍歷、獲取哈夫曼編碼等的過程了。比較簡單，記錄一下，方便以後檢視