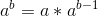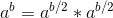Pat甲級題目刷題分享+演算法筆記提煉 ---------------第一部分 基本資料操作與常用演算法
一、演算法筆記提煉
· 數學相關
1. 最大公約數+最小公倍數(只需要記住 定理即可)
gcd(a,b) = gcd(b,a%b); 意思是:a與b的最大公約數 即 b與a%b的最大公約數 而 0 與數a的最大公約數為數a,自然遞迴邊界很容易得知
int gcd(int a,int b) {
if (b==0) {
return a;
}
return gcd(b,a%b);
}最小公倍數就較為簡單,是基於最大公約數
int lcm(int a,int b){
int m=gcd(a,b);
if(m==0) return 0;
return a*b/m;
}2.素數的判斷(素數表的構建,用篩選法能夠很大程度降低時間複雜度)
不能整除1和自身之外的其他數的自然數,自然數1除外,而sqrt(n)就是n的中介數,如果一個數x>sqrt(n),x!=n且能被n整除,那麼商一定是小於sqrt(n),因此只需要遍歷2-sqrt(n)即可
bool is_prime(int n){ if(n==0||n==1) return false; int s=(int)sqrt(1.0*n); for(int i=2;i<=s;i++){ if(n%i==0) return false; } return true; }
配合上述判斷素數的方法O(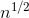
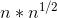
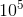
const int maxn = 100;
int prime[maxn], pNum = 0; //prime儲存素數, pNum是指素數個數
bool p[maxn] = {0}; //p[i]代表i是否為素數
void Find_Prime() {
for (int i = 0; i <= maxn;i++) {
if (is_prime(i)) {
p[i] = true;
prime[pNum++] = i;
}
}
}更為快速的構建素數表的方法,名為素數篩選法,主要步驟就是篩,因為非素數均等於小於其的某兩個數的積,演算法從小到大列舉每一個數,對於每一個素數,篩去其所有倍數,沒有被前面步驟所篩去的數即為素數.
const int maxn = 100;
int prime[maxn], pNum = 0; //prime儲存素數, pNum是指素數個數
bool p[maxn] = {0}; //p[i]代表i是否為素數
void Find_Prime() {
for (int i = 2; i <= maxn;i++) {
if (p[i]==false) {
prime[pNum++] = i; //代表i沒有被篩去
for (int j = i + i; j <= maxn;j+=i) {//把後面i的倍數全部篩去
p[j] = true;
}
}
}
}這樣此演算法就用不到判斷n是否為素數的函數了,時間複雜度為:O(
3.質因子分解(顧名思義:將一個正整數寫成一個或多個質數的乘積。如:180=2*2*3*3*5) 另言 也就是說,大於2的任何正整數都是某個素數的倍數,若為1倍,則其為素數,再回顧上述的素數篩選法,是否更有所啟發呢.
還是回到sqrt(n)這個關鍵數,定理:一個數的質因子要麼全部小於sqrt(n),要麼只有一個大於sqrt(n),定理很好理解,因為不可能出現兩個大於sqrt(n)的質因子
①演算法思想,列舉1~sqrt(n)的所有質數p,判斷其是否為n的因子.如果是n/=p;
如果列舉完後n>1,則n為最後一個質因子,且n一定大於sqrt(n)
上程式碼:
#include<iostream>
using namespace std;
//此處需要用到上述的素數表
struct factor {
int x, cnt;
}fac[10];
int main() {
Find_Prime();
int n;
cin >> n;
int sqr = (int)sqrt(1.0*n);
int num = 0;//記錄不同因子個數
for (int i = 0; i<pNum&&prime[i] <= sqr; i++) {
if (n%prime[i] == 0) {
fac[num].x = prime[i];
fac[num].cnt = 0;
while (n%prime[i] == 0) {//計算出prime[i]這個質因子的個數
fac[num].cnt++;
n /= prime[i];
}
num++;
}
if (n == 1) break; //及早結束迴圈
}
if (n != 1) {
fac[num].x = n;
fac[num++].cnt = 1;
}
return 0;
}
.大數相關(即計算機無法表示的數,如:容易溢位的大數的加減,分數的加減乘除以及化簡)
1.大數的儲存
struct bign{
int d[1000]; //越低位儲存的下標越小,如235 則d[0]=5,d[1]=3,d[2]=2
int len;
bign(){memset(d,0,sizeof(d));len=0;}
};一般在輸入大整數時是字串的形式,所以需要將字串轉為bign結構體
bign change(char str[]){
bign b;
b.len=strlen(str);
for(int i =0;i<b.len;i++){
b.d[i]=str[b.len-i-1]-'0';
}
return b;
}2.大數比較大小
int compare(bign b1,bign b2){
if(b1.len>b2.len)return 1;
else if(b1.len<b2.len) return -1;
for(int i=b1.len-1;i>=0;i--){
if(b1.d[i]>b2.d[i]) return 1;
else if(b1.d[i]<b2.d[i]) return -1;
}
return 0;
}3.大數的加法
bign add(bign a,bign b){
bign c;
int carry=0;
//從低位開始加 因為分配好了足夠大小的空間,兩者未對齊部分有一方已經預設為0
for(int i=0;i<a.len||i<b.len;i++){
int sum=a.d[i]+b.d[i]+carry;
c.d[c.len++]=sum%10;
carry=sum/10;
}
if(carry!=0) c.d[c.len++]=carry;
return c;
}
4.大數的減法
bign sub(bign a,bign b){ //預設要求a>=b
bign c;
for(int i=0;i<a.len||i<b.len;i++){
if(a.d[i]<b.d[i]){//不夠減
a.d[i+1]--;
a.d[i]+=10;
}
c.d[c.len++]=a.d[i]-b.d[i];
}
//減法很容易出現 高位為0的情況,所以減完後需要去除多餘的0,修正長度
while(c.len>=2&&c.d[c.len-1]==0){
c.len--;
}
return c;
}5.大數與int變數的乘法
演算法思想:始終將int變數看作一個整體,與大數每一位相乘,結果的個位作為該位結果,其餘當作進位
bign multi(bign a,int b){
bign c;
int carry=0;
for(int i=0;i<a.len;i++){
int sum=a.d[i]*b+carry;
c.d[c.len++]=sum%10;
carry=sum/10;
}
while(carry!=0){
c.d[c.len++]=carry%10;
carry/=10;
}
return c;
}那麼大數與大數 A*B的演算法思想即為將B的陣列d每一位當作b傳入函式multi之後再求和即可 。
6.大數與int變數的除法
演算法思想:1234/7 ->1/7商0餘數1 ,12/7商1餘5,53/7商7餘4,44/7商6餘2
bign divide(bign a,int b,int &r){
bign c;
c.len=a.len;
//從高位開始除
for(int i=a.len-1;i>=0;i--){
r=a.d[i]+r*10;
c.d[i]=r/b;
r=r%b;
}
while(c.len>=2 && c.d[c.len-1]==0){
c.len--;
}
return c;
}.快速冪(俗稱二分冪)減少遞迴次數,防止棧溢位
①如果b是奇數,
②如果b是偶數,
所以在log(b)次後就可以將b變為0,任何數的0次方為1
tyepdef long long LL;
//求a^b % m
LL binaryPow(LL a,LL b,LL m){
if(b==0) return 1;
if(b%2==0){
LL temp=binaryPow(a,b/2,m);
return temp*temp%m;
}else{
return a*binaryPow(a,b-1,m);
}
}.動態規劃
貪心與分治均不屬於動態規劃,動態規劃十分容易理解,就是不斷的做最優小決策,簡單來將就是將問題分解為多個重疊的小問題,求解小問題的最優解.何為重疊呢,即兩個問題求解過程中,有公共解部分,但公共解不一定是最優解
1.數塔問題
求從頂層走到底層的路徑上的數字和的最大值,上圖只畫了一部分,強調的是5-8-7,5-3-7可能是會走重路,因為會重複去計算從7出發再去底層時候的最優解。所以就會想到dp[i][j]代表第i層第j個數到達底層的最大數字和.顯然dp[1][1]為最終要求解的值
dp[1][1]=max(dp[2][1],dp[2][2])+f[1][1] //其中f[i][j]代表第i層第j個數的數值
就有了,推導式:dp[i][j]=max(dp[i+1][j],dp[i+1][j+1])+f[i][j];
邊界就很容易知道,最底層的dp[n][j]=f[n][j]
#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn = 1000;
int f[maxn][maxn], dp[maxn][maxn];
int main() {
int n;
scanf("%d",&n);
for (int i = 1; i <= n;i++) {
for (int j = 1; j <=i;j++) {
scanf("%d",&f[i][j]);
}
}
//邊界
for (int i = 1; i <= n; i++) { dp[n][i] = f[n][i]; }
//從下往上,從n-1層開始
for (int i = n - 1; i >= 1;i--) {
for (int j = 1; j <= i;j++) {
dp[i][j] = max(dp[i+1][j],dp[i+1][j+1])+f[i][j];
}
}
printf("%d",dp[1][1]);
return 0;
}
2.最長不下降子序列(可以不連續)LIS
A={1,2,3,-1,-2,7,9} 它的最長不下降子序列是:{1,2,3,7,9}
dp[i]代表以A[i]結尾的最長不下降子序列
所以迴圈到A[i]時,就要以此與j>=1 && j<i的數進行比較,若可以排在其後則更新dp[i]=dp[j]+1,若不能排在其後,則dp[i]=1
所以有推導式:dp[i]=max(1,dp[j]+1); j=1,2,3....i-1 && A[j]<=A[i]
邊界:dp[i]=1;//每個元素自成一個序列
#include<cstdio>
#include<algorithm>
#include<vector>
using namespace std;
const int maxn = 1000;
int dp[maxn];
int A[maxn];
int main() {
int n;
scanf("%d",&n);
for (int i = 1; i <= n;i++) {
scanf("%d",&A[i]);
dp[i] = 1;//邊界
}
int ans=0;
for (int i = 1; i <= n;i++) {
for (int j = 1; j < i;j++) {
if (A[j]<=A[i] && dp[j]+1>dp[i]) {
dp[i] = dp[j]+1;
}
}
ans = max(ans,dp[i]);
}
printf("%d",ans);
//知道以誰結尾式最長非下降子序列後,只需要根據其下標往前找小於等於它的數即可
return 0;
}
3.最大連續子序列和
給定一個數字序列 A1,A2,。。。An求 1<=i<=j<=n 使得Ai+.....+Aj最大
同理認為dp[i]代表以A[i]結尾的最大和,那麼每次遍歷時候,dp[i]=max(A[i],dp[i-1]+A[i]);
而dp[i]得深層含義就是,A[p]+A[p+1]+...A[i]和最大,仔細斟酌就會很容易理解哦。
#include<cstdio>
#include<algorithm>
#include<vector>
using namespace std;
const int maxn = 10010;
int dp[maxn];
int A[maxn];
int main() {
int n;
scanf("%d",&n);
for (int i = 0; i <n;i++) {
scanf("%d",&A[i]);
}
//邊界
dp[0] = A[0];
int ans = 0;
int index = 0;
for (int i = 0; i < n;i++) {
dp[i] = max(dp[i-1]+A[i],A[i]);
if (dp[i] > ans) {
index = i;
ans = dp[i];
}
}
printf("%d\n",ans);
//下述式尋找最大得連續子序列,從後往前輸出
int sum = 0;
for (int j = index; j >=0;j--) {
sum += A[j];
if (sum == ans) { //這個一定要在前,一旦等於即退出迴圈
printf("%d", A[j]);
break;
}
else if (sum < ans) {
printf("%d ",A[j]);
}
}
return 0;
}
4.最長迴文串
給定一個字串S,求S的最長迴文子串的長度
dp[i][j]表示S[i]至S[j]是否為迴文子串,dp[i][j]=0不是,dp[i][j]=1是迴文子串
兩種情況:
①S[i]==S[j],則只要S[i+1]至S[j-1]是迴文子串則其是迴文子串,否則不是
②S[i]!=S[j]則不是迴文子串
dp[i][j]=dp[i+1][j-1],S[i]==S[j] or = 0 ,S[i]!=S[j]
邊界:dp[i][i]=1,dp[i][i+1]=(S[i]==S[j]?1:0)
演算法思想,從迴文子串的長度出發考慮,即先列舉子串的長度L,再列舉左端點i,那麼右端點i+L-1就自然確定了。
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn = 1010;
char S[maxn];
int dp[maxn][maxn];
int main(){
gets_s(S);
int len = strlen(S), ans = 1;
memset(dp,0,sizeof(dp));
for (int i = 0; i < len; i++) { //邊界
dp[i][i] = 1;
if (i < len - 1 && S[i]==S[i+1]) {
dp[i][i + 1] = 1;
ans = 2;
}
}
for (int L = 3; L <= len; L++) {
for (int i = 0; i + L - 1 < len;i++) {
int j = i + L - 1;
if (S[i]==S[j] && dp[i+1][j-1]==1) {
dp[i][j] = 1;
ans = L;
}
}
}
printf("%d\n",ans);
return 0;
}
5.最長公共子序列 LCS
給定兩個字串(或者數字序列) A和B,求一個字串,使得這個字串是A和B的最大公共部分 子序列可以不連續
令dp[i][j]表示字串A的i號位和字串B的j號位之前的LCS長度(下標從1開始),dp[4][5]表示sads和admin的LCS長度
可以根據A[i]和B[j]的情況。分為兩種決策:
①若A[i]==B[j],則字串A與字串B的LCS增加了1位,即有dp[i][j]=dp[i-1][j-1]+1;
②若A[i]!=B[j],則dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
邊界:dp[i][0]=dp[0][j]=0;
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn = 1000;
char A[maxn], B[maxn];
int dp[maxn][maxn];
int main() {
A[0] = ' '; B[0] = ' ';
scanf("%s", A + 1);
scanf("%s", B + 1);
int len_A = strlen(A);
int len_B = strlen(B);
for (int i = 0; i < len_A; i++) {
dp[i][0] = 0;
}
for (int i = 0; i < len_B; i++) {
dp[0][i] = 0;
}
int LCS = 0, k = 0;
char res[maxn];
for (int i = 1; i < len_A; i++) {
for (int j = 1; j < len_B; j++) {
if (A[i] == B[j]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
}
else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
}
printf("%d", dp[len_A - 1][len_B - 1]);
return 0;
}
如果想獲取到這個最長公共字串,就需要在上面的基礎上做一些特殊處理。
演算法思想為:首先記錄A與B相等字元在A中的下標index_A和B中的下標index_B,並且統計出相等字元的總數。同時用結構體陣列儲存上述這些資訊,之後遍歷結構體陣列,得出index_B從小到大且沒有相等的最大子陣列就是最終答案。
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn = 1000;
char A[maxn],B[maxn];
int dp[maxn][maxn];
struct Node
{
int index_A; //A與B相同的字元在A中的下標
int index_B; //A與B相同的字元在B中的下標
}nodes[maxn];
int main() {
A[0] = ' '; B[0] = ' ';
scanf("%s", A + 1);
scanf("%s",B+1);
int len_A = strlen(A);
int len_B = strlen(B);
for (int i = 0; i <= len_A; i++) {
dp[i][0] = 0;
}
for (int i = 0; i <= len_B; i++) {
dp[0][i] = 0;
}
int eq_num = 0,k=0;
char res[maxn];
for (int i = 1; i < len_A; i++) {
for (int j = 1; j < len_B; j++) {
if (A[i] == B[j]) {
eq_num++;
dp[i][j] = dp[i - 1][j - 1] + 1;
Node node;
node.index_A = i;
node.index_B = j;
nodes[k++] = node;
}
else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
}
if (eq_num == 0) {
printf("0");
return 0;
}
int LCS = 0;
Node pre_node=nodes[0];
for (int i = 1; i < eq_num;i++) {
if (nodes[i].index_B<pre_node.index_B) {
LCS = 0; //重新記錄最長公共序列的長度
res[LCS++] = A[nodes[i].index_A];
pre_node = nodes[i];
}
else if(nodes[i].index_B>pre_node.index_B &&
nodes[i].index_A!=pre_node.index_A) {
res[LCS++] = A[nodes[i].index_A];
pre_node = nodes[i];
}
if (LCS == dp[len_A-1][len_B-1]) break;
}
res[LCS] = '\0';
printf("%s", res);
return 0;
}
.揹包問題 (個人覺得揹包問題是一個動態規劃問題,用貪心策略雖然有時候有效,但貪心策略很難證明,因此很難認定用貪心策略得出的結果是全域性最優。但是我還是會分別展示貪心策略和動態規劃解法,因為貪心策略也是一種很常用的基本演算法,我還是很有良心的。)
1. 01揹包問題
有n件物品,每件物品的重量為w[i],價值為c[i]。現有一個容量為V的揹包,問如何選取物品放入揹包,使得揹包內物品的總價值最大。其中每件物品只有一件。
樣例:
5 8 //n=5,V=8
3 5 1 2 2 //w[i]
4 5 2 1 3 //c[i]
<1>動態規劃解法
令dp[i][v]表示第i件物品巧好裝入揹包中獲得的最大價值
對物品i的選擇策略有兩種:
①不放物品i,那麼就是指前i-1件物品恰好放入容量為v的揹包中獲得的最大價值 為dp[i-1][v]
②放物品i,那麼就是指前i-1件物品恰好放入容量為v-w[i]的揹包中所能獲取的最大價值dp[i-1][v-w[i]]
dp[i][v]=max(dp[i-1][v],dp[i-1][v-w[i]+c[i]]);
可以看出dp[i][v]只與dp[i-1][]相關,那麼可以列舉i從1到n,v從0到V
邊界:dp[0][v]=0
#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn=100;
const int maxv=1000;
int w[maxn],c[maxn],dp[maxn][maxv];
int main(){
int n,V;
scanf("%d %d",&n,&V);
for(int i=1;i<=n;i++){
scanf("%d",&w[i]);
}
for(int i=1;i<=n;i++){
scanf("%d",&c[i]);
}
//邊界
for(int v=0;v<=V;v++){
dp[0][v]=0;
}
for(int i=1;i<=n;i++){
for(int v=w[i];v<=V;v++){
dp[i][v]=max(dp[i-1][v],dp[i-1][v-w[i]]+c[i]);
}
}
int max=0;
for(int i=1;i<=n;i++){
if(dp[i][V]>max) max=dp[i][V];
}
printf("%d\n",max);
return 0;
}
<2>貪心策略解法
因為跟體積有關,所以每次選擇單位體積下價值最高的物品入揹包是當下最優的選擇。程式碼如下:
#include<cstdio>
#include<algorithm>
using namespace std;
struct Product
{
int w,c;
double unit;
};
const int maxn = 100; //物件上限
Product p[maxn];
bool cmp(Product p1,Product p2) {
if (p1.unit > p2.unit) return true;
return false;
}
int main(){
int n, V;
scanf("%d %d",&n,&V);
for (int i = 1; i <= n; i++) {
scanf("%d", &p[i].w);
}
for (int i = 1; i <= n;i++) {
scanf("%d",&p[i].c);
p[i].unit = (p[i].c*1.0) / p[i].w;
}
//排序
sort(p+1,p+n+1,cmp);
int i = 1, max = 0, remain_V = V;
while (i<=n) {
if (p[i].w <= remain_V) { //可以放入
remain_V -= p[i].w;
max += p[i].c;
}
i++;
}
printf("%d",max);
return 0;
}
2.完全揹包問題
有n種物品,每種物品的重量為w[i],價值為c[i]。現有一個容量為V的揹包,問如何選取物品放入揹包,使得揹包內物品的總價值最大。其中每種物品都有無窮件。
01揹包問題中每種物品的個數為一件,而完全揹包問題中每種物品的件數是無限的
同樣令dp[i][v] 代表第i種物品恰好放入揹包所獲取的最大收益
同樣對於第i種物品有兩種策略:
①第i種物品不放入 最大收益即為 dp[i-1][v]
②第i種物品放入,此時就和01揹包問題不一樣了,因為第i種物品不止一件,所以第i種物品可以放到v-w[i]<0為止。
狀態轉移方程為:dp[i][v]=max(dp[i-1][v],dp[i][v-w[i]]+c[i])
邊界:dp[0][v]=0
#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn=100;
const int maxv=1000;
int w[maxn],c[maxn],dp[maxn][maxv];
int main(){
int n,V;
scanf("%d %d",&n,&V);
for(int i=1;i<=n;i++){
scanf("%d",&w[i]);
}
for(int i=1;i<=n;i++){
scanf("%d",&c[i]);
}
//邊界
for(int v=0;v<=V;v++){
dp[0][v]=0;
}
for(int i=1;i<=n;i++){
for(int v=w[i];v<=V;v++){
dp[i][v]=max(dp[i-1][v],dp[i][v-w[i]]+c[i]);
}
}
int max=0;
for(int i=1;i<=n;i++){
if(dp[i][V]>max) max=dp[i][V];
}
printf("%d\n",max);
return 0;
}
.字串部分 KMP演算法(這裡就只是奉上 獲取next陣列的程式碼,因為KMP演算法思想講解比較繁瑣,如果有想要完整程式碼的可以留言,暫時就寫這麼多)
給定兩個字串text 和Pattern,判斷pattern是否時text的子串
const int maxn=1000;
int next[maxn];
void getNext(char s[],int len){
int j=-1;
next[0]=-1;
for(int i=1;i<len;i++){ //求解next[1]~next[len-1]
while(j!=-1 && s[i]!=s[j+1]){
j=next[j];
}
if(s[i]==s[j+1]){
j++;
}
next[i]=j;
}
}