1.一個滿二叉樹的定義是，所有的節點要麼有兩個子節點，要麼沒有子節點。定義B_n為：n個節點的滿二叉樹，對應的二叉樹數量。對稱的兩個樹分別計算。求證：B_n∈Ω（2ⁿ）

比如，B₁=1，B₃=1，B₅=2。

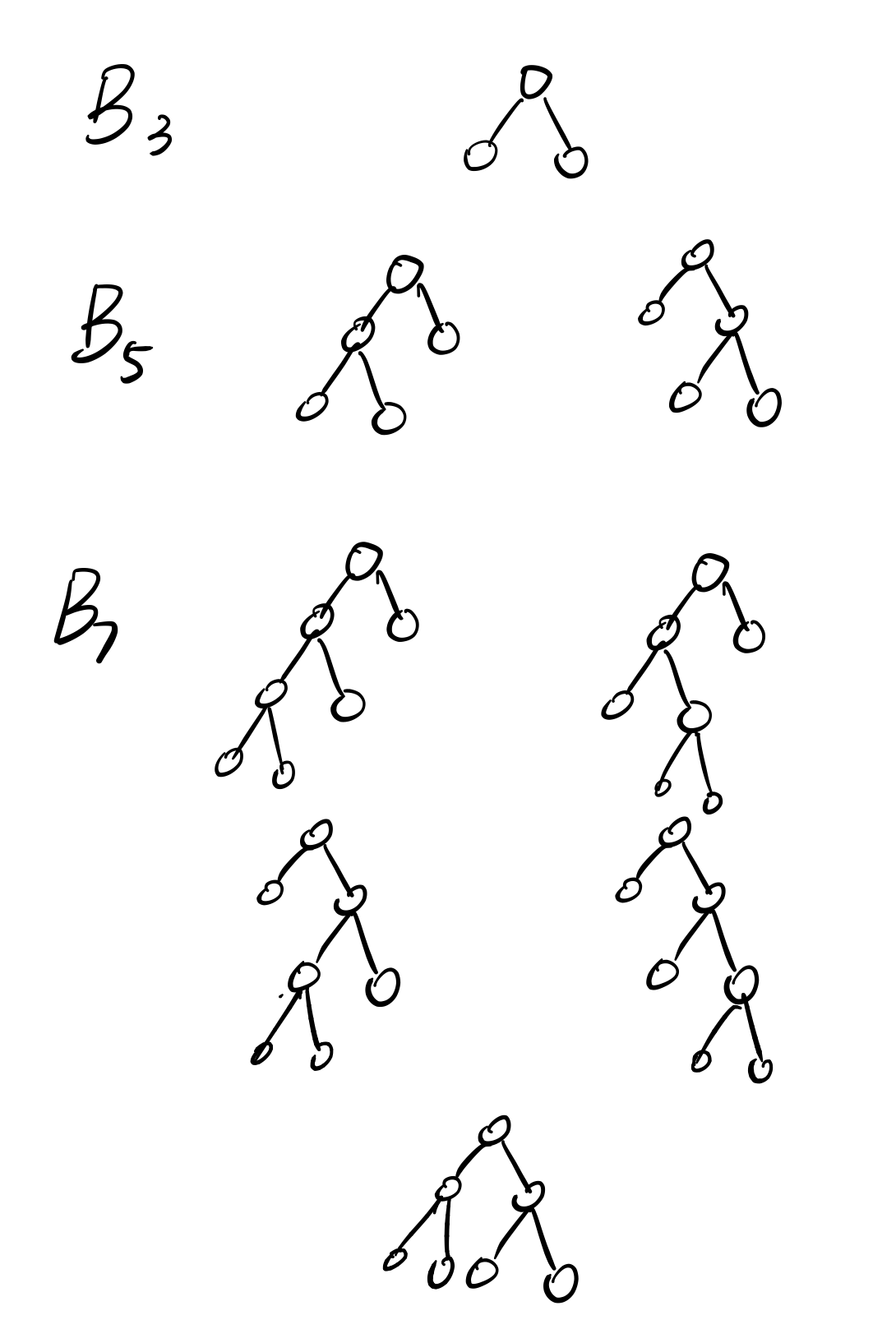
這題的關鍵在於求出Bn的遞推式。多畫幾次就能發現，實際上對於一顆B_n樹，包含的情況有一邊子樹為B₁，一邊子樹為B_n-2。依次類推可以得到如下遞推式：

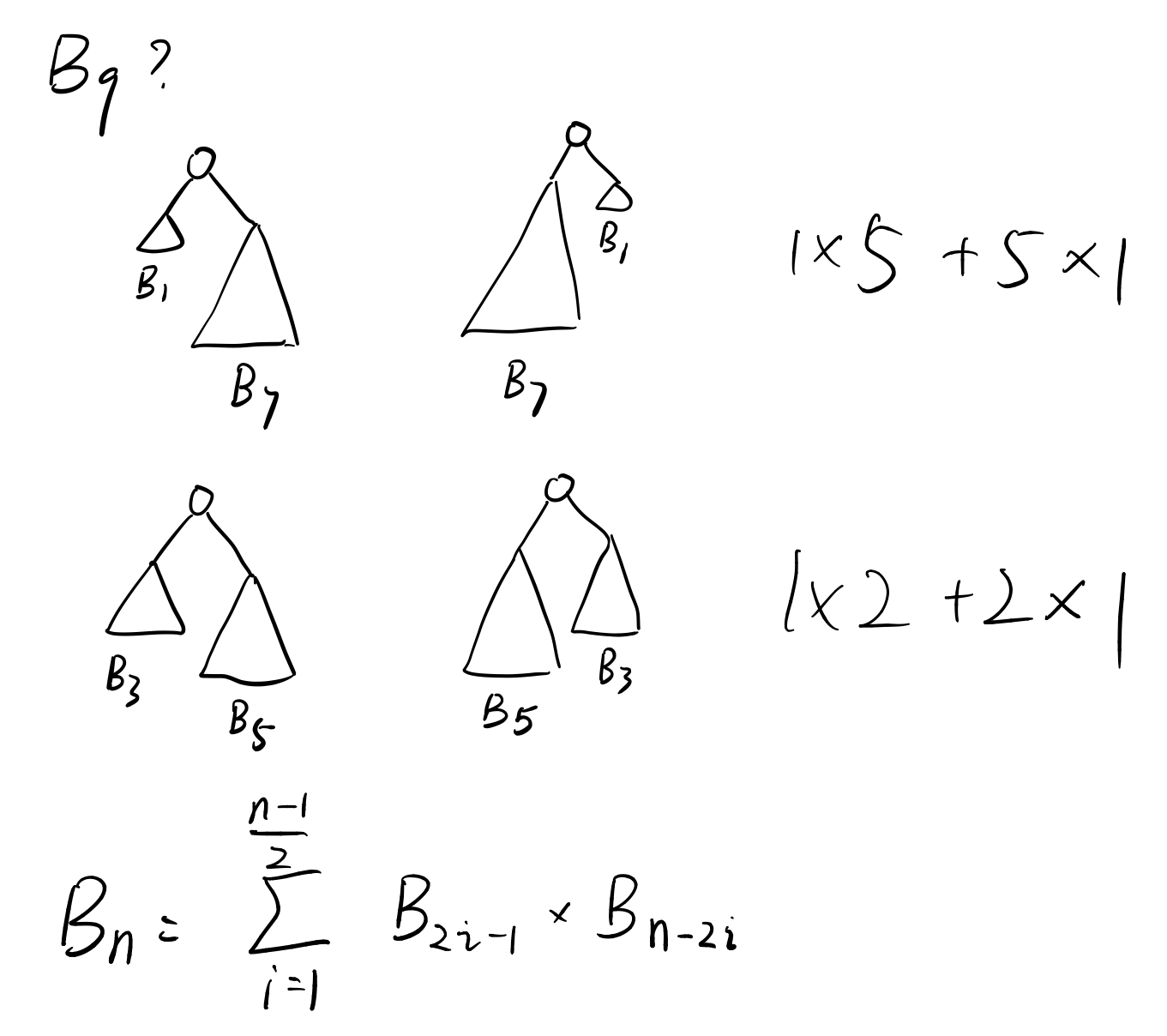
那麼，就可以運用一下數學歸納法。如果能從B_n-2，B_n-4之類的入手，得到一個放縮的式子大於等於2ⁿ的話，那就再好不過了。

不過很可惜，如果直接B_n = 2B_n-2 x B₁ + 2B_n-4 x B₃

但是我們可以驗證（猜想），當n足夠大時，B_(n-1)/2是足夠大於2ⁿ的。那麼只要我們從折半的地方入手，很容易就能從類似B_(n-1)/2 x B_(n-1)/2這樣的式子中推出放縮式。具體細節就不再贅述了，讀者可以自行驗證。

2. 當前有一個大小為n的無序列表，以及一個數S。設計一個O(nlgn)演算法，尋找列表裡面是否有兩個數加和等於S。

既然是nlgn演算法，當然需要先排序一下，這裡的代價就是nlgn了。

然後，可以考慮這樣一個線性的演算法：

假設有序列表為x。現在讓兩個指標，left和right，分別指向x[0]和x[n-1]。

然後，若x[left] + x[right] > S，則right -= 1，而若是 < S，則left += 1。

終止條件為x[left] + x[right] == S或者left == right。

顯然這是一個線性演算法。程式碼如下：

#...處理x，已知S
left = 0
right = n-1
while left < right:
    if x[left] + x[right] < S:
        left 
 
+= 1
    else if x[left] + x[right] > S:
        right -= 1
    else:
        return true
return false

舉一個例子可能有助於理解：

演算法的正確性可以這麼考慮：由於陣列有序，當left右移，l + r的大小就會增加，反之，right左移，l + r就會減小。無論l + r與S有什麼關係，每一次迴圈總能找到進行一次退出或將right - left減少1的操作。由於right - left最大為n -1，因此這個演算法是線性的。

3. 現在有n個處於區間[0, m]的整數，要求經過O(n+m)的預處理之後，可以用O(1)的演算法返回位於指定區間[a, b]之間的數的個數。

仔細思考一下會發現，預處理其實就是製作出一個類似於離散型分佈函式的陣列。

設資料陣列為S，分佈陣列為D。首先，我們可以遍歷S，對於一個數i，就使D[k] += 1。然後得出一個類似分佈律的東西。實際上，把數組裡的每個數除以n，就得到了S的分佈律。

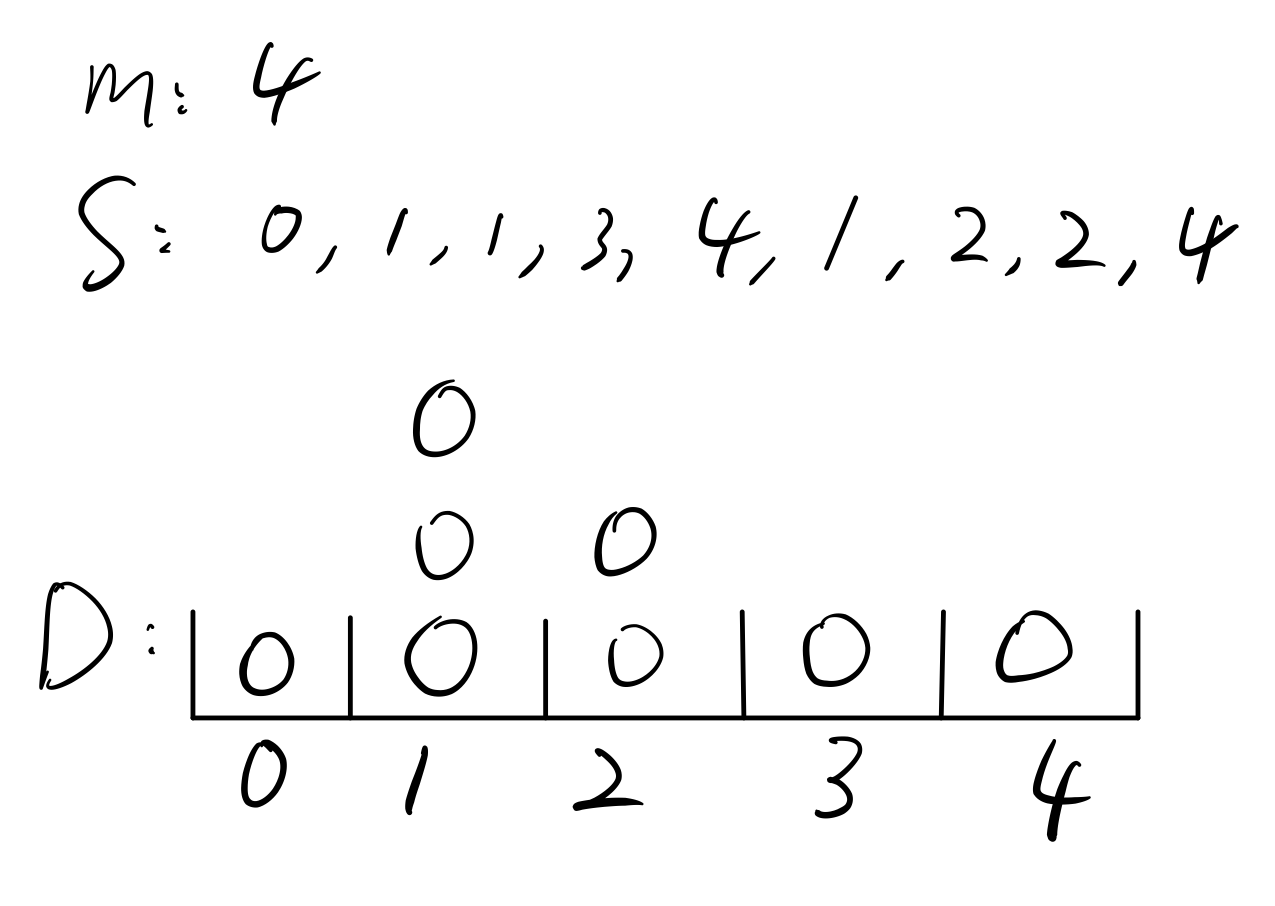
然後，將前一個格的東西加和到後一格，就可以得出分佈函數了。

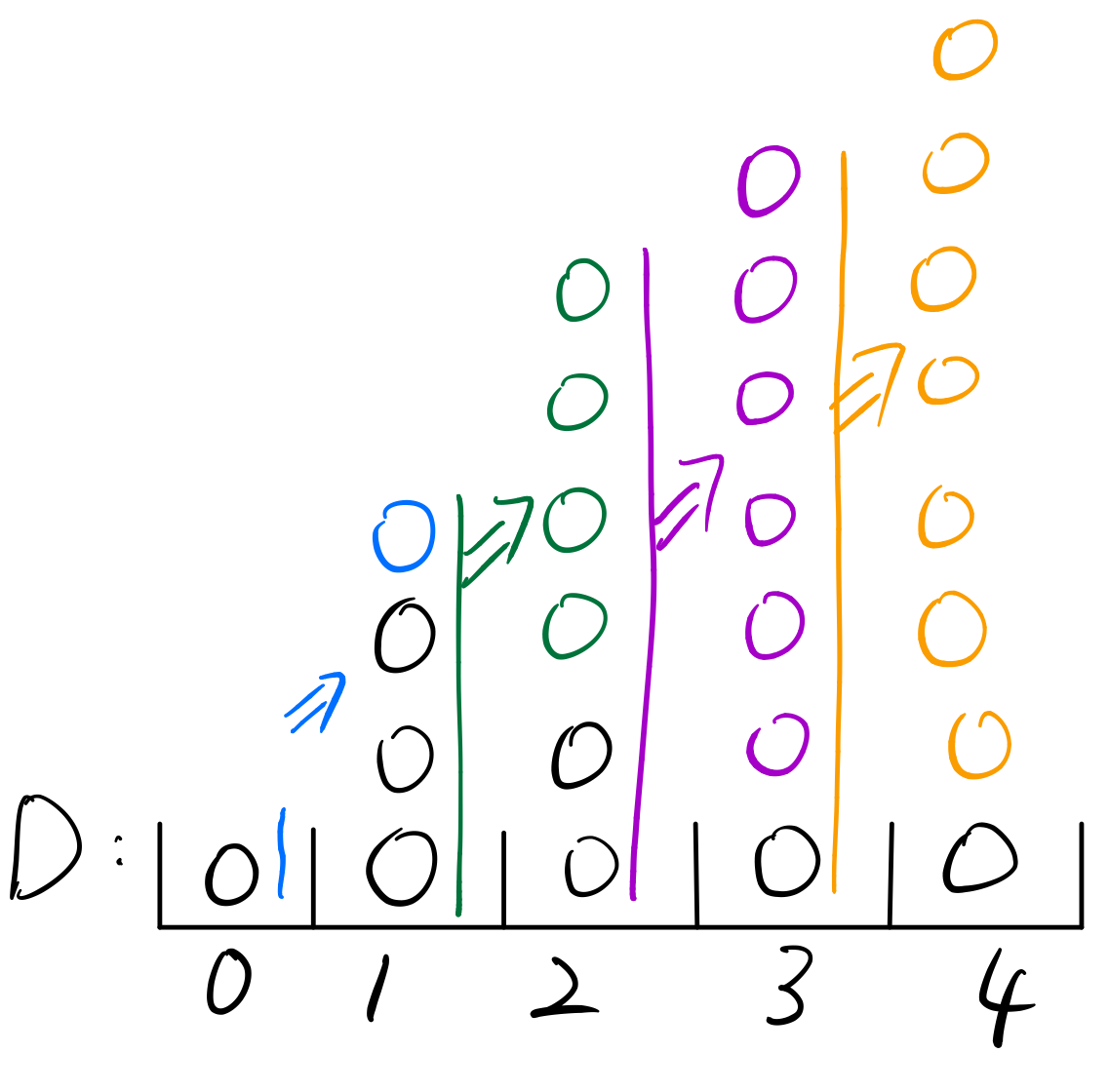
最後要注意，查詢函式是D[b] - D[a - 1]，否則就會缺少a上的數值了！

4. 對於一個棧，給定兩個操作：

Ordered-push( x )：如果x < 棧頂元素first，就彈出first，直到滿足x ≥ first為止，然後插入x。

Pop( x )：彈出first。

用攤還分析計算操作代價。

考慮實際代價：

• O-push：2i + 2。假設彈出了i個元素，則比較次數為i + 1，彈出次數為i，插入次數為1，共2i + 2。
• Pop：1。

那麼，如何分析會計代價呢？

一般的會計代價分析，需要將一個大代價的操作平攤到小代價操作上。然而由於這題的O-push大部分的代價本質上也是pop，所以分攤到小pop操作上顯然是不合適的。

所以，這題需要O-push自我分攤。方案是這樣的：

• 彈出i個元素之前，必然需要先進行i次O-push操作。
• 那麼，就可以將2i分攤到pop出的i個元素中，每個元素分配2的代價。

這樣，會計代價就是：

• O-push：-2i + 2。-2i是分攤出去的，2是被分攤到的。
• Pop：0

所以，攤還代價為：

• O-push：4
• Pop：1

整個資料型別的操作代價是O(1)。

5. 對於一個有向圖，

（1）設計O(n+m)的演算法，判斷從一個特定的點v是否可以到達圖上所有點；

（2）設計O(n+m)的演算法，判斷圖中是否存在點，可達圖上所有點。

先看看第一題。我們可以利用活躍區間，在從v開始進行dfs的時候，如果v是最後一個結束訪問的節點，即可以得出v可以到達所有的點。

除此之外，也可以利用點的著色，看看v之後是否還有白色點。如果沒有則v滿足條件。

我自己記錄了dfs過程中，一個點以自己為根的子樹包含的節點數。如果v的這個數為n，說明v滿足條件。

方法是多種多樣的。

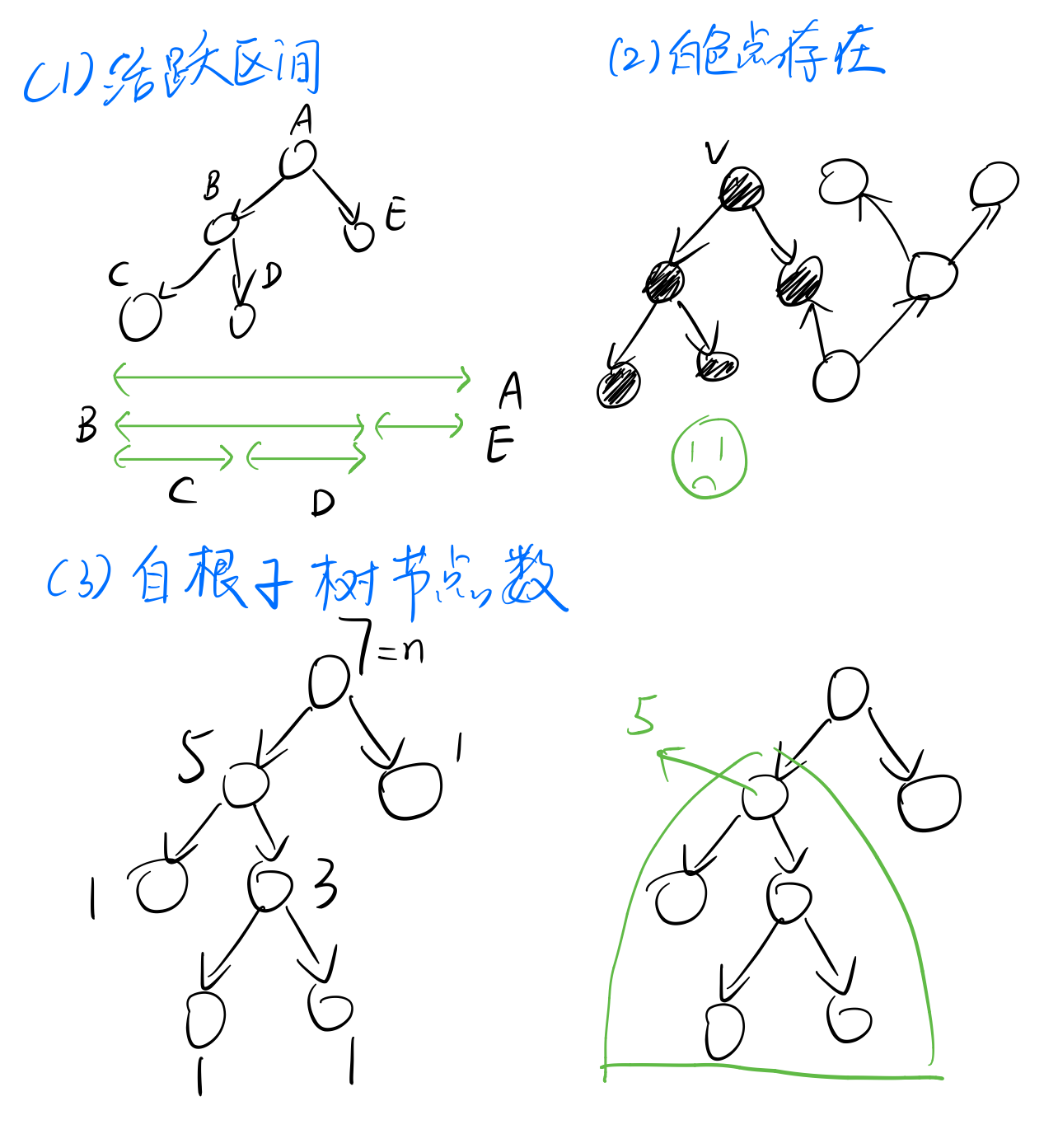
而對於第二題，關鍵在於，在dfs結束後，最後一個dfs樹的根是否可達所有的點。至於為什麼可以仔細想想，大概可以往反證法的方向考慮。

所以基於這個思想，可以在dfs過程中記錄這個最後的根，並在dfs結束後對這個根運用（1）的演算法。

仔細考慮會發現，如果這樣的點存在，那麼如果在dfs過程中，在尋找到根時把根接入，那麼最終只會剩下一個dfs樹。

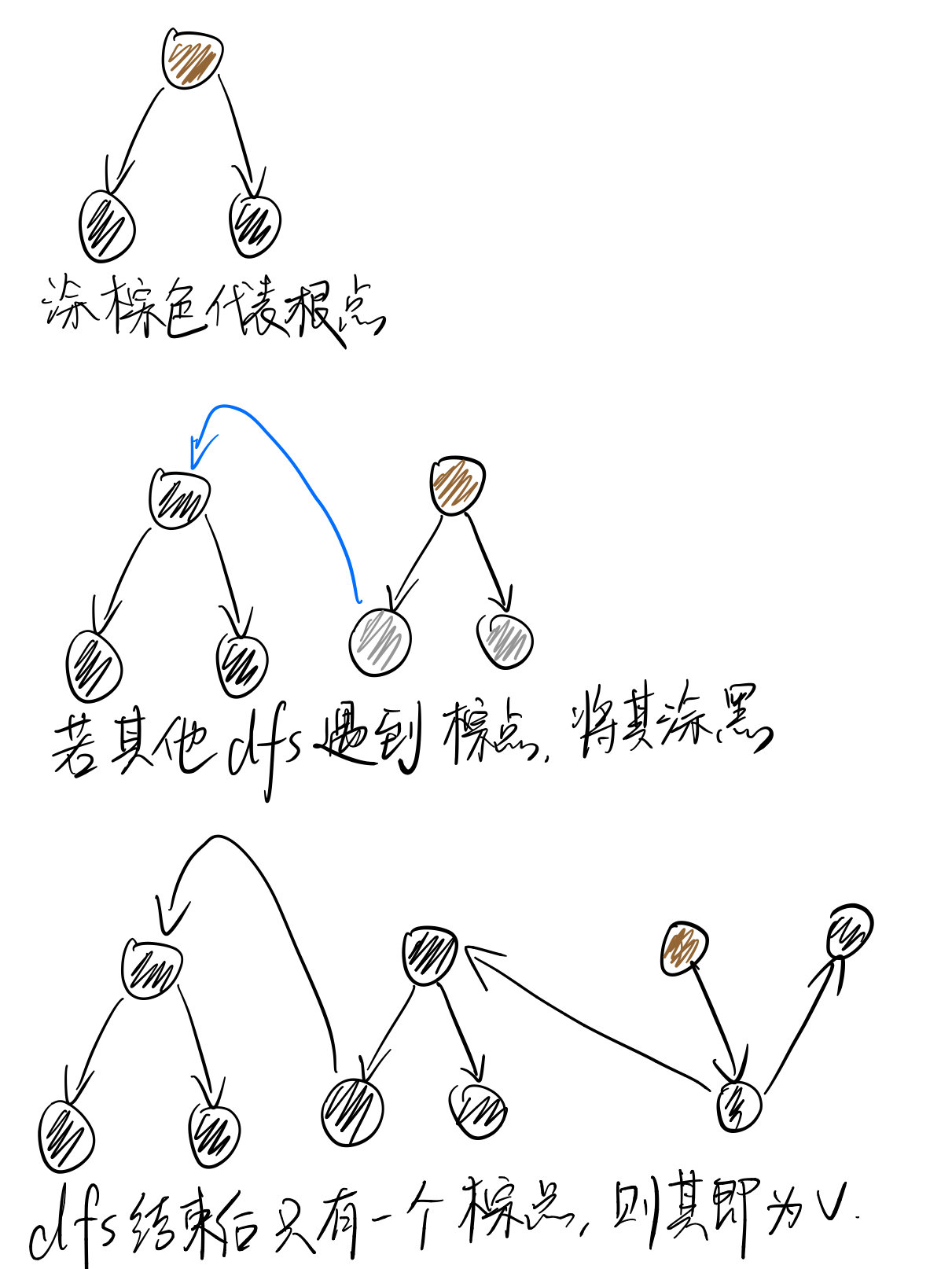
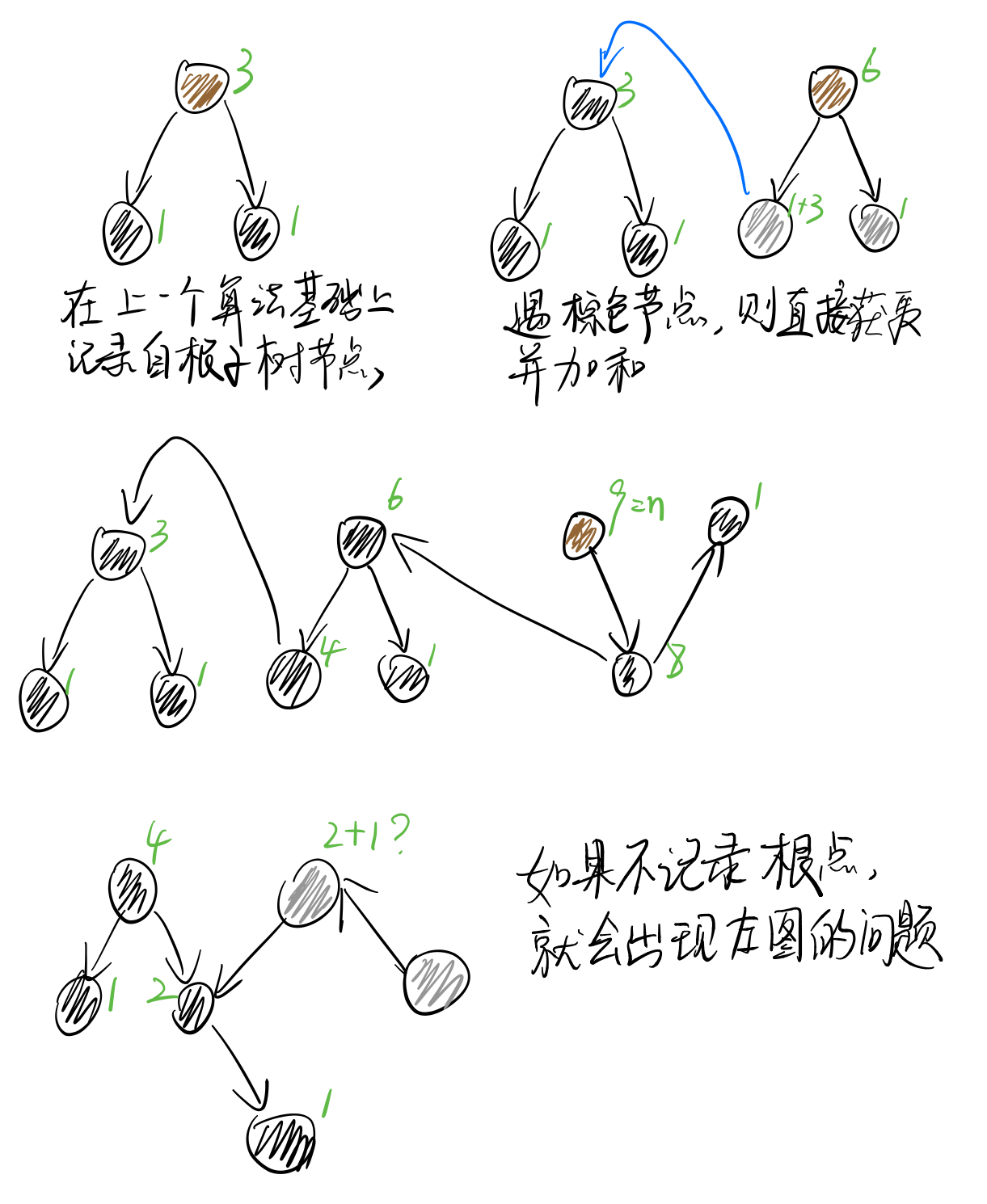
這個時候既可以用記錄自根子樹節點數的方法，也可以用單純記錄根的方法。殊途同歸。

然而要注意，用自根子樹節點數方法時，其實也需要記錄根，而不能僅僅靠黑色節點。否則會出現問題。

6. 待續