https://leetcode.com/problems/3sum/

3Sum實際上是對2sum的封裝。這道題目裡會有重複的數，所以2sum使用夾逼的方法求解。演算法的時間複雜度是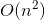，空間複雜度是O(n)。以下分別為C++和Python實現。

struct Solution {
	vector<vector<int>> threeSum(vector<int>& num)
	{
		vector<vector<int>> res;
		if (num.empty() || num.size() <= 2)
			return res;

		std::sort(num.begin(), num.end());
		for (int i = (int)num.size() - 1; i >= 2; i--) {
			if (i<num.size() - 1 && num[i] == num[i + 1])
				continue;

			vector<vector<int>> curRes = twoSum(num, i - 1, -num[i]);
			for (int j = 0; j<curRes.size(); j++)
				curRes[j].push_back(num[i]);

			res.insert(res.begin(), curRes.begin(), curRes.end());
		}

		return res;
	}

	vector<vector<int>> twoSum(vector<int>& num, int end, int target)
	{
		vector<vector<int>> res;
		if (num.empty() || num.size() <= 1)
			return res;

		int l = 0;
		int r = end;
		while (l<r) {
			if (num[l] + num[r] == target) {
				vector<int> item;
				item.push_back(num[l]);
				item.push_back(num[r]);
				res.push_back(item);
				l++;
				r--;
				while (l<r&&num[l] == num[l - 1])
					l++;
				while (l<r&&num[r] == num[r + 1])
					r--;
			}
			else if (num[l] + num[r]>target)
				r--;
			else
				l++;
		}

		return res;
	}
};
 

class Solution:
	def threeSum(self, nums):
		if nums == None or len(nums) < 3:
			return []

		nums.sort()

		res = []
		for i in range(len(nums)-1,0,-1):
			if i < 2:
				break

			if i < (len(nums) - 1) and nums[i] == nums[i+1]:
				continue

			twoSumRes = self.twoSum(nums, i-1, -nums[i])

			for v in twoSumRes:
				v.append(nums[i])
				res.append(v)

		return res

	def twoSum(self, nums, end, target):
		if nums == None or len(nums) < 2:
			return []

		res = []
		l = 0
		r = end
		while l < r :
			if (nums[l] + nums[r]) == target:
				item = []
				item.append(nums[l])
				item.append(nums[r])
				res.append(item)

				l = l + 1
				r = r - 1
				while l < r and nums[l] == nums[l - 1]:
					l = l + 1
				while l < r and nums[r] == nums[r + 1]:
					r = r - 1
			elif (nums[l] + nums[r]) > target:
				r = r - 1
			else:
				l = l + 1

		return res