輸入：輸入資料x1..xm（這些資料是準備進入啟用函式的資料）
計算過程中可以看到,
1.求資料均值；
2.求資料方差；
3.資料進行標準化（個人認為稱作正態化也可以）
4.訓練引數γ，β
5.輸出y通過γ與β的線性變換得到新的值
在正向傳播的時候，通過可學習的γ與β引數求出新的分佈值

在反向傳播的時候，通過鏈式求導方式，求出γ與β以及相關權值
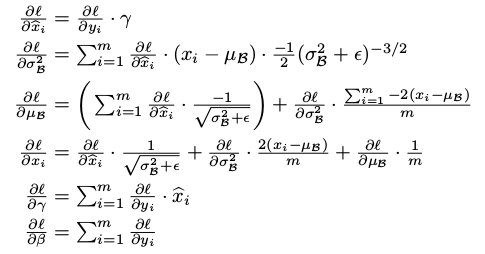3-BN的意義

解決的問題是梯度消失與梯度爆炸。
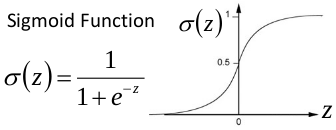
關於梯度消失，以sigmoid函式為例子，sigmoid函式使得輸出在[0,1]之間。

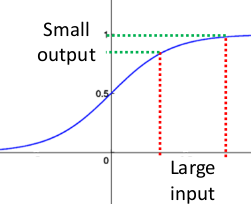
事實上x到了一定大小，經過sigmoid函式的輸出範圍就很小了，參考下圖

如果輸入很大，其對應的斜率就很小，我們知道，其斜率（梯度）在反向傳播中是權值學習速率。所以就會出現如下的問題，

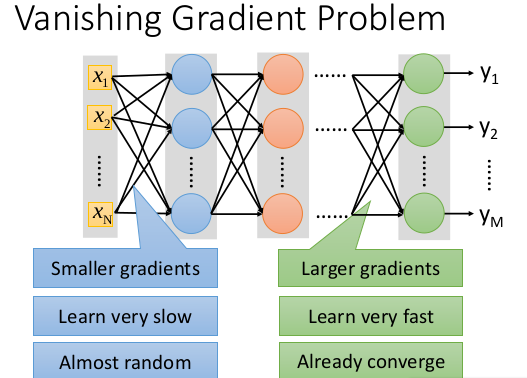
在深度網路中，如果網路的啟用輸出很大，其梯度就很小，學習速率就很慢。假設每層學習梯度都小於最大值0.25，網路有n層，因為鏈式求導的原因，第一層的梯度小於0.25的n次方，所以學習速率就慢，對於最後一層只需對自身求導1次，梯度就大，學習速率就快。
這會造成的影響是在一個很大的深度網路中，淺層基本不學習，權值變化小，後面幾層一直在學習，結果就是，後面幾層基本可以表示整個網路，失去了深度的意義。

關於梯度爆炸，根據鏈式求導法，
第一層偏移量的梯度=啟用層斜率1x權值1x啟用層斜率2x…啟用層斜率(n-1)x權值(n-1)x啟用層斜率n
假如啟用層斜率均為最大值0.25，所有層的權值為100，這樣梯度就會指數增加。4-BN在CNN中的用法

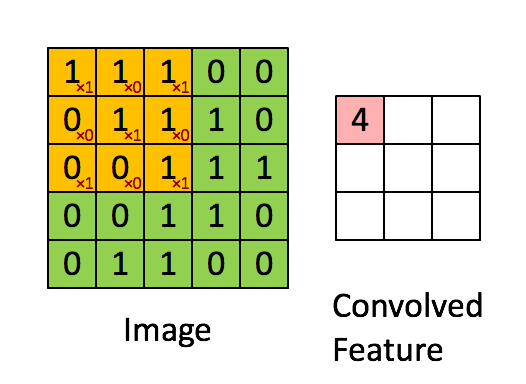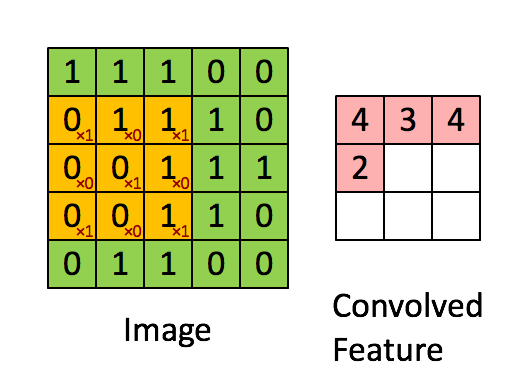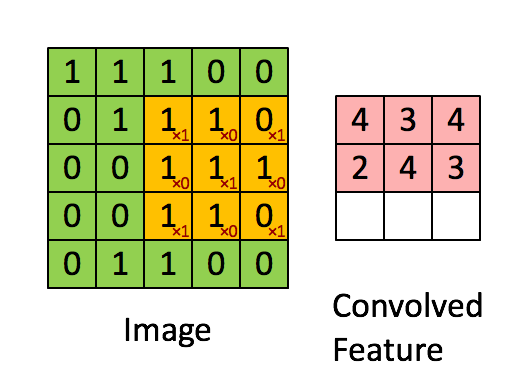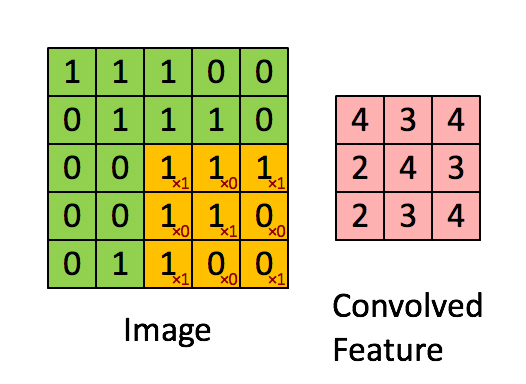
先解釋一下對於圖片卷積是如何使用BN層。

這是文章卷積神經網路CNN（1）中5x5的圖片通過valid卷積得到的3x3特徵圖（粉紅色）。特徵圖裡的值，作為BN的輸入，也就是這9個數值通過BN計算並儲存γ與β，通過γ與β使得輸出與輸入不變。假設輸入的batch_size為m，那就有m*9個數值，計算這m*9個數據的γ與β並儲存。正向傳播過程如上述，對於反向傳播就是根據求得的γ與β計算梯度。
這裡需要著重說明2個細節：
1.網路訓練中以batch_size為最小單位不斷迭代，很顯然，新的batch_size進入網路，機會有新的γ與β，因此，在BN層中，有總圖片數/batch_size組γ與β被儲存下來。
2.影象卷積的過程中，通常是使用多個卷積核，得到多張特徵圖，對於多個的卷積核需要儲存多個的γ與β。

結合論文中給出的使用過程進行解釋

輸入：待進入啟用函式的變數
輸出：
1.對於K維的輸入，假設每一維包含m個變數，所以需要K個迴圈。每個迴圈中按照上面所介紹的方法計算γ與β。這裡的K維，在卷積網路中可以看作是卷積核個數，如網路中第n層有64個卷積核，就需要計算64次。
需要注意，在正向傳播時，會使用γ與β使得BN層輸出與輸入一樣。
2.在反向傳播時利用γ與β求得梯度從而改變訓練權值（變數）。
3.通過不斷迭代直到訓練結束，求得關於不同層的γ與β。如網路有n個BN層，每層根據batch_size決定有多少個變數，設定為m，這裡的mini-batcherB指的是特徵圖大小*batch_size，即m=特徵圖大小*batch_size，因此，對於batch_size為1，這裡的m就是每層特徵圖的大小。
4.不斷遍歷訓練集中的圖片，取出每個batch_size中的γ與β，最後統計每層BN的γ與β各自的和除以圖片數量得到平均直，並對其做無偏估計直作為每一層的E[x]與Var[x]。
5.在預測的正向傳播時，對測試資料求取γ與β，並使用該層的E[x]與Var[x]，通過圖中11:所表示的公式計算BN層輸出。
注意，在預測時，BN層的輸出已經被改變，所以BN層在預測的作用體現在此處5-BN before or after Activation