TSP問題(貪心)
阿新 • • 發佈:2018-12-23
轉自:傳送門
TSP問題(Traveling Salesman Problem,旅行商問題),由威廉哈密頓爵士和英國數學家剋剋曼T.P.Kirkman於19世紀初提出。問題描述如下:
有若干個城市,任何兩個城市之間的距離都是確定的,現要求一旅行商從某城市出發必須經過每一個城市且只在一個城市逗留一次,最後回到出發的城市,問如何事先確定一條最短的線路已保證其旅行的費用最少?
另一個類似的問題為:一個郵遞員從郵局出發,到所轄街道投郵件,最後返回郵局,如果他必須走遍所轄的每條街道至少一次,那麼他應該如何選擇投遞路線,使所走的路程最短?這個描述之所以稱為中國郵遞員問題(Chinese Postman Problem CPP)
為簡化該問題,假設只有A、B、C、D四個城市,各城市的關係如圖所示,權值表示兩個城市之間的的距離。 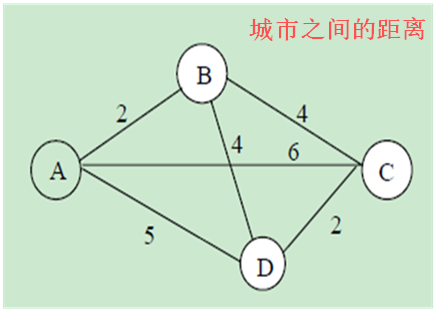
為了將圖中關係資料化,可用如下規則來描述:
城市對映為編號:A——0,B——1,C——2,D——3;
城市之間的距離用二維陣列來表示,記為D[i][j],如:D[0][1]表示城市A與城市B之間的距離,於是D[0][1]=2;
用一維陣列S[i]來儲存訪問過的路徑。
該問題的基本解法為遞迴遍歷,但是會產生組合爆炸問題(時間複雜度為n!),此處不做介紹,而引入一種更為高效的解法:貪心演算法。該演算法描述如下:
貪心演算法:又稱貪婪演算法(greedy algorithm),該演算法是指:在對問題求解時,總是做出當前情況下的最好選擇,否則將來可能會後悔,故名“貪心”。這是一種演算法策略,每次選擇得到的都是區域性最優解
。選擇的策略必須具備無後效性,即某個狀態以前的過程不會影響以後的狀態,只與當前狀態有關。
針對TSP問題,使用貪心演算法的求解的過程為:
1.從某一個城市開始,每次選擇一個城市,直到所有的城市被走完。
2.每次在選擇下一個城市的時候,只考慮當前情況,保證迄今為止經過的路徑總距離最小。
使用貪心演算法求解TSP問題的步驟描述如圖所示:
#include<iostream> #include<cstring> #include<algorithm> #include<vector> #include<cstdio> #include<cmath> #include<string> #define LL long long #define n 4 using namespace std; int main(){ int i,k,j,l; int s[n]; //用於儲存已訪問過的城市 int D[n][n]; //用於記錄兩個城市之間的距離 int sum=0; //用於計算已訪問過的城市的最小路徑長度 int Dtemp;//保證Dtemp比任意任意兩個城市之間的距離都大 int flag;//最為訪問的標誌,若被訪問過則為1,從未被訪問過則為0 i=1;//i是至今已經訪問過的城市 s[0]=0; D[0][1]=2;D[0][2]=6;D[0][3]=5;D[1][0]=2; D[1][2]=4;D[1][3]=4;D[2][0]=6;D[2][1]=4; D[2][3]=2;D[3][0]=5;D[3][1]=4;D[3][2]=2; do{ k=1; //第幾個位置 Dtemp=10000; do{ l=0;flag=0; do{ if(s[l]==k){ //判斷該城市是否被訪問過, flag=1; break; } else{ l++; } }while(l<i); if(flag==0&&D[k][s[i-1]]<Dtemp){ j=k; //j用來 儲存已經訪問過的城市 Dtemp=D[k][s[i-1]]; } k++; }while(k<n); s[i]=j; //將已訪問過的城市儲存起來 i++; sum+=Dtemp; //求出各城市之間的最短距離 }while(i<n); sum+=D[0][j];//D[0][j]為旅行商所在的最後一個城市 for(j=0;j<n;j++){ cout<<s[j]<<" "; } cout<<"\n"<<sum; }



