D. MADMAXtime limit per test1 secondmemory limit per test256 megabytesinputstandard inputoutputstandard output

As we all know, Max is the best video game player among her friends. Her friends were so jealous of hers, that they created an actual game just to prove that she's not the best at games. The game is played on a directed acyclic graph (a DAG) with n vertices and m edges. There's a character written on each edge, a lowercase English letter.

Max and Lucas are playing the game. Max goes first, then Lucas, then Max again and so on. Each player has a marble, initially located at some vertex. Each player in his/her turn should move his/her marble along some edge (a player can move the marble from vertex v to vertex u if there's an outgoing edge from v

 to u). If the player moves his/her marble from vertex v to vertex u, the "character" of that round is the character written on the edge from v to u. There's one additional rule; the ASCII code of character of round i should be greater than or equal to the ASCII code of character of round i - 1 (for i

 > 1). The rounds are numbered for both players together, i. e. Max goes in odd numbers, Lucas goes in even numbers. The player that can't make a move loses the game. The marbles may be at the same vertex at the same time.

Since the game could take a while and Lucas and Max have to focus on finding Dart, they don't have time to play. So they asked you, if they both play optimally, who wins the game?

You have to determine the winner of the game for all initial positions of the marbles.

Input

The first line of input contains two integers n and m (2 ≤ n ≤ 100, ).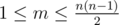

The next m lines contain the edges. Each line contains two integers v, u and a lowercase English letter c, meaning there's an edge from vto u written c on it (1 ≤ v, u ≤ n, v ≠ u). There's at most one edge between any pair of vertices. It is guaranteed that the graph is acyclic.

Output

Print n lines, a string of length n in each one. The j-th character in i-th line should be 'A' if Max will win the game in case her marble is initially at vertex i and Lucas's marble is initially at vertex j, and 'B' otherwise.

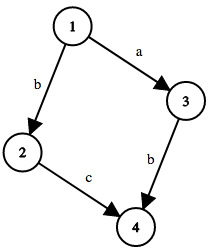
ExamplesinputCopy

4 4
1 2 b
1 3 a
2 4 c
3 4 b

output

BAAA
ABAA
BBBA
BBBB

inputCopy

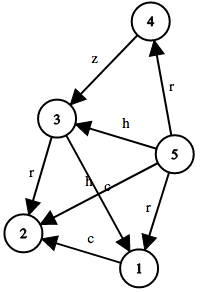
5 8
5 3 h
1 2 c
3 1 c
3 2 r
5 1 r
4 3 z
5 4 r
5 2 h

output

BABBB
BBBBB
AABBB
AAABA
AAAAB

Note

Here's the graph in the first sample test case:

Here's the graph in the second sample test case:

題意：給定一個有向無環圖（DAG），邊權為小寫字母ASCLL值，兩個人A和B分別在兩點出發，一人走一步，每一步算是一輪，這一輪走的邊權一定大於等於上一輪走的邊權，也就是當前人走的邊權一定大於等於另外一個人（上一輪）走過的邊權，誰先沒有路可走就算輸。輸出一個n*n的矩陣，表示當前位置那個人贏了；

思路：博弈的思想，有固定起點的DAG模型，只不過這裡要照顧兩個起點

設dp[f][i][j] f為上一輪對手走過的邊權，i為當前人所在位置，j為對手所在位置，該當前人走，根據博弈論，等於0時，表示當前人先手i 無路可走；dp[f][i][j]的下一步為dp[f1][j][k],f1大於f，現在先手變成了j，k為i的下一步

若存在一個 dp[f1][j][k] == 0，就說明dp[f][i][j] 有可能贏，按照博弈論上的必敗態、必勝態說，這時候dp[f][i][j]為必勝態；

若所有的 dp[f1][j][k] == 1, 就說明dp[f][i][j]為必敗態；

這裡也用到了記憶化搜尋；

程式碼：

#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
#include<vector>
#define Max 110
int	dp[30][Max][Max];
int n,m;

struct node 
{
	int to,vec;
};
vector<node> v[Max];
void init()
{
	int i,j;
	for(i = 0; i <= n; i ++)
		v[i].clear();
	memset(dp,-1,sizeof(dp));
}

int dfs(int f,int x,int y)
{
	if(dp[f][x][y] != -1) return dp[f][x][y];
	for(int i = 0;i< v[x].size();i ++)
	{
		node tt = v[x][i];
		if(tt.vec >= f&&dfs(tt.vec,y,tt.to) == 0)
			return dp[f][x][y] = 1;
	}
	return dp[f][x][y] = 0;
}
int main()
{
	int i,j;
	while(~scanf("%d%d",&n,&m))
	{
		int x,y;
		char c;
		init();
		while(m--)
		{
			scanf("%d %d %c",&x,&y,&c);
			node tt;
			tt.to = y;
			tt.vec = c - 'a' + 1;
			v[x].push_back(tt);
		}
		for(i = 1; i <= n; i ++)
		{
			for(j = 1; j <= n; j ++)
			{
				if(dfs(0,i,j) == 1) printf("A");
				else printf("B"); 	
			}
			printf("\n");
		}
	}
	return 0;	
}