time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Vasya owns a cornfield which can be defined with two integers nn and dd. The cornfield can be represented as rectangle with vertices having Cartesian coordinates (0,d),(d,0),(n,n−d)(0,d),(d,0),(n,n−d) and (n−d,n)(n−d,n).

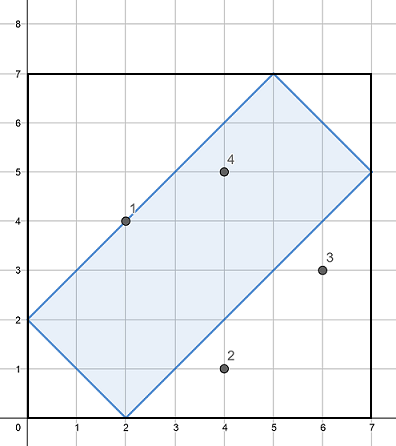An example of a cornfield with n=7n=7 and d=2d=2.

Vasya also knows that there are mm grasshoppers near the field (maybe even inside it). The ii-th grasshopper is at the point (xi,yi)(xi,yi). Vasya does not like when grasshoppers eat his corn, so for each grasshopper he wants to know whether its position is inside the cornfield (including the border) or outside.

Help Vasya! For each grasshopper determine if it is inside the field (including the border).

Input

The first line contains two integers nn and dd (1≤d<n≤1001≤d<n≤100).

The second line contains a single integer mm (1≤m≤1001≤m≤100) — the number of grasshoppers.

The ii-th of the next mm lines contains two integers xixi and yiyi (0≤xi,yi≤n0≤xi,yi≤n) — position of the ii-th grasshopper.

Output

Print mm lines. The ii-th line should contain "YES" if the position of the ii-th grasshopper lies inside or on the border of the cornfield. Otherwise the ii-th line should contain "NO".

You can print each letter in any case (upper or lower).

Examples

input

Copy

7 2
4
2 4
4 1
6 3
4 5

output

Copy

YES
NO
NO
YES

input

Copy

8 7
4
4 4
2 8
8 1
6 1

output

Copy

YES
NO
YES
YES

Note

The cornfield from the first example is pictured above. Grasshoppers with indices 11 (coordinates (2,4)(2,4)) and 44 (coordinates (4,5)(4,5)) are inside the cornfield.

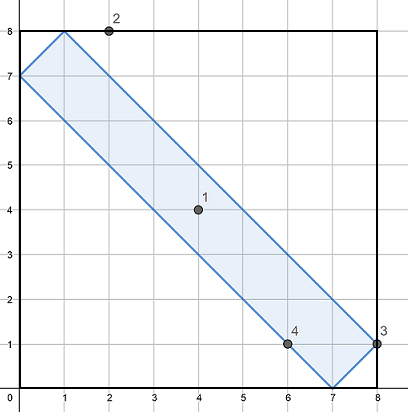
The cornfield from the second example is pictured below. Grasshoppers with indices 11 (coordinates (4,4)(4,4)), 33 (coordinates (8,1)(8,1)) and 44(coordinates (6,1)(6,1)) are inside the cornfield.

很好的一個解析幾何題目！

題目大意：給定一個n * nn∗n的範圍以及一個數字dd，再給定mm個點，要你求這mm個點是否分別在 (0,d),(d,0),(n,n - d)(n - d,n)(0,d),(d,0),(n,n−d)(n−d,n) 圍成的範圍裡。

解析：真的是一道好題！

我們考慮先求出這四條直線的解析式。首先是過 (0,d),(d,0)(0,d),(d,0) 的：k = \frac{d - 0}{0 - d} = -1k=0−dd−0​=−1，b = db=d。於是乎 y= - x+dy=−x+d 推出 x + y = dx+y=d。

過 (0,d),(n - d,n)(0,d),(n−d,n) 的：k = \frac{d - n}{0 - (n - d)} = 1k=0−(n−d)d−n​=1，b = db=d，於是乎 y = x + dy=x+d 推出 x - y = -dx−y=−d。

過(n - d,n), (n, n - d)(n−d,n),(n,n−d)的：k = \frac{n - (n - d)}{(n - d) - n} = -1k=(n−d)−nn−(n−d)​=−1，b = -2n + db=−2n+d，於是乎 y = - x - 2n + dy=−x−2n+d 推出 x - y = 2n - dx−y=2n−d。

過(d,0), (n, n - d)(d,0),(n,n−d)的：k = \frac{0 - (n - d)}{d - n} = 1k=d−n0−(n−d)​=1，b = -db=−d，於是乎 y = x - dy=x−d 推出 x - y = dx−y=d。

此時我們再考慮如何判斷這些點是否在裡面即可。

於是乎問題轉化成一個線性規劃問題。

即：給定 44 條直線，求給定的點是否是在這四個點圍成的矩形中。

於是只要滿足：

d \leq x + yd≤x+yx + y \leq 2n - dx+y≤2n−d-d \leq x - y−d≤x−yx - y \leq dx−y≤d

即可。

#include<stdio.h>
#include<iostream>
using namespace std;
int main()
{int n,d;
cin>>n>>d;
int m;
cin>>m;
for(int i=1;i<=m;i++)
{
    int x,y;
    cin>>x>>y;
    if((x+y>=d)&&(x+y<=2*n-d)&&(-d<=x-y)&&(x-y<=d))
        cout<<"YES"<<endl;
    else cout<<"NO"<<endl;
}
	return 0;
}