B-樹詳細分析及B樹B-樹B+樹B*樹概念
B- 樹是為了磁碟或其它儲存裝置而設計的一種多叉(下面你會看到,相對於二叉,B樹每個內結點有多個分支,即多叉)平衡查詢樹。
B- 樹又叫平衡多路查詢樹。一棵m階的B 樹 (m叉樹)的特性如下:
- 樹中每個結點最多含有m個孩子(m>=2);
- 除根結點和葉子結點外,其它每個結點至少有[ceil(m / 2)]個孩子(其中ceil(x)是一個取上限的函式);
- 若根結點不是葉子結點,則至少有2個孩子(特殊情況:沒有孩子的根結點,即根結點為葉子結點,整棵樹只有一個根節點);
- 所有葉子結點都出現在同一層,葉子結點不包含任何關鍵字資訊(可以看做是外部接點或查詢失敗的接點,實際上這些結點不存在,指向這些結點的指標都為null);
- 每個非終端結點中包含有n個關鍵字資訊: (n,P0,K1,P1,K2,P2,......,Kn,Pn)。其中:
a) Ki (i=1...n)為關鍵字,且關鍵字按順序升序排序K(i-1)< Ki。
b) Pi為指向子樹根的接點,且指標P(i-1)指向子樹種所有結點的關鍵字均小於Ki,但都大於K(i-1)。
c) 關鍵字的個數n必須滿足: [ceil(m / 2)-1]<= n <= m-1。
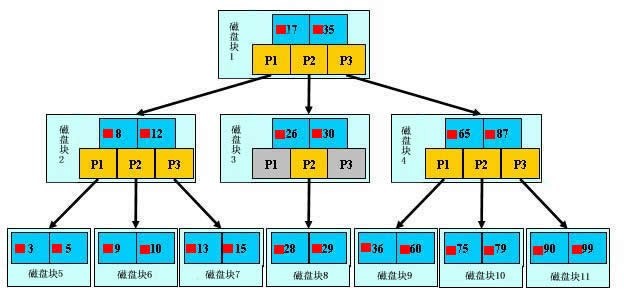
來模擬下查詢檔案29的過程:
(1) 根據根結點指標找到檔案目錄的根磁碟塊1,將其中的資訊匯入記憶體。【磁碟IO操作1次】
(2) 此時記憶體中有兩個檔名17,35和三個儲存其他磁碟頁面地址的資料。根據演算法我們發現17<29<35,因此我們找到指標p2。
(3) 根據p2指標,我們定位到磁碟塊3,並將其中的資訊匯入記憶體。【磁碟IO操作2次】
(4) 此時記憶體中有兩個檔名26,30和三個儲存其他磁碟頁面地址的資料。根據演算法我們發現26<29<30,因此我們找到指標p2。
(5) 根據p2指標,我們定位到磁碟塊8,並將其中的資訊匯入記憶體。【磁碟IO操作3次】
(6) 此時記憶體中有兩個檔名28,29。根據演算法我們查詢到檔案29,並定位了該檔案記憶體的磁碟地址。
插入操作
生成從空樹開始,逐個插入關鍵字。但是由於B_樹節點關鍵字必須大於等於[ceil(m/2)-1],所以每次插入一個關鍵字不是在樹中新增一個葉子結點,而是首先在最底層的某個非終端節點中新增一個“關鍵字”,該結點的關鍵字不超過m-1,則插入完成;否則要產生結點的“分裂”,將一半數量的關鍵字元素分裂到新的其相鄰右結點中,中間關鍵字元素上移到父結點中。
1、咱們通過一個例項來逐步講解下。插入以下字元字母到一棵空的B 樹中(非根結點關鍵字數小了(小於2個)就合併,大了(超過4個)就分裂):C N G A H E K Q M F W L T Z D P R X Y S,首先,結點空間足夠,4個字母插入相同的結點中,如下圖:
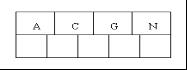
2、當咱們試著插入H時,結點發現空間不夠,以致將其分裂成2個結點,移動中間元素G上移到新的根結點中,在實現過程中,咱們把A和C留在當前結點中,而H和N放置新的其右鄰居結點中。如下圖:
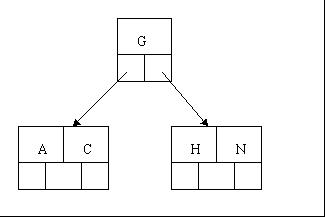
3、當咱們插入E,K,Q時,不需要任何分裂操作
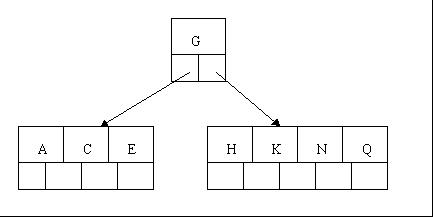
4、插入M需要一次分裂,注意M恰好是中間關鍵字元素,以致向上移到父節點中
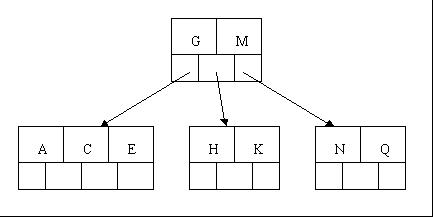
5、插入F,W,L,T不需要任何分裂操作
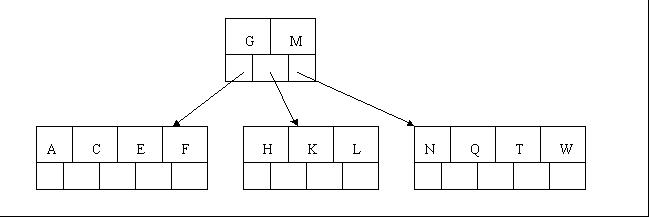
6、插入Z時,最右的葉子結點空間滿了,需要進行分裂操作,中間元素T上移到父節點中,注意通過上移中間元素,樹最終還是保持平衡,分裂結果的結點存在2個關鍵字元素。

7、插入D時,導致最左邊的葉子結點被分裂,D恰好也是中間元素,上移到父節點中,然後字母P,R,X,Y陸續插入不需要任何分裂操作(別忘了,樹中至多5個孩子)。
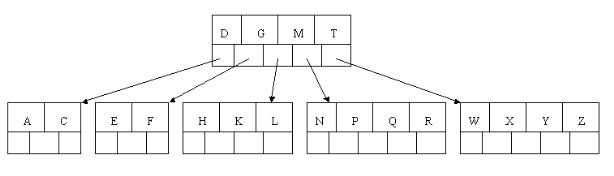
8、最後,當插入S時,含有N,P,Q,R的結點需要分裂,把中間元素Q上移到父節點中,但是情況來了,父節點中空間已經滿了,所以也要進行分裂,將父節點中的中間元素M上移到新形成的根結點中,注意以前在父節點中的第三個指標在修改後包括D和G節點中。這樣具體插入操作的完成。
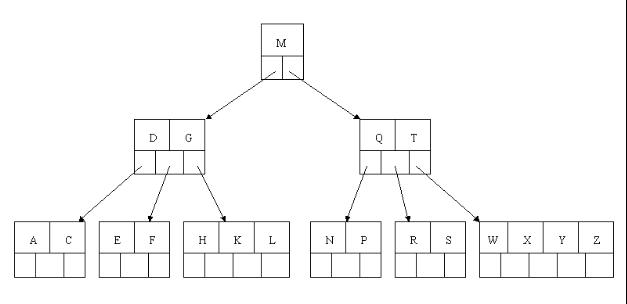
刪除操作
首先查詢B樹中需刪除的元素,如果該元素在B樹中存在,則將該元素在其結點中進行刪除,如果刪除該元素後,首先判斷該元素是否有左右孩子結點,如果有,則上移孩子結點中的某相近元素到父節點中,然後是移動之後的情況;如果沒有,直接刪除後,移動之後的情況。
刪除元素,移動相應元素之後,如果某結點中元素數目(即關鍵字數)小於ceil(m/2)-1,則需要看其某相鄰兄弟結點是否豐滿(結點中元素個數大於ceil(m/2)-1)(還記得第一節中關於B樹的第5個特性中的c點麼?: c)除根結點之外的結點(包括葉子結點)的關鍵字的個數n必須滿足: (ceil(m / 2)-1)<= n <= m-1。m表示最多含有m個孩子,n表示關鍵字數。在本小節中舉的一顆B樹的示例中,關鍵字數n滿足:2<=n<=4),如果豐滿,則向父節點借一個元素來滿足條件;如果其相鄰兄弟都剛脫貧,即借了之後其結點數目小於ceil(m/2)-1,則該結點與其相鄰的某一兄弟結點進行“合併”成一個結點,以此來滿足條件。那咱們通過下面例項來詳細瞭解吧。
以上述插入操作構造的一棵5階B樹(樹中最多含有m(m=5)個孩子,因此關鍵字數最小為ceil(m / 2)-1=2。還是這句話,關鍵字數小了(小於2個)就合併,大了(超過4個)就分裂)為例,依次刪除H,T,R,E。

1、首先刪除元素H,當然首先查詢H,H在一個葉子結點中,且該葉子結點元素數目3大於最小元素數目ceil(m/2)-1=2,則操作很簡單,咱們只需要移動K至原來H的位置,移動L至K的位置(也就是結點中刪除元素後面的元素向前移動)
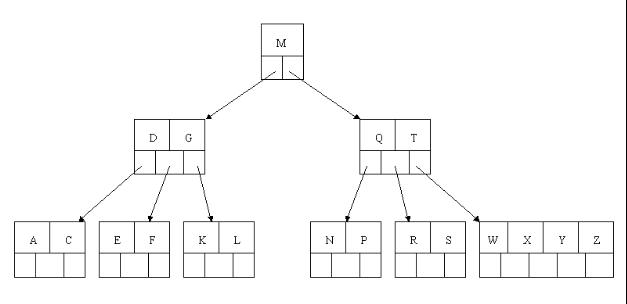
2、下一步,刪除T,因為T沒有在葉子結點中,而是在中間結點中找到,咱們發現他的繼承者W(字母升序的下個元素),將W上移到T的位置,然後將原包含W的孩子結點中的W進行刪除,這裡恰好刪除W後,該孩子結點中元素個數大於2,無需進行合併操作。
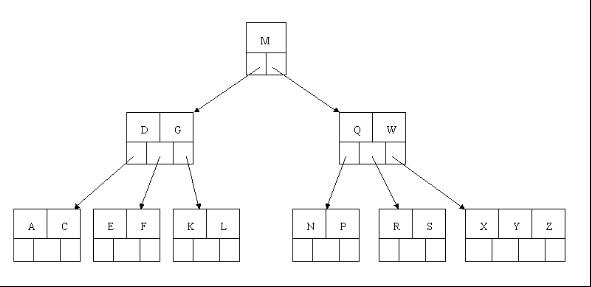
3、下一步刪除R,R在葉子結點中,但是該結點中元素數目為2,刪除導致只有1個元素,已經小於最小元素數目ceil(5/2)-1=2,而由前面我們已經知道:如果其某個相鄰兄弟結點中比較豐滿(元素個數大於ceil(5/2)-1=2),則可以向父結點借一個元素,然後將最豐滿的相鄰兄弟結點中上移最後或最前一個元素到父節點中(有沒有看到紅黑樹中左旋操作的影子?),在這個例項中,右相鄰兄弟結點中比較豐滿(3個元素大於2),所以先向父節點借一個元素W下移到該葉子結點中,代替原來S的位置,S前移;然後X在相鄰右兄弟結點中上移到父結點中,最後在相鄰右兄弟結點中刪除X,後面元素前移。
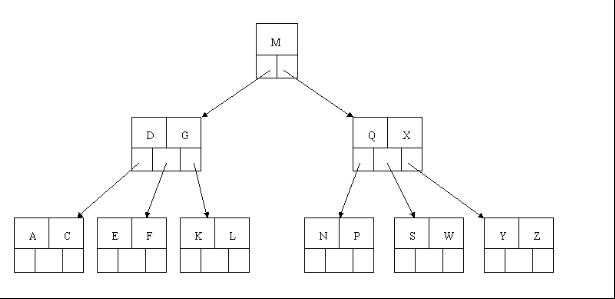
4、最後一步刪除E, 刪除後會導致很多問題,因為E所在的結點數目剛好達標,剛好滿足最小元素個數(ceil(5/2)-1=2),而相鄰的兄弟結點也是同樣的情況,刪除一個元素都不能滿足條件,所以需要該節點與某相鄰兄弟結點進行合併操作;首先移動父結點中的元素(該元素在兩個需要合併的兩個結點元素之間)下移到其子結點中,然後將這兩個結點進行合併成一個結點。所以在該例項中,咱們首先將父節點中的元素D下移到已經刪除E而只有F的結點中,然後將含有D和F的結點和含有A,C的相鄰兄弟結點進行合併成一個結點。
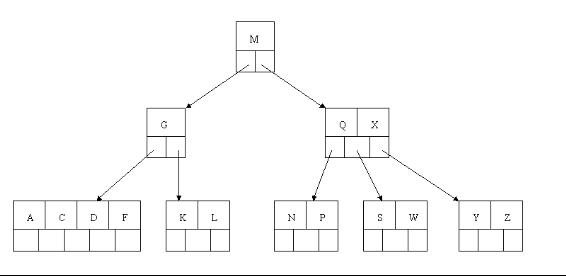
5、也許你認為這樣刪除操作已經結束了,其實不然,在看看上圖,對於這種特殊情況,你立即會發現父節點只包含一個元素G,沒達標(因為非根節點包括葉子結點的關鍵字數n必須滿足於2=<n<=4,而此處的n=1),這是不能夠接受的。如果這個問題結點的相鄰兄弟比較豐滿,則可以向父結點借一個元素。假設這時右兄弟結點(含有Q,X)有一個以上的元素(Q右邊還有元素),然後咱們將M下移到元素很少的子結點中,將Q上移到M的位置,這時,Q的左子樹將變成M的右子樹,也就是含有N,P結點被依附在M的右指標上。所以在這個例項中,咱們沒有辦法去借一個元素,只能與兄弟結點進行合併成一個結點,而根結點中的唯一元素M下移到子結點,這樣,樹的高度減少一層。

為了進一步詳細討論刪除的情況,再舉另外一個例項:
這裡是一棵不同的5序B樹,那咱們試著刪除C
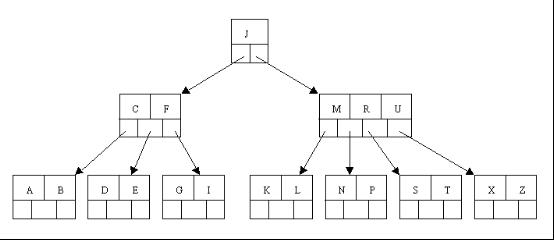
於是將刪除元素C的右子結點中的D元素上移到C的位置,但是出現上移元素後,只有一個元素的結點的情況。
又因為含有E的結點,其相鄰兄弟結點才剛脫貧(最少元素個數為2),不可能向父節點借元素,所以只能進行合併操作,於是這裡將含有A,B的左兄弟結點和含有E的結點進行合併成一個結點。

這樣又出現只含有一個元素F結點的情況,這時,其相鄰的兄弟結點是豐滿的(元素個數為3>最小元素個數2),這樣就可以想父結點借元素了,把父結點中的J下移到該結點中,相應的如果結點中J後有元素則前移,然後相鄰兄弟結點中的第一個元素(或者最後一個元素)上移到父節點中,後面的元素(或者前面的元素)前移(或者後移);注意含有K,L的結點以前依附在M的左邊,現在變為依附在J的右邊。這樣每個結點都滿足B樹結構性質。
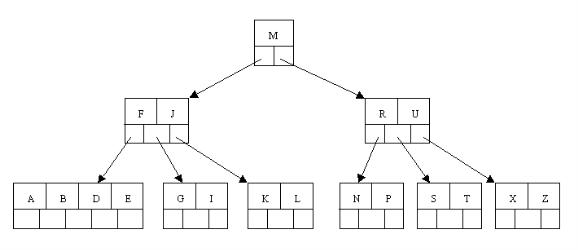
從以上操作可看出:除根結點之外的結點(包括葉子結點)的關鍵字的個數n滿足:(ceil(m / 2)-1)<= n <= m-1,即2<=n<=4。這也佐證了咱們之前的觀點。刪除操作完。
在B_樹中關鍵字分佈在整個B_樹,並且在上層結點中出現過的關鍵字不再出現在最底層的結點中。順序鏈中所有的關鍵字不能連線在一起。
一顆m階的B+樹和m階的B_樹的差異在於:
1.有n棵子樹的結點中含有n個關鍵字; (而B樹是n棵子樹有n-1個關鍵字)
2.所有的葉子結點中包含了全部關鍵字的資訊,及指向含有這些關鍵字記錄的指標,且葉子結點本身依關鍵字的大小自小而大的順序連結。(而B樹的葉子節點並沒有包括全部需要查詢的資訊)
3.所有的非終端結點可以看成是索引部分,結點中僅含有其子樹根結點中最大(或最小)關鍵字。 (而B 樹的非終節點也包含需要查詢的有效資訊)
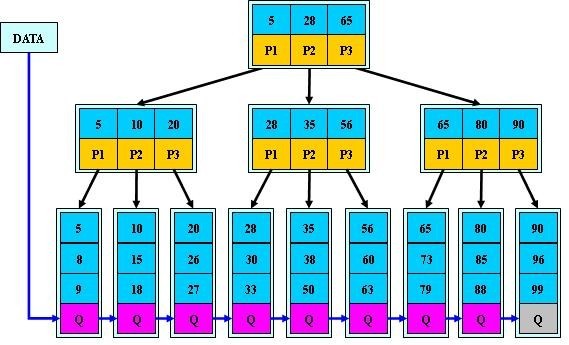
B+樹的主要優點:非終端結點僅僅起高層索引作用,而B樹非終端結點的關鍵字除作子樹分界外,本身還是實際記錄的有效關鍵字(含記錄指標),因此相同的結點空間,B+樹可以設計的階樹比B樹大,相同的索引,B+樹的索引層數比B樹少,因此檢索速度比B樹快。此外,B+樹葉子結點包含完整的索引資訊,可以較方便地表示檔案的稀疏索引。最後,B+樹的檢索、插入和刪除都在葉子結點進行,比B樹相對簡單
B樹B-樹B+樹B*樹概念
B樹
即二叉搜尋樹:
1.所有非葉子結點至多擁有兩個兒子(Left和Right);
2.所有結點儲存一個關鍵字;
3.非葉子結點的左指標指向小於其關鍵字的子樹,右指標指向大於其關鍵字的子樹;
如:

B樹的搜尋,從根結點開始,如果查詢的關鍵字與結點的關鍵字相等,那麼就命中;否則,如果查詢關鍵字比結點關鍵字小,就進入左兒子;如果比結點關鍵字大,就進入右兒子;如果左兒子或右兒子的指標為空,則報告找不到相應的關鍵字;
如果B樹的所有非葉子結點的左右子樹的結點數目均保持差不多(平衡),那麼B樹的搜尋效能逼近二分查詢;但它比連續記憶體空間的二分查詢的優點是,改變B樹結構(插入與刪除結點)不需要移動大段的記憶體資料,甚至通常是常數開銷;
如:

但B樹在經過多次插入與刪除後,有可能導致不同的結構:

右邊也是一個B樹,但它的搜尋效能已經是線性的了;同樣的關鍵字集合有可能導致不同的樹結構索引;所以,使用B樹還要考慮儘可能讓B樹保持左圖的結構,和避免右圖的結構,也就是所謂的“平衡”問題;
實際使用的B樹都是在原B樹的基礎上加上平衡演算法,即“平衡二叉樹”;如何保持B樹結點分佈均勻的平衡演算法是平衡二叉樹的關鍵;平衡演算法是一種在B樹中插入和刪除結點的策略;
B-樹
是一種多路搜尋樹(並不是二叉的):
1.定義任意非葉子結點最多隻有M個兒子;且M>2;
2.根結點的兒子數為[2, M];
3.除根結點以外的非葉子結點的兒子數為[M/2, M];
4.每個結點存放至少M/2-1(取上整)和至多M-1個關鍵字;(至少2個關鍵字)
5.非葉子結點的關鍵字個數=指向兒子的指標個數-1;
6.非葉子結點的關鍵字:K[1], K[2], …, K[M-1];且K[i] < K[i+1];
7.非葉子結點的指標:P[1], P[2], …, P[M];其中P[1]指向關鍵字小於K[1]的子樹,P[M]指向關鍵字大於K[M-1]的子樹,其它P[i]指向關鍵字屬於(K[i-1], K[i])的子樹;
8.所有葉子結點位於同一層;
如:(M=3)

B-樹的搜尋,從根結點開始,對結點內的關鍵字(有序)序列進行二分查詢,如果命中則結束,否則進入查詢關鍵字所屬範圍的兒子結點;重複,直到所對應的兒子指標為空,或已經是葉子結點;
B-樹的特性:
1.關鍵字集合分佈在整顆樹中;
2.任何一個關鍵字出現且只出現在一個結點中;
3.搜尋有可能在非葉子結點結束;
4.其搜尋效能等價於在關鍵字全集內做一次二分查詢;
5.自動層次控制;
由於限制了除根結點以外的非葉子結點,至少含有M/2個兒子,確保了結點的至少利用率,其最底搜尋效能為:
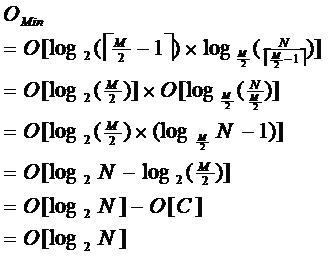
其中,M為設定的非葉子結點最多子樹個數,N為關鍵字總數;
所以B-樹的效能總是等價於二分查詢(與M值無關),也就沒有B樹平衡的問題;
由於M/2的限制,在插入結點時,如果結點已滿,需要將結點分裂為兩個各佔M/2的結點;刪除結點時,需將兩個不足M/2的兄弟結點合併;
B+樹
B+樹是B-樹的變體,也是一種多路搜尋樹:
1.其定義基本與B-樹同,除了:
2.非葉子結點的子樹指標與關鍵字個數相同;
3.非葉子結點的子樹指標P[i],指向關鍵字值屬於[K[i], K[i+1])的子樹(B-樹是開區間);
5.為所有葉子結點增加一個鏈指標;
6.所有關鍵字都在葉子結點出現;
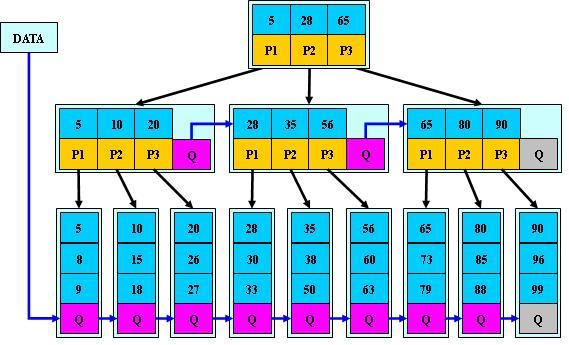
如:(M=3)

B+的搜尋與B-樹也基本相同,區別是B+樹只有達到葉子結點才命中(B-樹可以在非葉子結點命中),其效能也等價於在關鍵字全集做一次二分查詢;
B+的特性:
1.所有關鍵字都出現在葉子結點的連結串列中(稠密索引),且連結串列中的關鍵字恰好是有序的;
2.不可能在非葉子結點命中;
3.非葉子結點相當於是葉子結點的索引(稀疏索引),葉子結點相當於是儲存(關鍵字)資料的資料層;
4.更適合檔案索引系統;
B*樹
是B+樹的變體,在B+樹的非根和非葉子結點再增加指向兄弟的指標;
B*樹定義了非葉子結點關鍵字個數至少為(2/3)*M,即塊的最低使用率為2/3(代替B+樹的1/2);
B+樹的分裂:當一個結點滿時,分配一個新的結點,並將原結點中1/2的資料複製到新結點,最後在父結點中增加新結點的指標;B+樹的分裂隻影響原結點和父結點,而不會影響兄弟結點,所以它不需要指向兄弟的指標;
B*樹的分裂:當一個結點滿時,如果它的下一個兄弟結點未滿,那麼將一部分資料移到兄弟結點中,再在原結點插入關鍵字,最後修改父結點中兄弟結點的關鍵字(因為兄弟結點的關鍵字範圍改變了);如果兄弟也滿了,則在原結點與兄弟結點之間增加新結點,並各複製1/3的資料到新結點,最後在父結點增加新結點的指標;
所以,B*樹分配新結點的概率比B+樹要低,空間使用率更高;
小結
B樹:二叉樹,每個結點只儲存一個關鍵字,等於則命中,小於走左結點,大於走右結點;
B-樹:多路搜尋樹,每個結點儲存M/2到M個關鍵字,非葉子結點儲存指向關鍵字範圍的子結點;
所有關鍵字在整顆樹中出現,且只出現一次,非葉子結點可以命中;
B+樹:在B-樹基礎上,為葉子結點增加連結串列指標,所有關鍵字都在葉子結點中出現,非葉子結點作為葉子結點的索引;B+樹總是到葉子結點才命中;
B*樹:在B+樹基礎上,為非葉子結點也增加連結串列指標,將結點的最低利用率從1/2提高到2/3
