平衡二叉樹簡稱平衡樹，是由Adelson-Velskii和Landis於1962年首先提出的，所以又稱為AVL樹。他的定義很簡單，就是若一棵二叉樹的每個左右節點的高度差最多相差1，此二叉樹即是平衡二叉樹。把二叉樹的每個節點的左子樹減去右子樹定義為該節點的平衡因子。二叉平衡樹的平衡因子只能是1、0或者-1。

平衡二叉樹是對二叉搜尋樹(又稱為二叉排序樹)的一種改進。二叉搜尋樹有一個缺點就是，樹的結構是無法預料的，隨意性很大，它只與節點的值和插入的順序有關係，往往得到的是一個不平衡的二叉樹。在最壞的情況下，可能得到的是一個單支二叉樹，其高度和節點數相同，相當於一個單鏈表，對其正常的時間複雜度有O(lb n)變成了O(n)，從而喪失了二叉排序樹的一些應該有的優點。

當插入一個新的節點的時候，在普通的二叉樹中不用考慮樹的平衡因子，只要將大於根節點的值插入到右子樹，小於節點的值插入到左子樹，遞迴即可。而在平衡二叉樹則不一樣，在插入節點的時候，如果插入節點之後有一個節點的平衡因子要大於2或者小於-2的時候，他需要對其進行調整，現在只考慮插入到節點的左子樹部分（右子樹與此相同）。主要分為以下三種情況：

(1)若插入前一部分節點的左子樹高度和右子樹高度相等，即平衡因子為0，插入後平衡因子變為1，仍符合平衡的條件不用調整。

(2)若插入前左子樹高度小於右子樹高度，即平衡因子為-1，則插入後將使平衡因子變為0，平衡性反倒得到調整，所以不必調整。

(3)若插入前左子樹的高度不等於右子樹高度，即平衡因子為1或-1，則插入節點之後會使得平衡因子變為2或者-2，這樣的情況下就破壞了平衡二叉樹的結構，所以必須對其進行調整，使其平衡；

插入節點會破壞平衡的四種情況：

有四種種情況可能導致二叉查詢樹不平衡，分別為：

（1）LL：插入一個新節點到根節點的左子樹（Left）的左子樹（Left），導致根節點的平衡因子由1變為2

（2）RR：插入一個新節點到根節點的右子樹（Right）的右子樹（Right），導致根節點的平衡因子由-1變為-2

（3）LR：插入一個新節點到根節點的左子樹（Left）的右子樹（Right），導致根節點的平衡因子由1變為2

（4）RL：插入一個新節點到根節點的右子樹（Right）的左子樹（Left），導致根節點的平衡因子由-1變為-2
 

調整二叉樹首先要明白一個定義，即最小不平衡子樹。最小不平衡子樹是指以離插入節點最近、且平衡因子絕對值大於1的節點做根的子樹。

下面講解平衡二叉樹最基本的4種調整操作，調整的原則是調整後他的搜尋二叉樹的性質不變，即樹的中序遍歷是不會改變的。

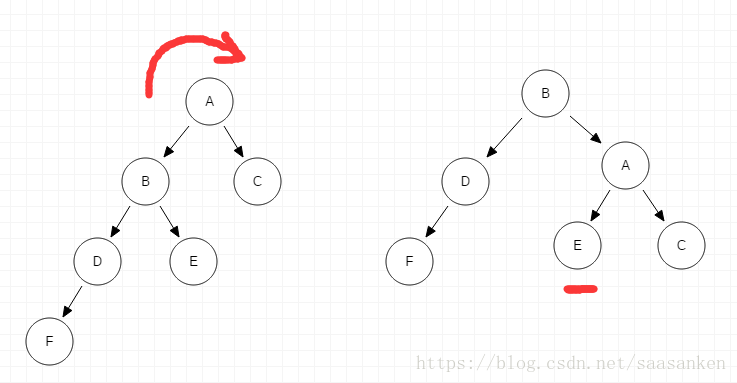
情況一：LL ->插入F節點導致失衡：

這裡失衡的是A的左右子樹，很容易就可以想到旋轉B-A鏈，值得注意的是E節點，它原先在B的右子樹，現在也依然在B的右子樹，它原先在A的左子樹，現在也依然在A的左子樹。

若插入F節點在D的右子樹處，旋轉操作依然是上圖那樣，不談。

但如果插入F節點是E的孩子就不一樣了。

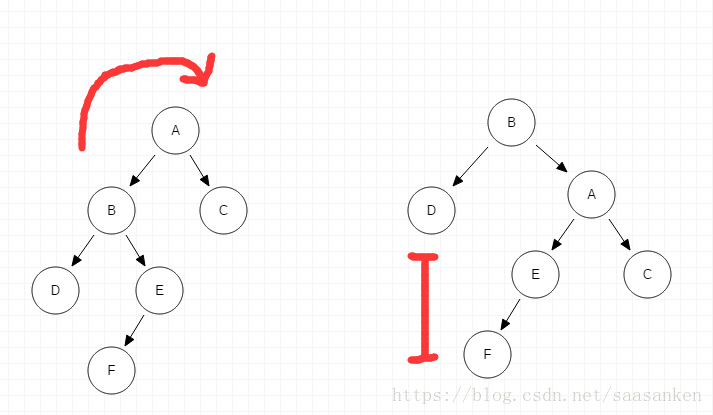
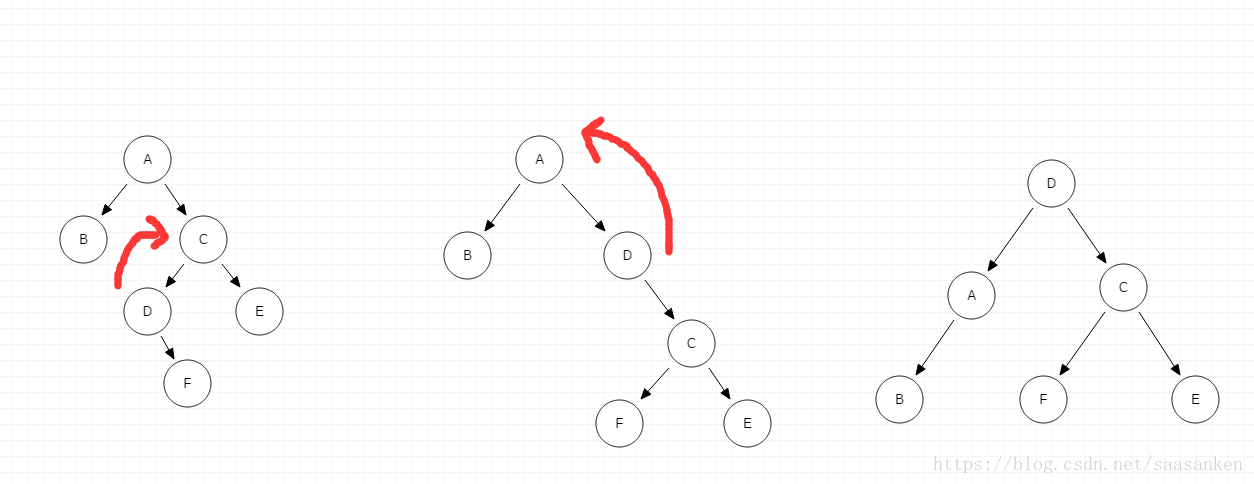
情況二：LR ->插入F節點導致失衡：

插入節點是E的孩子時，如果我們還像上面那樣旋轉B-A鏈，旋轉後的樹依然是不平衡的。事實上，這樣的旋轉使得B成為了新的根節點，而原圖中比B大的節點有4個，比B小的節點只有D，若B為根其左子樹只能為D，必定是不平衡的。

我們仔細觀察原圖，這裡E節點是很特殊的節點。首先它是實際執行了插入操作的節點，其次圖中比E小的節點有B、D、F，比E大的節點有A、C。如果能夠讓E節點做新的根節點就很好平衡了，那麼怎樣讓E節點“上位”呢？

方法是進行兩次旋轉，如下圖：

E節點恐成最大贏家……

插入節點是E的右子樹的情況與之類似，這裡給出旋轉圖：

F比E大，雙旋之後還是在E的右節點。

雙旋看圖理解起來簡單，實際實現時要注意，我們可以判斷失衡的是A節點，由A有直接關係的是B和C，那麼我們怎麼知道新插入的F節點是D的子樹還是E的子樹呢？這裡的方法是比較F節點值與B的大小，大則是E的子樹，要左-右共兩次旋轉，小則是D的子樹，要一次右旋轉。

當然還要考慮映象情況：

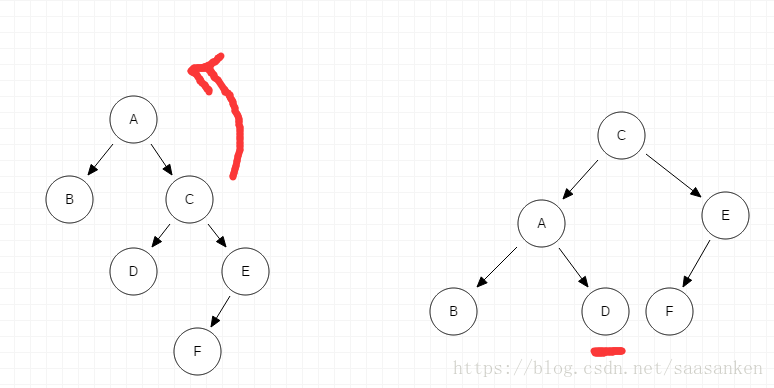
情況三：RR ->插入 F導致失衡：

進行一次左旋，關注D節點，它比C小，旋轉後依然在C的左子樹。

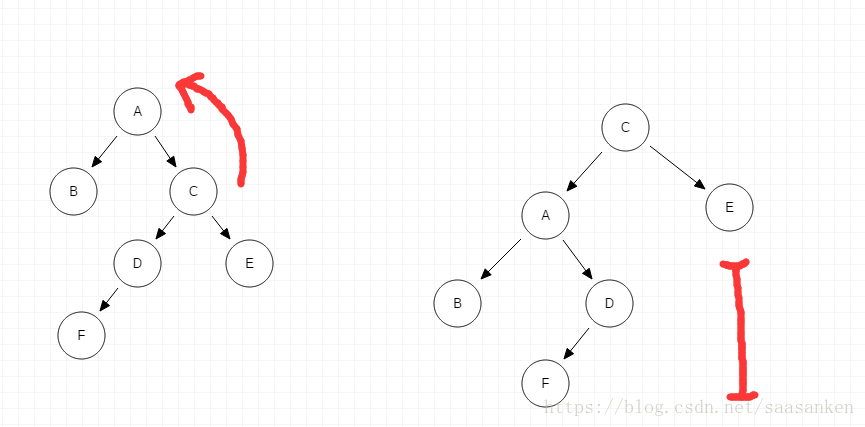
情況四：RL ->插入F導致失衡：

這時候左旋失敗，理由和之前右旋失敗類似，比C節點大的節點只有一個E，C是沒法做新的根節點的。這裡特殊的是D節點。

進行右-左兩次雙旋就可以了。D節點：爽到……

插入節點是D的右子樹情況類似，RT：

參考：https://blog.csdn.net/saasanken/article/details/80796178