在上一次的演算法討論中，我們一起學習了直接插入排序。它的原理就是把前i個長度的序列變成有序序列,然後迴圈迭代,直至整個序列都變為有序的。但是說來說去它還是一個時間複雜度為(n^2)的演算法,難道就不能再進一步把時間複雜度降低一階麼?

確實,以上幾種演算法相對於之前的O(n^2)級別的演算法真的是弱,效率可能還會差上千萬倍，但是我們不妨翻看一下歷史,你就會感覺每一種演算法的出現都是很可貴的。

一、演算法思想

希爾排序是希爾（Donald Shell）於1959年提出的一種排序演算法。希爾排序也是一種插入排序，它是簡單插入排序經過改進之後的一個更高效的版本，也稱為縮小增量排序，同時該演算法是衝破O(n2）的第一批演算法之一。

因為在1959年之前的相當長的一段時間裡,各種各樣的排序演算法無論是怎麼花樣繁多,都始終無法突破O(n^2),在當時直接插入排序已經是相當優秀的了,而排序演算法不可能突破O(n^2)的聲音成為了當時的主流。希爾排序的出現帶來了新的希望。

該方法的基本思想是：先將整個待排元素序列切割成若干個子序列（由相隔某個“增量”的元素組成的）分別進行直接插入排序，然後依次縮減增量再進行排序，待整個序列中的元素基本有序（增量足夠小）時，再對全體元素進行一次直接插入排序。由於直接插入排序在元素基本有序的情況下（接近最好情況），效率是非常高的，因此希爾排序在時間效率上比前兩種方法有較大提高。

希爾排序是基於插入排序的以下兩點性質而提出改進方法的：

• 插入排序在對幾乎已經排好序的資料操作時，效率高，即可以達到線性排序的效率。
• 但插入排序一般來說是低效的，因為插入排序每次只能將資料移動一位。

增量的選擇：在每趟的排序過程都有一個增量，至少滿足一個規則 增量關係 d[1] > d[2] > d[3] >..> d[t] = 1 (t趟排序)；根據增量序列的選取其時間複雜度也會有變化，這個不少論文進行了研究，在此處就不再深究。本文采用增量為n/2,以此遞推，每次增量為原先的1/2，直到增量為1。 

希爾排序的排序效率和選擇步長序列有直接關係，從length逐步減半，這還不算最快的希爾，有幾個增量在實踐中表現更出色，具體可以看weiss的資料結構書，同時裡面有希爾排序複雜度的證明，但是涉及組合數學和數論，希爾排序是實現簡單但是分析極其困難的一個演算法的例子。目前最好的序列是 塞奇威克（Sedgewick）的步長序列（摘自維基百科）

• 希爾（Shell）原始步長序列：N / 2，N / 4，...，1（重複除以2）
• 希伯德（Hibbard）的步長序列：1，3，7，...，2 k - 1
• 克努特（Knuth）的步長序列：1，4，13，...，（3 k - 1）/ 2
• 塞奇威克（Sedgewick） 的步長序列：1，5，19，41，109

二、演算法步驟

演算法步驟可以簡單分為：

• 用增量進行分組
• 對每組進行插入排序

舉個例子，按步長序列 [1,3,5，...] 對陣列[ 13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10 ] 進行希爾排序,首先按步長為5 進行分組，每行為一個分組得到：

13   25   45   1014   59   2794   94   7333   65   2582   23   39

然後對每行分組進行排序得到：

10   13   25   45 14   27   5973   94   9425   33   6523   39   82  

然後再按步長為3進行分組，每行為一個分組得到：
10   25   27   39   94   45 14   23   94   25   6573   13   33   59   82
對每行分組進行排序得到：
10   25   27   39   45   94 14   23   25   65   9413   33   59   73   82 

此時陣列如下所示，可以看到，元素本身已經基本有序了，此時插入排序的效率可以達到最高
[ 10 14 13 25 23 33 27 25 59 39 65 73 45 94 82 94 ]
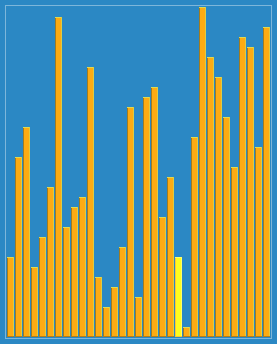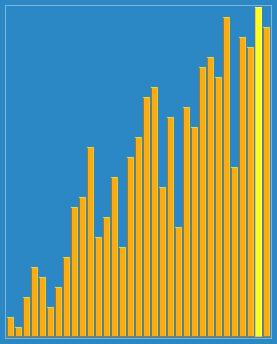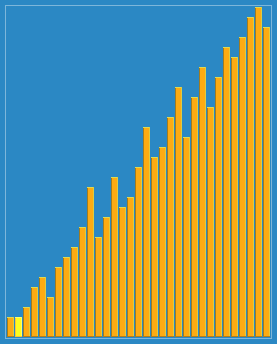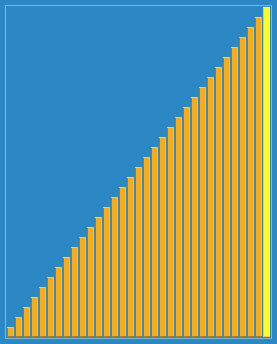
看起來 比直接分組排序多了些步驟，而實際上是讓一些小數跳過了一些比較和交換操作，直接從後面跳到了前面，從而提高了效率。下面這個動態圖形象的解釋了希爾排序的過程：

三、演算法分析

希爾排序中對於增量序列的選擇十分重要，直接影響到希爾排序的效能。我們上面選擇的增量序列{n/2,(n/2)/2...1}(希爾增量)，其最壞時間複雜度依然為O(n2)，一些經過優化的增量序列如Hibbard經過複雜證明可使得最壞時間複雜度為O(n3/2)

排序方法	時間複雜度			空間複雜度	穩定性	複雜性
	平均情況	最壞情況	最好情況
Shell 排序	O(n3/2)	O(n^2)	O(n)	O(1)	不穩定	較複雜

（上面這個我引用的圖空間複雜度有問題，原來是O(N)，我修改了，其實應該是O(1)）

對於希爾排序的一個理解，我覺得知乎上有個答主說的很好，從本質上剖析了高效演算法之所以高效的原因：

希爾能突破O(N^2)的界，可以用逆序數來理解，假設我們要從小到大排序，一個數組中取兩個元素如果前面比後面大，則為一個逆序，容易看出排序的本質就是消除逆序數，可以證明對於隨機陣列，逆序數是O(N^2)的，而如果採用“交換相鄰元素”的辦法來消除逆序，每次正好只消除一個，因此必須執行O(N^2)的交換次數，這就是為啥冒泡、插入等演算法只能到平方級別的原因，反過來，基於交換元素的排序要想突破這個下界，必須執行一些比較，交換相隔比較遠的元素，使得一次交換能消除一個以上的逆序，希爾、快排、堆排等等演算法都是交換比較遠的元素，只不過規則各不同罷了。

四、演算法實現

程式碼在VC++環境下編譯通過

/*Shell排序陣列
  version: Shell插入排序
*/


#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#ifndef N
#define N 100
#endif // N


int arr[N];

inline int Shell_Sort(int *arr)
{
    register int i, j, k, tmp;
    int incre;  //選擇一個增量，這裡我們用簡單的二分法

    for(incre = N/20; incre > 0;incre /= 2)
    { 
        for(i = incre; i < N/10; i++)
        {
            tmp = arr[i];
           // 很明顯和插排的不同就是插排這裡是j = i - 1
            j = i - incre;
            while( j >= 0 && tmp < arr[j])
            {
                arr[j + incre] = arr[j];
                j -= incre;
            }
            arr[j + incre] = tmp;

        }
    }
}

int main( int argc, int *argv[])
{
    int i;


    printf("please enter 10 numbers: \n");

    for(i = 0;i < N/10;i++)
    {
        scanf("%d", &arr[i]);
    }

    Shell_Sort(arr);

    printf("\n");
    printf("the ordered array is: \n");

    for(i = 0;i < N/10;i++)
    {
        printf("%4d", arr[i]);

    }
}

輸入：

5，13，7，26，54，8，42，33，72，41

輸出：

參考文章：