插入排序 以及其改進型 希爾排序的Java實現以及實際效能對比

簡單對插入排序和希爾排序做一個介紹，以及給出Java實現，之後簡單分析下兩者的時間複雜度，以及實際表現

插入排序：

這裡用一張圖簡單表示一下：

希爾排序：

帶有一種步長的排序，步長的最後一步總是1

可以認為普通的插入排序是希爾排序的最後一步，但因為希爾排序在最後一步前已調整好了大部分元素的順序，因此相對耗時的交換賦值操作比插入排序要少很多。

不光是在最後一步，從總體來看希爾排序比插入排序快就快在交換賦值操作要少。

在稍後的測試中可以看到，在資料量超過10000的時候，插入排序的效率遠遠不如希爾排序

希爾排序的具體原理及實現參考：

希爾排序

插入排序和希爾排序的Java實現

插入排序：

package com.ryo.algorithm.sort;

/**
 * 插入排序
 * @author shiin
 */
public class InsertionSort implements Sort{
	
	@Override
	public int[] sort(int[] arr) {
		int temp ;
		int j;
		for(int i=1 ;i<arr.length ;i++) {
			temp = arr[i];
			j = i-1;
			//這裡要寫成強且 否則當j=-1時第二個判斷將會丟擲outofindex異常
			while(j > -1 && arr[j] > temp) {
				arr[j+1] = arr[j];
				j--;
			}
			arr[j+1] = temp;
		}
		return arr;
	}

}
 

希爾排序：

package com.ryo.algorithm.sort;

/**
 * 這裡預設陣列的長度將大於37
 * @author shiin
 *
 */
public class ShellSort implements Sort{
	
	//步長序列
	private int[] steplist = {373,181,83,37,17,7,3,1};

	@Override
	public int[] sort(int[] arr) {
		//輸入陣列長度
		int len = arr.length;
		//進行子排序次數
		int times = 0;
		//當前步長
		int step;
		//臨時儲存的變數
		int temp;
		//臨時儲存的索引
		int m;
		for(;times < steplist.length ;times++) {
			step = steplist[times];
			//這裡i相當於是一個偏移量 最大偏移不能超過步長
			for(int i=0 ;i<step ;i++) {
				//j,j+step,j+2*step......為被分到一組的下標
				//這裡開始和直接插入排序相似，可以認為直接插入排序的step為1
				for(int j=i ;j<len &(j+step)<len;j=j+step) {
					temp = arr[j+step];
					m = j;
					while(m > -1 && arr[m] > temp) {
						arr[m+step] = arr[m];
						m = m-step;
					}
					arr[m+step] = temp;
				}
			}
		}
		return arr;
	}
}
 

用於測試的類：

packagecom.ryo.algorithm.sort;
 
import com.ryo.algorithm.util.Util;
 
public class DoSort {
    
    private int[] result = new int[20000];
 
    public static void main(String[] args) {
       DoSort ds = new DoSort();
       long before = System.currentTimeMillis();
       
       //在這一行更換需要測試的方法
       ds.testShellSort();
       
       long after = System.currentTimeMillis();
       for(intn : ds.getResult()) {
           System.out.println(n);
       }
       System.out.println("total time : "+(after-before)+"ms");
    }
    
    public DoSort() {
       for(inti=0 ;i<result.length ;i++) {
           //這裡是已寫好的隨機建立0-10000隨機數的方法
           result[i] = Util.random();
       }
    }
    
    public void testInsertionSort() {
       new InsertionSort().sort(result);
    }
    
    public void testShellSort() {
       new ShellSort().sort(result);
    }
    
    public int[] getResult() {
       return this.result;
    }
 
}

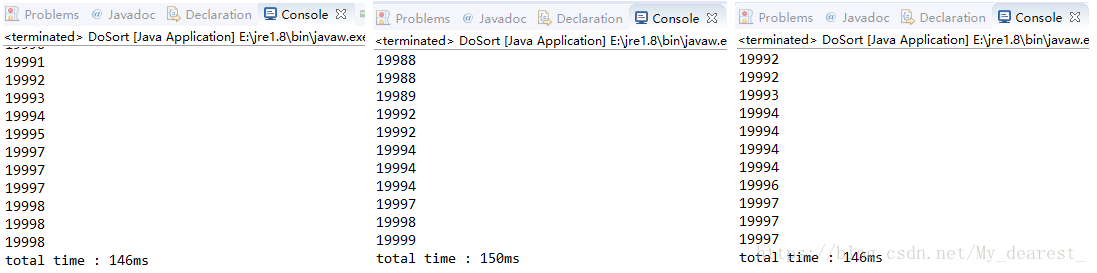
效能對比：

測試環境：Jdk 1.8.0_161    eclipse Version: Oxygen.3a Release (4.7.3a)

測試資料：陣列長度為20000，存有0-20000隨機整數， 事先跑數次使得執行時間穩定，再取三次執行的平均值 ，初始化等額外操作均不在計時範圍內

執行時間結果：

插入排序

平均時間：147ms

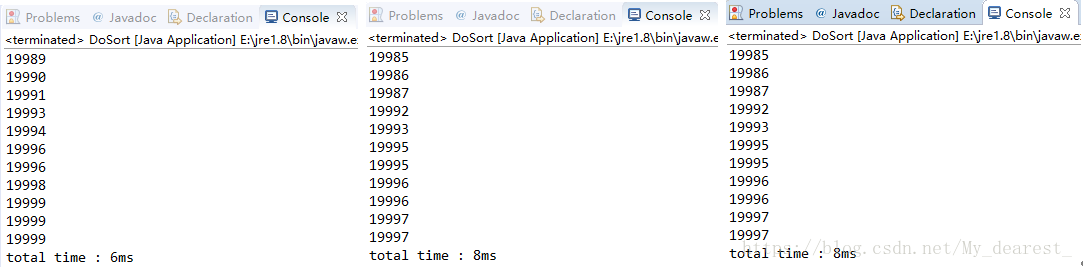
希爾排序

平均時間：7ms

實際上因為這裡取的步長最大才為373，多取幾個步長執行時間還會更小，步長的取值直接影響到希爾排序的效率，且影響非常大

這裡在private int[] steplist ={373,181,83,37,17,7,3,1};的基礎上附加一個733和1607，再跑起來發現時間基本可以穩定在6ms

由這裡的結果對比可以看到，在資料量超過10000的時候，希爾排序的效率遠遠大於直接插入排序，若資料量繼續增大，插入排序所需要的時間將增長的更快。

關於直接插入排序和希爾排序的時間複雜度

直接插入排序的平均時間複雜度為O(n^2)，最好情況下（即已排好序）時間複雜度為O(n)，最差情況下（即逆序排列）的時間複雜度為O(n^2)

希爾排序的平均時間複雜度在選擇較好的步長時應該能接近O(n^1.3)，最壞和最優的時間複雜度和直接插入排序相同

由於希爾排序的效率跟程式選擇的步長緊密相關，關於希爾排序步長選擇的研究其實是一個數學難題

在本程式中對比實際效率：

理論效率倍數：20000^2 / 20000^1.3 = 1025

實際效率倍數：147 / 7 = 21

1025 >> 21

由於1025只是理論效率倍數，但由於時間複雜度的計算中只包括了主要的耗時操作，一些非關鍵操作直接認為耗時為0，且還有Java環境、記憶體存取等影響，造成了數值偏差較大

但我們依然可以看到兩種演算法實際效率之間存在較大的差距