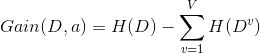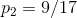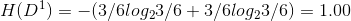最經典的決策樹演算法有ID3、C4.5、CART，其中ID3演算法是最早被提出的，它可以處理離散屬性樣本的分類，C4.5和CART演算法則可以處理更加複雜的分類問題，本文重點介紹ID3演算法。

1、決策樹基本流程

決策樹 (decision tree) 是一類常見的機器學習方法。它是對給定的資料集學到一個模型對新示例進行分類的過程。下圖所示為一個流程圖的決策樹，長方形代表判斷模組（decision block），橢圓形代表終止模組（terminating block），表示已經得出結論，可以終止執行。從判斷模組引出的左右箭頭稱作分支（branch），可以達到另一個判斷模組或終止模組。

決策過程是基於樹

結構來進行決策的。如下圖，首先檢查郵件域名地址，如果地址為myEmployer.com，則將其分類為“無聊時需要閱讀的郵件”。否則，則檢查郵件內容裡是否包含單詞“曲棍球”，如果包含則歸類為“需要及時處理的朋友郵件”，如果不包含則歸類到“無需閱讀的垃圾郵件”

顯然，決策過程的最終結論對應了我們所希望的判定結果，例如"需要閱讀"或"不需要閱讀”。

決策過程中提出的每個判定問題都是對某個屬性的"測試"，如郵件地址域名為？是否包含“曲棍球”？

每個測試的結果或是匯出最終結論，或是匯出進一步的判定問題，其考慮範國是在上次決策結果的限定範圍之內，例如若郵件地址域名不是myEmployer.com之後再判斷是否包含“曲棍球”。

一般的，決策樹包含一個根節點、若干個內部節點和若干個葉節點。根節點包含樣本全集；葉節點對應於決策結果，例如“無聊時需要閱讀的郵件”。其他每個結點則對應於一個屬性測試；每個節點包含的樣本集合根據屬性測試的結果被劃分到子結點中。

顯然，決策樹的生成是一個遞迴過程.在決策樹基本演算法中，有三種情形會導致遞迴返回: (1)當前結點包含的樣本全屬於同一類別，無需劃分; (2)當前屬性集為空，或是所有樣本在所有屬性上取值相同，無法劃分; (3)當前結點包含的樣本集合為空，不能劃分。

---

2、劃分選擇

決策樹演算法的關鍵是如何選擇最優劃分屬性。一

般而言，隨著劃分過程不斷進行，我們希望決策樹的分支結點所包含的樣本儘可能屬於同一類別，即結點的"純度" (purity)越來越高。

（1）資訊增益

資訊熵

"資訊熵" (information entropy)是度量樣本集合純度最常用的一種指標，定義為資訊的期望。假定當前樣本集合 D 中第 k 類樣本所佔的比例為

 ,則 D 的資訊熵定義為：

                                                                             
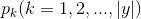
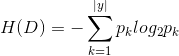
H(D)的值越小，則D的純度越高。

---

資訊增益

                                                                 
一般而言，資訊增益越大，則意味著使周屬性 來進行劃分所獲得的"純度提升"越大。因此，我們可用資訊增益來進行決策樹的劃分屬性選擇，資訊增益越大，屬性劃分越好。

---

以西瓜書中表 4.1 中的西瓜資料集 2.0 為例，該資料集包含17個訓練樣例，用以學習一棵能預測設剖開的是不是好瓜的決策樹.顯然，。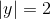

在決策樹學習開始時，根結點包含 D 中的所有樣例，其中正例佔 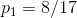，反例佔 

資訊熵計算為：

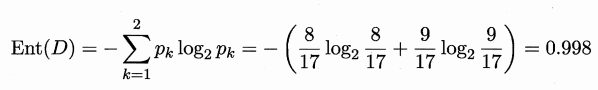
我們要計算出當前屬性集合{色澤，根蒂，敲聲，紋理，臍部，觸感}中每個屬性的資訊增益。以屬性"色澤"為例，它有 3 個可能的取值: {青綠，烏黑，淺自}。若使用該屬性對 D 進行劃分，則可得到 3 個子集，分別記為：D1 (色澤=青綠)， D2 (色澤2=烏黑)， D3 (色澤=淺白)。

子集 D1 包含編號為 {1，4，6，10，13，17} 的 6 個樣例，其中正例佔 p1=3/6 ，反例佔p2=3/6； 

D2 包含編號為 {2，3，7，8， 9，15} 的 6 個樣例，其中正例佔 p1=4/6 ，反例佔p2=2/6； 

D3 包含編號為 {5，11，12，14，16} 的 5 個樣例，其中正例佔 p1=1/5 ，反例佔p2=4/5；

根據資訊熵公式可以計算出用“色澤”劃分之後所獲得的3個分支點的資訊熵為：

                                                            

根據資訊增益公式計算出屬性“色澤”的資訊增益為（Ent表示資訊熵）：

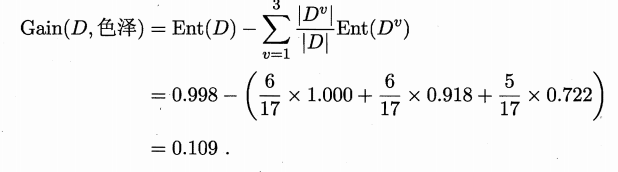
類似的，可以計算出其他屬性的資訊增益：

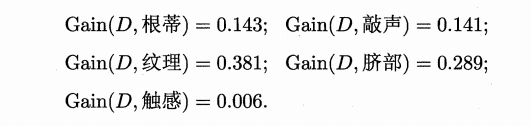
顯然，屬性"紋理"的資訊增益最大，於是它被選為劃分屬性。圖 4.3 給出了基於"紋理"對根結點進行劃分的結果，各分支結點所包含的樣例子集顯示在結點中。

然後，決策樹學習演算法將對每個分支結點做進一步劃分。以圖 4.3 中第一個分支結點( "紋理=清晰" )為例，該結點包含的樣例集合 D 1 中有編號為 {1, 2, 3, 4, 5, 6, 8, 10, 15} 的 9 個樣例，可用屬性集合為{色澤，根蒂，敲聲，臍部 ，觸感}。基於 D1計算出各屬性的資訊增益：

"根蒂"、 "臍部"、 "觸感" 3 個屬性均取得了最大的資訊增益，可任選其中之一作為劃分屬性.類似的，對每個分支結點進行上述操作，最終得到的決策樹如圈 4.4 所示。

---

3、剪枝處理

剪枝 (pruning)是決策樹學習演算法對付"過擬合"的主要手段。決策樹剪枝的基本策略有"預剪枝" (prepruning)和"後剪枝 "(post"
pruning) [Quinlan, 1993]。

預剪枝是指在決策樹生成過程中，對每個結點在劃分前先進行估計，若當前結點的劃分不能帶來決策樹泛化效能提升，則停止劃
分並將當前結點標記為葉結點；

後剪枝則是先從訓練集生成一棵完整的決策樹，然後自底向上地對非葉結點進行考察，若將該結點對應的子樹替換為葉結點能帶來決策樹泛化效能提升，則將該子樹替換為葉結點。

（本文主要參考周志華老師的《機器學習》和Peter Harrington的《機器學習實戰》）