演算法第五章 | 回溯演算法
演算法第五章 | 回溯演算法
一、 回溯演算法
回溯法有“通用的解題法”之稱。可以系統地搜尋一個問題的所有解或任一解,是一個既帶有系統性又帶有跳躍性的搜尋演算法。
它在問題的解空間樹中,按深度優先策略,從根節點出發搜尋解空間樹。演算法搜尋至解空間樹的任一結點時,先判斷該結點是否包含問題的解。如果肯定不包含,則跳過對以該結點為根的子樹的搜尋,逐層向其祖先結點回溯。否則,進入該子樹,繼續按深度優先策略搜尋。回溯法求問題的所有解時,要回溯到根,且根結點的所有子樹都已被搜尋遍才結束。回溯法求問題的一個解時,只要搜尋到問題的一個解就可結束。
這種以深度優先方式系統搜尋問題的解的搜尋問題解的演算法稱為回溯法,它適用於組合數較大的問題。
1.問題的解空間
用回溯法解問題時,應明確定義問題的解空間,問題的解空間至少應包含問題的一個(最優)解。
定義了問題的解空間後,還應將解空間很好地組織起來,使得能用回溯法方便地搜尋整個解空間。通常將解空間組織成樹或圖的形式。
例:n=3時的0-1揹包問題,可用一棵完全二叉樹表示其解空間。
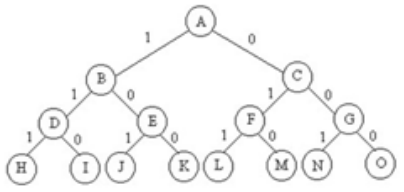
(圖) 0-1揹包的解空間樹
2.回溯法的基本思想
確定瞭解空間的組織結構後,回溯法從開始結點(根結點)出發,以深度優先方式搜尋整個解空間。這個開始結點成為活結點,同時也成為當前的擴充套件結點。在當前的擴充套件結點處,搜尋向縱深方向移至一個新節點。該新節點成為新的活結點,併成為當前擴充套件結點。如果在當前的擴充套件結點出不能再向縱深方向移動,則當前擴充套件就成為死結點。此時,應往回移動(回溯)至最近的一個活結點處,並使這個活結點成為當前的擴充套件結點。回溯法以這種工作方式遞迴地在解空間中搜索,直至找到所要求的解或解空間中已無活點為止。
3.約束函式
回溯法搜尋解空間時,通常採用兩種策略避免無效搜尋,提高回溯法的搜尋效率。
其一是用約束函式在擴充套件結點處剪去不滿足約束的子樹。
其二是用限界函式剪去得不到最優解的子樹。
這兩類函式統稱為剪枝函式。
二、 “子集和”問題的解空間結構和約束函式
1.問題描述:設集合S={x1,x2,…,xn}是一個正整數集合,c是一個正整數,子集和問題判定是否存在S的一個子集S1,使S1中的元素之和為c。試設計一個解子集和問題的回溯法。
2.解空間結構:
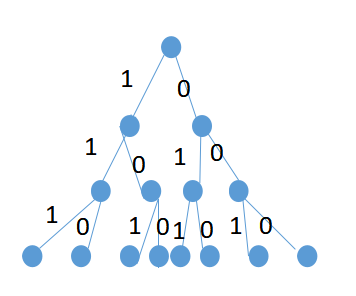
(圖)解空間結構
3.約束函式:
If (c < sum) {v[p] = false; sum-= data[p];}
4.具體程式碼如下:
bool traceback(int n) {
int p = 0, sum = 0;
while (p >= 0) {
if (!v[p]) {
v[p] = true;
sum += data[p];
if (c == sum)
return true;
else if (c < sum) {
v[p] = false;
sum -= data[p];
}
p++;
}
if (p >= n) {
while (v[p - 1]) {
p--;
v[p] = false;
if (p<1) return false;
}
while (!v[p - 1]) {
p--;
if (p<1) return false;
}
sum -= data[p - 1];
v[p - 1] = false;
}
}
return false;
}
三、 學習過程中遇到的問題及結對程式設計情況
1.實現回溯演算法的能力有待提高。
2.未能熟練掌握套子集數模板的能力。
3.與隊友交流過模板及剪枝的問題。
