1 - 引言

空間濾波是影象處理領域應用廣泛的主要工具之一。這裡我們主要討論怎樣使用空間濾波來增強影象。

2 - 平滑空間濾波器

平滑濾波器用於模糊處理和降低噪聲。模糊處理經常用於預處理任務中，例如在目標提取之前去除影象中的一些瑣碎細節。

2.1 - 平滑線性濾波器

平滑線性空間濾波器的輸出（響應）是包含在濾波器過濾核中畫素的簡單平均值，也成為均值濾波。

這種處理的結果降低了影象灰度的“尖銳”變化。

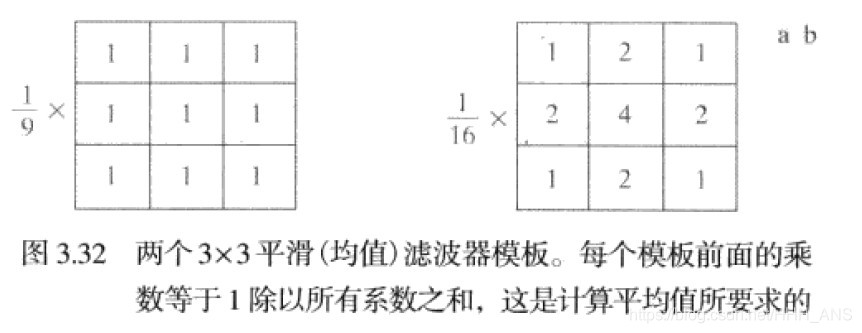
這種濾波器(3x3)一般分為兩種

• 第一種為標準像素平均值 $R$
  = 1 9 ∑ i = 1
  9 z i R = \frac{1}{9}\sum_{i=1}^9z_i
• 第二種為加權平均 $g$
  ( x , y ) = ∑ s = − a a ∑ t = − b b w ( s , t ) f ( x + s , y + t ) ∑ s = − a a ∑ t = − b b w ( s , t ) g(x,y)=\frac{\sum_{s=-a}^a\sum_{t=-b}^bw(s,t)f(x+s,y+t)}{\sum_{s=-a}^a\sum_{t=-b}^bw(s,t)}

import cv2
import numpy as np

img = cv2.imread('images/cat.jpg')
cv2.imshow('images',img)
"""
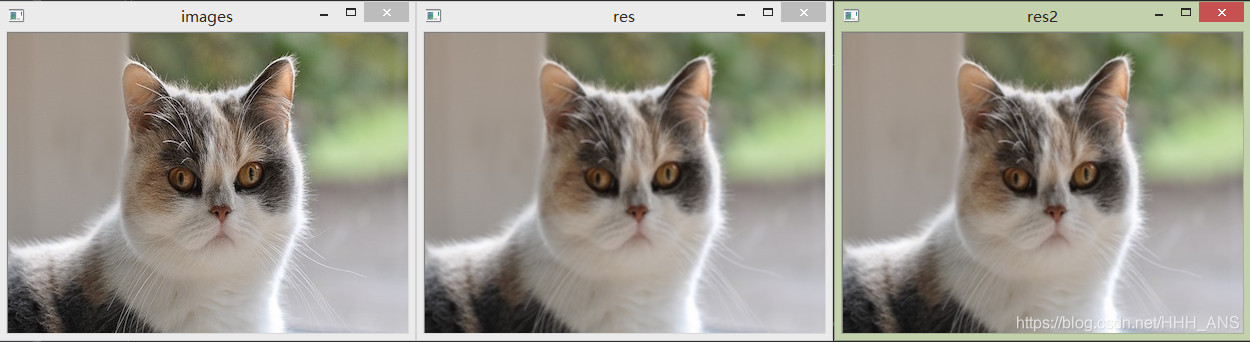
blur—影象均值平滑濾波
函式原型：blur(src, ksize, dst=None, anchor=None, borderType=None)
src：影象矩陣
ksize：濾波視窗尺寸
"""
res = cv2.blur(img, (3, 3))
cv2.imshow('res', res)
"""
GaussianBlur—影象高斯平滑濾波
函式原型：GaussianBlur(src, ksize, sigmaX, dst=None, sigmaY=None, borderType=None)
src：影象矩陣
ksize：濾波視窗尺寸
sigmaX：標準差

"""
res2 = cv2.GaussianBlur(img,(3,3),0)
cv2.imshow('res2', res2)
cv2.waitKey()

（可以用來磨皮哦，手動滑稽）

2.2 - 非線性濾波器

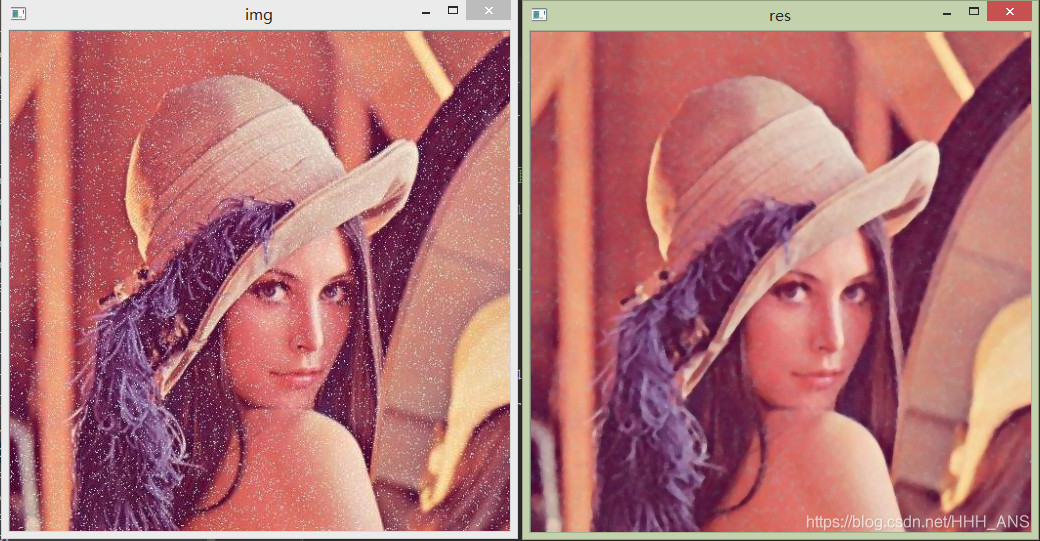
這種濾波器的響應一濾波器過濾核中畫素的排序為基礎，然後使用統計排序的結果決定代替中心畫素的值。這一類最知名的濾波器是中值濾波器，正如其名，它是將畫素領域內灰度的終止代替該畫素的值。中值濾波器對處理脈衝噪聲非常有效，這種噪聲也成為椒鹽噪聲。

import cv2
import numpy as np

img = cv2.imread('images/lena_1.jpg')
cv2.imshow('img', img)
"""
medianBlur—影象中值濾波
函式原型：medianBlur(src, ksize, dst=None)
src：影象矩陣
ksize：濾波視窗尺寸

"""
res = cv2.medianBlur(img, 5)
cv2.imshow('res', res)
cv2.waitKey()

3 - 銳化空間濾波器

銳化處理的主要目的是突出灰度的過度部分。

3.1 - 使用二階微分進行影象銳化——拉普拉斯運算元

一個二維影象函式f(x,y)的拉普拉斯運算元定義為
$\triangledown ^2f=\frac{\partial^2 f}{\partial x^2}+\frac{\partial^2 f}{\partial y^2}$
離散形式為
$\triangledown ^2f=f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)-4f(x,y)$
我們可以發現這正好可以寫成濾波器：

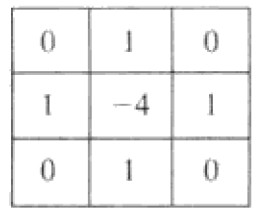
由於拉普拉斯是一種微分運算元，因此其應用強調的是影象中灰度的突變，並不強調灰度級緩慢變化的區域。將原影象和拉普拉斯影象疊加在一起的簡單方法，可以復原背景特性並保持拉普拉斯銳化處理的效果。

如果所使用的定義具有負的中心繫數，那麼必須將原影象減去拉普拉斯變換後的影象而不是加上它，從而得到銳化的結果。

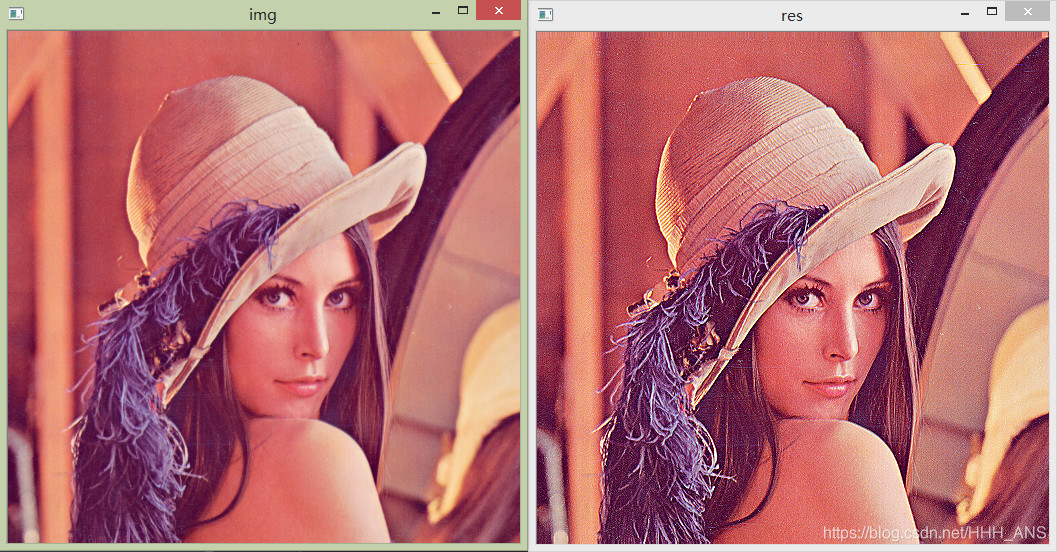
import cv2
import numpy as np
img = cv2.imread('images/lena.jpg')
cv2.imshow('img',img)
kernel = np.array([[0, -1, 0], [-1, 5, -1], [0, -1, 0]], np.float32)
#kernel = np.array([[-1,-1,-1], [-1,9,-1], [-1,-1,-1]])
dst = cv2.filter2D(img, -1, kernel=kernel)
cv2.imshow('res',dst)
cv2.waitKey(0)

3.2 - 非銳化巖壁和高提升濾波

在印刷和出版界已用了多年的影象銳化處理過程是從原影象中減去一副非銳化（平滑過）版本。
非銳化掩蔽的處理過程為：

1. 模糊原影象
2. 從原影象中減去模糊影象（產生的差值影象成為模板）
3. 將模板加到原影象上

(這個較為簡單就不進行試驗了)

3.3 - 使用一階微分對（非線性）影象銳化——梯度

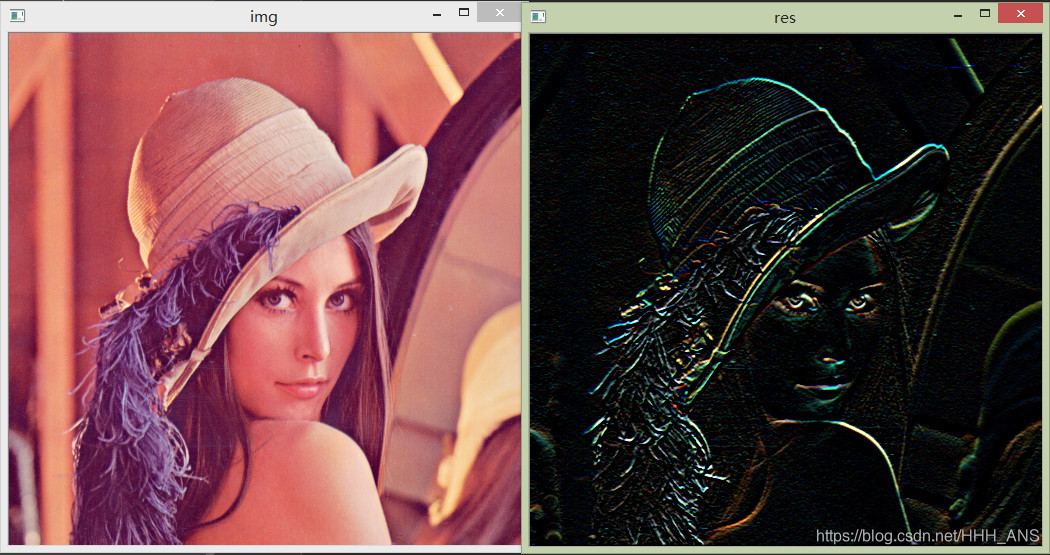
使用梯度銳化影象的運算元叫Sobel運算元
Sobel運算元依然是一種過濾器
影象的每一個畫素的橫向及縱向梯度近似值可用以下的公式結合，來計算梯度的大小。
$G = \sqrt{G_x^2+G_y^2}$

Sobel運算元包含兩組3x3的矩陣，分別為橫向及縱向模板，將之與影象作平面卷積，即可分別得出橫向及縱向的亮度差分近似值。實際使用中，常用如下兩個模板來檢測影象邊緣。
$G_x=\begin{bmatrix} -1 &0 &1 \\ -2 & 0 & 2\\ -1 &0 & 1 \end{bmatrix} G_y=\begin{bmatrix} 1 &2 &1 \\ 0 & 0 & 0\\ -1 &-2 & -1 \end{bmatrix}$

# coding=utf-8
import cv2


img = cv2.imread("images/lena.jpg")
cv2.imshow('img',img)
"""
Sobel函式
Sobel(src, ddepth, dx, dy, dst=None, ksize=None, scale=None, delta=None, borderType=None)
前四個是必須的引數：
第一個引數是需要處理的影象；
第二個引數是影象的深度，-1表示採用的是與原影象相同的深度。目標影象的深度必須大於等於原影象的深度；
第三和第四：dx和dy表示的是求導的階數，0表示這個方向上沒有求導，一般為0、1、2。
其後是可選的引數
"""
x = cv2.Sobel(img, -1, 0, 1)
cv2.imshow('res',x)
cv2.waitKey(0)