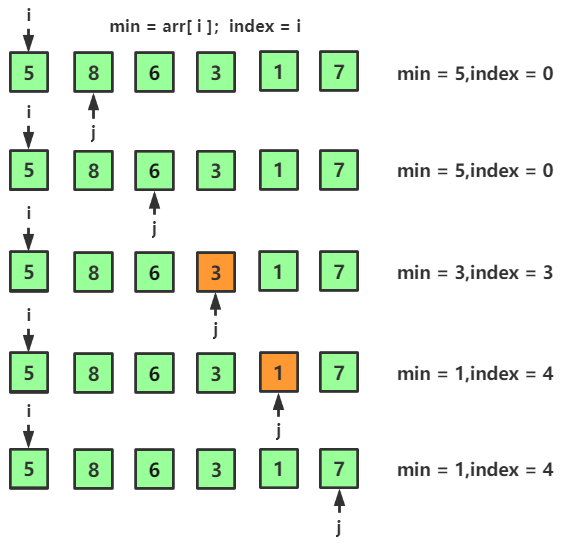
# 選擇排序 ## 前言 **原理：**每次迴圈對比找出最小/大值，將最值的元素交換至左側 **思想：**直接選擇排序（Straight Select Sort）演算法思想：第一趟從n個元素的資料序列中選出關鍵字最小/大的元素並放在最前/後位置，下一趟從n-1個元素中選出最小/大的元素並放在最前/後位置。以此類推，經過n-1趟完成排序 **案例分析**： 1、初始的無序數列 `{5,8,6,3,1,7}`，希望對其升序排序 2、按照思路分析：  內層迴圈經過一輪對比後找到最小值，`min = 1`，下標為` index = 4`；交換位置  ## 程式碼實現 ### 第 1 版程式碼 ```java public static void straightSelectSort(int[] arr){ //i不需要 = 陣列最尾部元素，因為後面沒有值對比了 for (int i = 0; i < arr.length - 1; i++) { //設定每次迴圈的起始點為最小/大值 int min = arr[i]; //記錄下最小/大值的下標 int index = i; for (int j = i + 1; j < arr.length; j++) { //升序排序>,降序排序< if (min > arr[j]){ min = arr[j]; index = j; } } //一輪對比完成後，將預設的最小值賦予到找到的最值下標位置 arr[index] = arr[i]; //把找到的真實最值放到前面 arr[i] = min; } } ``` 這裡其實有可能出現預設的最小值其實就是真正的最小值，所以一輪內層迴圈下來，是沒有交換資料，可以新增哨兵，如果沒有找到最小值，就不進行值的交換，減少交換次數。 ### 第 2 版程式碼 ```java public static void straightSelectSort(int[] arr){ //i不需要 = 陣列最尾部元素，因為後面沒有值對比了 for (int i = 0; i < arr.length - 1; i++) { //設定每次迴圈的起始點為最小/大值 int min = arr[i]; //記錄下最小/大值的下標 int index = i; //哨兵，記錄是否找到最值，預設false boolean isSwap = false; for (int j = i + 1; j < arr.length; j++) { //升序排序>,降序排序< if (min > arr[j]){ min = arr[j]; index = j; //找到最值，設定為true isSwap = true; } } if (isSwap){ //一輪對比完成後，將預設的最小值賦予到找到的最值下標位置 arr[index] = arr[i]; //把找到的真實最值放到前面 arr[i] = min; } } } ``` **直接選擇排序演算法複雜度分析：** 如果陣列中有**n個元素 第1輪迴圈是arr[0] 和arr[1] ...arr[n-1] 進行比較，次數為n-1 次，arr[0]放最值。 第2輪迴圈是arr[1] 和 arr[2]...arr[n-1] 進行比較，次數為n-2次，arr[1]放第二個最值。 所以不難得出它的比較的次數是n-1 + n-2 + n-3 + ....1 = n*（n-1）/2 。 時間複雜度為 = n^2/2- n/2 = n^2 ,**O（n^2）**。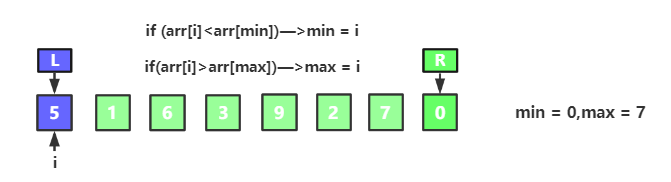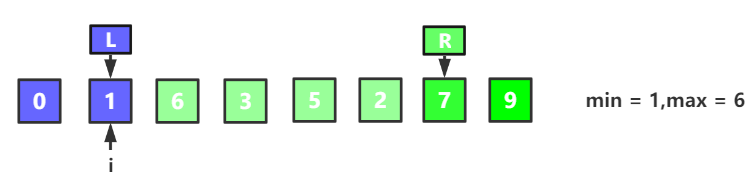 ## 演算法升級 ### 分析 直接選擇排序每一次查詢只是找出最小值，可以這麼改進，查詢最小值的同時，找到一個最大值，然後將兩者分別放在它們應該出現的位置，這樣遍歷的次數就會減少，同時新增哨兵，如果沒有找到最值，不發生交換 以新的無序數列 `{5,1,6,3,9,2,7,0}`為例，按照上面的分析，初始狀態如下：  排序過程如下：  交換最值，將最小值放到`arr[left]`,最大值放到`arr[right]`，同時`left++，right--`；準備下一輪迴圈，第一輪結果如下：  演算法注意點： (1) 第二輪開始對比前，我們可以發現，此時`arr[left]`與`arr[right]`恰好是此輪的最值，因此應該加上哨兵，對此情況，內迴圈走完後，不進行值交換，判斷條件：`min == right && max == left`  (2) 特別注意的地方：第三輪迴圈後，可以發現的點是，`left = 2,right = 5`,而結果是`min = 5,max = 2`,仔細看你就發現了，`left`與`min`對應，而`max`與`right`對應，結果是值反面的的，所以在進行值交換的時候，進行一次就可以了，否則交換兩次，就變成了巴黎鐵塔翻過來又翻回去了，判斷條件：`min == right && max == left`  ### 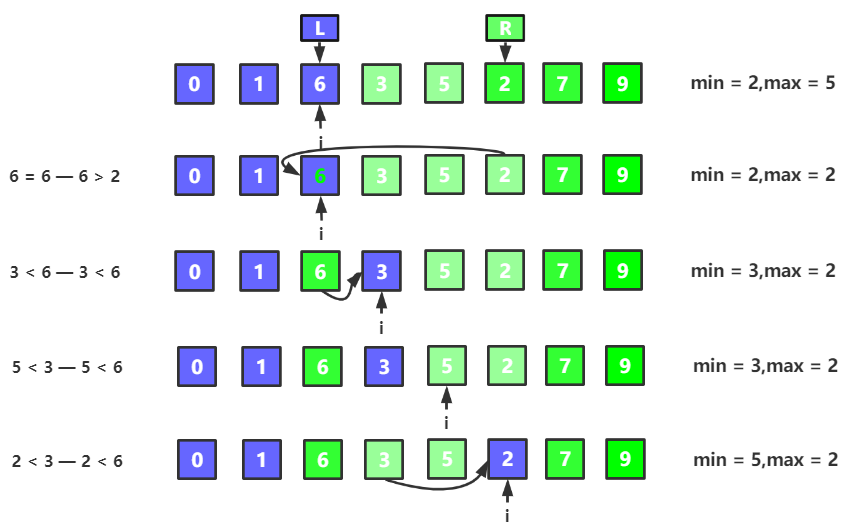進化版程式碼 ```java public static void betterSelectSort(int[] arr) { //left指標指向無序邊界起點，right指標指向終點，temp用作臨時變數交換值 int left,right,temp; //預設指向無序列表起點 left = 0; //預設指向無序列表終點 right = arr.length - 1; //記錄每輪找到的最小值的下標 int min = left; //記錄每輪找到的最大值的下標 int max = right; //當right >= left時，列表已經有序 //記錄迴圈的次數 int index = 0; while(left < right) { min = left; //每輪開始前，預設無序列表起點為最小值 max = right; //每輪開始前，預設無序列表終點為最大值 //指標i從左往右掃描，找出最小值，最大值 for (int i=left; i<=right; i++) { if