傳送門

題面：

J. The Volcano Eruption

time limit per test

5.0 s

memory limit per test

64 MB

input

standard input

output

standard output

"The volcano erupted!". Shouted Shahhoud, as he was attempting to wake Saeed up.

"You need to save Noor, he is trapped in the lab next to the volcano!". Shahhoud said.

You can picture the road between the base and the lab as a rectangle whose bottom left corner is at (0, 0) and top right corner is at (W, L). There are n holes filled with lava from the volcano. The ith hole is a circle whose center is at coordinates (xi, yi) and has a radius of ri. The holes may intersect to make larger holes.

Saeed Starts his mission at any point on the bottom side of the rectangle ( any point (0...W, 0)), and has to reach any point on the top side of the rectangle ( any point (0...W, L)), in order to save Noor.

None of the holes intersect with the bottom or the top sides of the rectangle ( the starting and finishing line).

Saeed can take special suits in his anti-lava backpack. Each special suit allows him to swim in one or more intersecting holes (once he goes out of the lava onto the street, he has to throw away the suit). Saeed must stay inside the street at all times. Please note that if two holes are touching each other by the border, then Saeed can't walk from between them without wearing a special suit.

What is the minimum number of suits Saeed has to take with him in order to reach the lab and save Noor?

Input

The first line contains a single integer T, the number of test cases. The first line of each test case contains 3 integers N,W, and L. The number of holes, the width, and the length of the rectangle. (1 ≤ N ≤ 1000) (1 ≤ W, L ≤ 109) Each of the following N lines contain 3 integers (0 ≤ xi ≤ W), (0 < yi < L), and (1 ≤ ri ≤ 109), the coordinates and radius of the ith hole. It's guaranteed that none of the holes intersect with the bottom or the top sides of the rectangle ( the starting and finishing line).

Output

For each test case, output a single line containing a single integer, the minimum number of suits Saeed must take with him to save Noor.

Example

input

Copy

1
5 5 18
4 2 1
2 12 3
4 6 2
2 6 1
1 7 1

output

Copy

2

Note

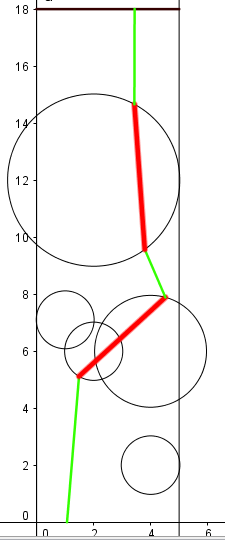
The figure below shows a possible solution for the sample.

題意：

    有一個長度為L，寬度為W的長方形區間。一共有n個圓，這n個圓可能兩兩相交，當你進入圓的區域的時候，你需要換一次衣服；而當你走出圓的領域的時候，你也需要換一次衣服。現在問你，在不能走出長方形區間的前提下，你最少需要換多少次衣服。

題目分析：

    拿到題目一看，貌似需要處理一堆圓相交的問題，貌似處理起來非常困難。

    但是如果我們再深入觀察的話，我們可以發現，對於一個圓，倘若它恰好在長方形區間內部（與長方形沒有交點），則我們可以從兩邊繞過這塊區間。因此，當且僅當存在一個圓，它的最左端覆蓋掉長方形左邊，最右端覆蓋掉長方形右邊，此時，我們必須經過該圓。因此我們只需要處理出左右邊界的情況即可。

    而因為可能存在多個圓相交的情況，此時，我們可以將相交的圓看成一個整體，用並查集對這一塊區間進行維護，最後處理一下左右邊界情況統計答案即可。

程式碼：

#include <bits/stdc++.h>
#define maxn 1005
using namespace std;
typedef long long ll;
struct Node{
    ll x,y,r;
}q[maxn];
bool Intertion(Node a,Node b){
    ll tmp=(a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y);
    ll rr=(a.r+b.r)*(a.r+b.r);
    if(tmp>rr) return 0;
    else return 1;
}
int Far[maxn];
int Find_F(int x){//並查集
    if(Far[x]==x) return x;
    else return Far[x]=Find_F(Far[x]);
}
void unite(int x,int y){
    x=Find_F(x),y=Find_F(y);
    if(x==y) return ;
    else Far[x]=y;
}
int Left[maxn],Right[maxn];//左邊界和右邊界的情況
void init(int n){
    for(int i=0;i<=n;i++){
        Far[i]=i;
        Left[i]=Right[i]=0;
    }
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--){
        ll n,w,l;
        scanf("%lld%lld%lld",&n,&w,&l);
        init(n);
        for(int i=0;i<n;i++){
            scanf("%lld%lld%lld",&q[i].x,&q[i].y,&q[i].r);
        }
        for(int i=0;i<n;i++){
            for(int j=0;j<i;j++){//用並查集去維護相交的圓
                if(Intertion(q[i],q[j])) unite(i,j);
            }
        }
        for(int i=0;i<n;i++){//分別維護左右邊界
            if(q[i].x-q[i].r<=0) Left[Find_F(i)]=1;
            if(q[i].x+q[i].r>=w) Right[Find_F(i)]=1;
        }
        int ans=0;
        for(int i=0;i<n;i++){//如果左右邊界都被某個圓集合覆蓋，則增加答案
            if(Find_F(i)==i&&Left[Find_F(i)]==1&&Right[Find_F(i)]==1) ans++;
        }
        printf("%d\n",ans);
    }
}