光照不均勻影象分割技巧2——頂帽變換和底帽變換
本文章由wikiwen撰寫,轉載請註明出處。
文章連結:http://blog.csdn.net/kk55guang2/article/details/78490069
前言
上篇文章介紹了通過分塊閾值的技巧解決光照不均勻影象分割出錯的問題,像大多數問題一樣,解決思路是多種多樣的,本文將介紹另外一種形態學方法——頂帽變換和底帽變換。
頂帽變換和底帽變換
灰度級影象 f 的頂帽變換(top-hat transformation)定義為f減去其開操作:
類似地,f 的底帽變換(bottom-hat transformation)定義為f的閉操作減去f:
這兩個變換的主要應用之一是,用一個結構元通過開操作或閉操作從一副影象中刪除物體,而不是擬合被刪除的物體。然後,差操作得到一副僅保留已刪除分量的影象。頂帽變換用於暗背景上的亮物體,而底帽變換則用於相反的情況。由於這一原因,當談到這兩個變換時,常常分別稱為白頂帽變換和黑底帽變換。它們一個重要用途是校正不均勻光照的影響。[1]
例項
下面,我們通過一個例項來說明此方法,對於圖1(a),可以看到光照明顯不均勻,左邊光照更強,直接進行otsu法全域性閾值得到圖1(b),可以看到左邊的硬幣分割出錯。
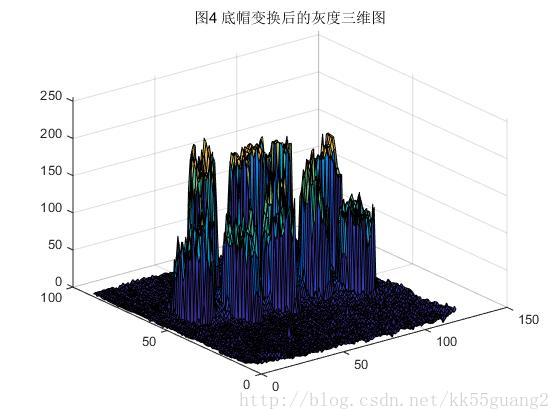
由於原圖是背景亮,前景暗,對原圖進行底帽變換以解決光照不均勻的問題,這裡先給出處理結果,如圖1(c)和(d),可以看到底帽變換後的影象刪除了大部分非均勻背景,最後閾值處理後,左邊的硬幣被分割出來,有少量殘缺,但是影響不大,後續可以通過形態學的其他處理將殘缺補齊。

圖1 處理影象
那麼為什麼底帽變換或頂帽變換可以達到上述效果呢,下面以底帽變換為例,通過影象的灰度三維圖來進行解釋。
底帽變換為f的閉操作減去f,閉運算可以幾何意義是讓球體緊貼在曲面的上表面滾動,此時球體任何部分所能達到的最低點即構成了閉運算
的曲面。[2]
圖2為原圖灰度三維圖,上方彎曲的走勢顯示了影象各部分光照不均勻造成的背景灰度不均現象,其中凹陷對應影象中灰度值比較小的區域,也就是影象中的硬幣。
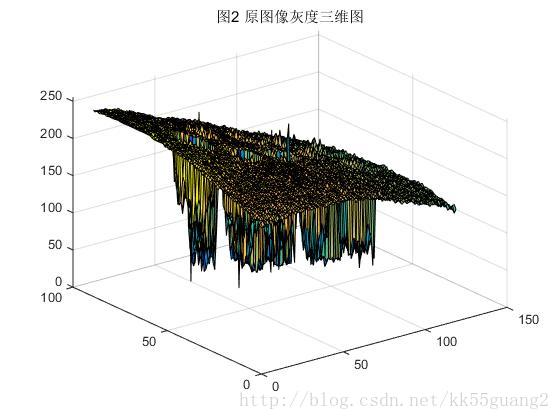
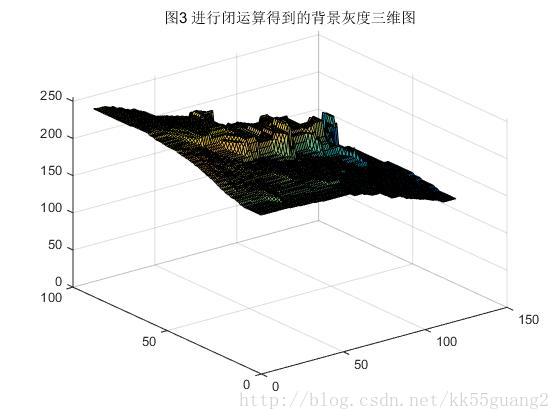
通過選取大於硬幣大小的合適結構元,可以看成一個球體在灰度曲面上滾動,球體下表面的軌跡構成閉運算的曲面,如圖3所示,原圖中的凹陷都被填上,可以近似代表不均勻的背景。閉運算完之後再減去原影象即可得到背景近似均勻的影象,如圖4所示,對應的灰度圖可以看圖1(c),可以看到不均勻的背景被大致去除,這將十分有助於後面的閾值分割。
參考文獻
[1]《數字影象處理》(第3版),岡薩雷斯著,阮秋琦譯,電子工業出版社,2013年;
[2]《數字影象處理與機器視覺——Visual C++與Matlab實現》,張錚,王豔平,薛桂香等編著,人民郵電出版社,2014年
