codeforces好題集合 (持續更新)
再次感到智商的不足,所以決意以後必須多刷cf了,cf不僅鍛鍊智商,還能鍛鍊程式碼能力,鍛鍊手速,是非常不錯的,以後要多做,就算現在被虐成翔,相信一年之後也會有很大的提高。讓我們 一起享受智商被碾壓 的快感把
首先是最近一場cf的div1的AB兩題
題意:給你三根木棒長度為a,b,c,然後給你長度 l 的木棒,讓你可以把a,b,c隨意加長,但是加長的總和不能超過l的方案數(可以不加長)
題解:我看到這題基本沒多少想法,就算有不敢說是對的,沒有很好的方法解決
那就開門見山把,用題解的方法,這題正著比較難,所以就先求出所有分棒子的情況,然後去掉裡面不能構成三角形的情況(orz)
所有分棒子的情況,就是個組合問題,假設有a,b,c分別增加了x,y,z,x+y+z=i<=l (0<=i<=l)
就是把i長度的棒子切成三段,切兩刀,(假設第一刀一定在第二刀的前面或者同一處)
長度i的棒子,一共有i+1處可以切,因為可以分給a長度0-i,所以有i+1刀
如果第一刀切0,第二刀也有i+1種
第一刀切1,第二刀就有i種切法
所以總的方法就是(i+1) +(i) + (i-1)+……+1=C(i+2,2);
0<=i<=l,所以所有分棒子的方法就是C(2,2)+C(3,2)+……C(l+2,2)
根據排列組合公式,C(2,2)=C(3,3),+C(3,2) =C(4,3),+C(4,2)=C(5,3)
所以C(2,2)+C(3,2)+……C(l+2,2)=C(l+3,3) 這是總的分棒子 的方法
然後就是求不能構成三角形的情況啦,我感覺這個考慮方法比較巧妙
先考慮把a增加之後的邊考慮成最長邊並且使三角形不成立,就是b+c=a+i
然後就是考慮從a+i,a+i+1……a+l,這些情況,當a+i,b,c構不成三角形的時候,要把剩下的l-i的長度分給b,c,並且使b‘+c’<=a+i
此時能夠分給b,c的長度為min(l-i,a+i-b-c)=x;然後將這段分給b,c的情況,就是C(x+2,2)
為什麼呢,同上,就是長度x的棒子,切兩刀,前兩段給b,c,最後一段扔掉好了
這樣就是最長邊是a所在的邊的不能構成三角形的情況
b,c同理
並且這樣考慮不會有重複,因為你定的最長邊就不一樣
程式碼十分簡短,這就是cf的魅力,我要 繼續努力,終有一天爭取能在div1立足,腦洞開之
/****************************************************************華麗的分割線***********************************************************************/
這題目沒有輸入,題意比較呵呵,我都沒理解,後來年神帶我過了之後感覺這題還是非常的好
題意:給你個2*1000的長方形,然後上面有個小偷,小偷每次可以往6個方向逃竄,左右,左上左下,右上右下,然後你是警察,你每次可以派兩個警察進行搜查,就是可以搜查兩個點,問你最小需要多少次,你肯定可以找到小偷
題解:剛看完題是不是很呵呵,所以我還練習的不夠,瞎找肯定是不可能的,所以肯定是有規律的,兩個警察必須在同一豎行,這樣可以把長方形的寬2都填滿,然後一格一格的搜尋,因為發現小偷每次是隻能左右的移動,如果你兩個搜尋點疊著,那麼上下都可以不考慮了,等於就是一個1*1000的長方形,裡面你用一個警察去搜索小偷,然後這要應該考慮格子的奇偶關係,如果小偷開頭在偶數,你也在偶數,那麼你從最後一格1000開始往前走,肯定能找到,如果小偷在奇數,你在偶數,那麼肯定最後會錯過,當你從1000搜到1的時候,小偷這會在偶數,下一步小偷在奇數,你應該也從奇數開始搜,就是999開始往前,所以一共最少1999次可以肯定找到
程式碼三行,就不貼了,這題目還是不錯的,我現在是閱讀理解能力和腦洞都不足啊還需努力
一天一場cf,健康生活五十年啊
/*********************************************************************************************************************************************************/
題意:給一個點,然後可以走紅色或者藍色的路,然後走到底之後,從根節點到葉子節點的路上面一共有n條藍色n條紅色邊,問最後樹裡有多少個點
題解:比如第i層,走了i條邊,所以在第n+1層的時候有兩個點只能走一種顏色了,然後在i>n的情況下,每次都有一些點只能走一個顏色,可以用組合數求出來,
就是2*C(i,i-n)個點只能走一種顏色,其中要用逆元求解一下組合數
/*********************************************************************************************************************************************************/ 題意:給你n個東西,每個東西有高度,然後類似於搭積木一樣,一次操作可以把最外圍的方塊都去掉(至於什麼是最外圍,就是他周圍至少有一邊沒有方塊),然後問你最少多少次操作可以把所有方塊都去掉 題解:一開始我想的是二分,但是二分之後不會判斷什麼時候已經被去掉了 看題解說的是做一次操作h[i]=min(h[i-1],h[i]-1,h[i+1]),類推操作k次就是h[i]=min(h[i-j]-(k-j),h[i+j]-(k-j)) 唉都提示到了這裡我居然都沒寫過,其實不需要用二分,應該考慮每個i,最少操作多少次能到0,然後求這些操作的最大值 然後考慮h[i]=min(left,right),left=h[i-j]-(k-j),left=0,k=h[i-j]+j,就是找i前面的h[i-j]+j最小的,換言之就是找h[t]+i-t;最小的,那麼只要設個值,每次記錄h[t]-t的最小值,然後每個i的時候+i更新一下就好了就是這個點的k,right也同理,就是從n開始往前遍歷,找h[t]+t的最小值,然後最後-i 然後就是邊界值的問題,h[0]=0,h[n+1]=0。。。。h[0]-0=0,h[n+1]+n+1=n+1,所以左邊從0開始算,右邊從n+1開始算 唉腦洞還是不行,思維能力也不如以前啊,最近成為了模版流,是時候走起一波cf了,提升一下腦洞 /********************************************************************************************************************************************************/ 題意:給你n個數,在其中選出一些數,能否被m整除 題解:這題一開始想的是,先全部模m,然後揹包一發,不過n是10的6次,m是10的3次,10^9的複雜度剛不住啊,然後就秒躺 其實我以前用過bitset優化揹包,經過實踐bitset是可以優化10^9次的揹包 就是每次輸入一個數模m之後得到x做位運算,先左移x位與自身取或,為了防止溢位再右移m位與自身取或,每次做完這些之後要把x為變成1,因為這是揹包,最後考慮0位是不是1就行了(為啥不是考慮m位,因為如果就輸入1個數,輸入的是0呢) 然而這肯定不是標準解法啊 其實這題可以用抽屜原理優化複雜度,n個數,構造n個 a1,a1+a2,a1+a2+a3,。。。a1+a2+。。。+an,這些數模m,得到n個餘數,如果這n個數中有數字模m得0的,那麼就找到了,如果都沒有0的,那麼最多有m-1種餘數,此時有n個餘數,只要n>m-1,那麼必定有兩個餘數相同,然後這兩個數字相減,得到的就是一些數的和,可以整除m,所以說n>=m的時候必定是YES,這樣就可以把n優化成10^3,揹包就變成了10^6,然後寫揹包的時候注意溢位什麼的就行了 /********************************************************************************************************************************************************/ 第一次做div2的最後題啊好激動啊,其實知識這題題意比較好理解,然後就試著想了一下,不過還是跪了 題意:給你n個點的座標,然後讓你求一條路徑,這條路徑包含n個點,每個點之間的距離是曼哈頓路徑,求出一條路徑的長度小於25*10^8 題解:我一開始以為這種題就是排個序,橫著搜一遍豎著搜一遍,但是這樣找到的肯定不是最優解,而且最優解的話估計要用dp,也許承受不起這個複雜度 看了題解才發現這是個構造題,唉我構造題基本不會,沒怎麼做過,水的一比 這題是要構造一個解,滿足條件,並不需要最優,首先座標範圍是0-10^6,題解很巧妙的把它豎著分成1000個10^3*10^6的長方形,然後每次走完一個長方形再走另一個 奇數個長方形從下往上走,偶數個長方形就從上往下走,只要排序y即可,這樣構造的最壞情況,就是1000個長方形走了10^6的y軸距離,x軸的話,在每個長方形裡走,用了1000*10^6,還有跨越長方形的花費2000*1000,最壞情況是2*10^9+2000000,完全滿足題目條件啊 從此好好練習cf,要有耐心看英文題,開動腦筋,鍛鍊思維 /***********************************************************************************************************************************************************/ 這題也是一個挺有難度的題,dp題(dp是必須要日積月累了) 題意:給你一個初始位置,還有n個區間位置,區間裡燈亮著,然後你現在可以關燈,你關閉一個區間的花費就是你現在的位置到這個區間的最小值,如果你在區間裡,那麼就是0花費,你還可以走到區間裡,這樣關燈就是0花費,但是走的距離就是花費 題解:這題是用dp解決,其實還是很難的,首先就是狀態的問題,首先考慮肯定是走到區間的左右端點或者隔空關燈也是在區間端點的位置才能使花費最小,然後就只有1W個點了,所以可以把座標離散化一下,這樣就5000次關燈,10000個點,可以用dp解決 當然這樣也許也開不下,所以就用滾動陣列dp[2][10005],這樣記錄前一次和這一次的狀態即可,這樣表示第i次站在j的位置,關掉第i個區間的燈的最小花費 然後轉移就可以從左邊或者右邊靠近j這個位置 首先從左邊靠近,先計算tmp2表示在j位置關燈的花費,然後tmp1記錄在j左邊的位置關掉i-1個區間之後走到j的位置的最小花費,然後dp[i][j]=tmp1+tmp2 從右邊靠近也是這樣的道理 最後列舉第n個區間在0-k個位置上的最小值 /********************************************************************************************************************************************************/ 題意:這題其實是個大水題,不過我太二逼了,導致居然過了這麼多人的題都做不出。題意是給你一個序列,如果這個數比他前面所有數字的總和大於等於,那麼他就是開心的,否則就是不開心,讓你重新更改順序,是開心的人最多 題解:排序,肯定的,然後如果碰到一個人不開心,那麼把他扔到最後也不會影響他是否開心,反而會讓後面開心的人更多,所以只要碰到不開心的就扔 這種題我居然都沒想清楚,還不敢寫,真是有夠水的,不過必須知恥而後勇,加油 /************************************************************************************************************************************************************/ 題意:求一個源點的最短路樹的權值,並且輸出是哪些邊 題解:30W的資料量,並且spfa不知道如何記錄邊,dijkstra可以很好的記錄邊,所以就用dij+heap優化,時間複雜度沒問題了,然後就是最短路樹,那麼不僅要在dis[v]>dis[u]+c的地方進隊,還要在dis[v]==dis[u]+c的地方,因為如果相等,這個u的dis肯定比前面更新v的dis更大,說明這個c更小,取得邊更小,同樣得到最短路,那麼最短路樹的權值也相應最小,邊的話可以用前向星,當前序號除以2來記錄 最後注意權值很大,會爆int,需要用LL ,在這裡交了兩發WA /************************************************************************************************************************************************************/ 題意:這題是歷史遺留問題了,以前一直沒有做,現在做了下,方法真是巧妙orz,服了,真心不錯,這題交給我們的思維方式,確實不一般 這題求一個序列的這個公式值,然後可以改變順序,使值最小 題解:這題確實一開始沒法上手,其實可以這樣發現,i-i+k-i+2k,這樣每隔k個 就可以把這些數都分在一組,然後要求這組的相鄰差值和最小,那麼就是max-min,所以就可以把一開始的序列排序,然後一組一組取,這樣就只要關注兩端點的差值 然後如何分組呢,可以看出來一共分成k組,可以分成n%k個長度為n/k+1的組(就是最後那些多出來的數,導致一些組的數字比其他組多一個) 還有一些就是k-n%k個長度為n/k的組,然後就可以用遞推了,dp[i][j]表示去了i個前一種組,j個後一種組的最優解 然後這會取的最後一個值就是a[i*(n/k+1)+j*(n/k)],max-min就是前面的減去某一組的長度 轉移if(i>=1) dp[i][j]=min(dp[i-1][j]+a[cnt]-a[cnt-l],dp[i][j]);if(j>=1) dp[i][j]=min(dp[i][j-1]+a[cnt]-a[cnt-l+1],dp[i][j]);/****************************************************************************************************************************************************************/ 題意:求sigma n mod i ,(1<=i<=m) 題解:這題感覺十分之難,光看肯定看不出,複製一發官方題解。
Let's transform the sum .
Note that the last sum can be accumulated to only valuemin(n, m),
because fori > nall the values will be equal
to0.
.
Note that the last sum can be accumulated to only valuemin(n, m),
because fori > nall the values will be equal
to0.
Note in the last sum either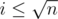 or
or .
Let's carefully accumulate both cases. The first sum can be simply calculated by iterating over all
.
Let's carefully accumulate both cases. The first sum can be simply calculated by iterating over all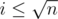 .
We will accumulate the second sum independently for all different values
.
We will accumulate the second sum independently for all different values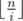 .
Firstly we should determine for which valuesiwe will have the value
.
Firstly we should determine for which valuesiwe will have the value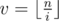 .
Easy to see that for the valuesifrom the interval
.
Easy to see that for the valuesifrom the interval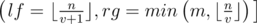 .
Also we can note that the sum of the second factors in
.
Also we can note that the sum of the second factors in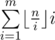 with
fixed first factor can be calculaed in constant time — it's simply a sum of arithmetic progression
with
fixed first factor can be calculaed in constant time — it's simply a sum of arithmetic progression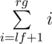 .
So we have solution with complexity
.
So we have solution with complexity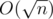 .
.
 ,然後就是分類討論i,因為後面這兩個東西的乘積肯定小於等於n,所以先考慮i<=根號n的時候,直接可以列舉算,然後考慮前面那個小於等於根號n的情況,假設它為v,然後可以發現i在一個範圍內,n/i都等於這個v,然後可以算出i的範圍
,然後就是分類討論i,因為後面這兩個東西的乘積肯定小於等於n,所以先考慮i<=根號n的時候,直接可以列舉算,然後考慮前面那個小於等於根號n的情況,假設它為v,然後可以發現i在一個範圍內,n/i都等於這個v,然後可以算出i的範圍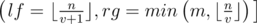 範圍是這個,左開右閉,然後就能根號n的複雜度內解決問題了
/******************************************************************************************************************************************************************************************/
題意:給你一個圖,然後每個點有a或者b或者c,然後每個字母和它相同的字母或者相鄰的連邊,a-a,a-b, b-b,b-a,b-c,c-c,c-b這樣,然後給你圖的邊,讓你求出這樣每個點的字母。
題解:我是太蠢了,以為是dfs就直接寫爆搜了,然後不知道哪裡寫錯了,還各種TLE,跪翻,其實做題應該靜心仔細想,我感覺我是那種靜不太下心來想的人,其實b可以和a,b,c三種連,所以度為n-1的點肯定為b,然後a的肯定都連在一起呢,所以直接搜一次把a的都搜出來,剩下的當作c,然後判斷是否可行,所以點和邊判一下就好了,以後要靜心想,cf不太考很煩的爆搜的
好好努力,never give up
/************************************************************************************************************************************************************************************/
題意:給你一個數字a,然後導致為ar,a+ar=n,給你n,讓你找符合條件的a;
題解:這題就是個思路題,但是比較麻煩,要考慮的有點多,開頭自己想的時候只想到首尾開始一起判,但是沒想好不同了怎麼處理
後來看了題解發現是,首尾開始判i和len-i-1,有幾種不同的情況:
1.要麼相同,就i++
2.要麼前面i比後面len-i-1大1,i位減1,然後給i+1位加10
3.要麼前面i比後面len-i-1大11,i位減1,給i+1位加10,然後他比後面第len-1-i位大10,轉入下面的判斷
4.要麼i比len-i-1位大10,那麼就是len-i-2要減1,給len-i-1加10,去掉這個進位,然後再判是否相同
每次判完都要回到第一步判,然後就能很清楚的搞定了,其中如果是奇數長度的話,就再判一下中間一位
但是這樣並不一定結束了,因為如果你兩個長為5的數相加,得到長度為6的數字,你用上面的判法是得不到正確結果的,所以還需要接下去的判斷
如果第一位為1,並且長度大於1,就把第一位的1給後一位加上10,然後變為長度減1的一個數,然後在用上面的方法判斷,如果還得不到的話就是不存在了
/**********************************************************************************************************************************************************************************/
題意:給你n個人,然後你可以抓他們,抓住他們每個人的概率是pi,然後猜他們是誰,如果n 個人都被抓到並且猜對了,遊戲結束,問你最小的遊戲回合數的期望是多少
題解:貪心,一開始都沒理解題意,搞了半天不明白,其實這題是這樣,你要求期望小,那麼小的回合數的概率應該大,然後有幾次應該是你選了某人,但是猜錯了他的名字,我不清楚有沒有別的做法, 題解上是考慮的猜了第i個人名字ki次,然後sum ki =t(t為遊戲回合數),然後sum t*prob(t)=期望
當n回合的時候,肯定是pi相乘,然後考慮第n+1回合,ai為抓住i的概率,bi為沒抓住i的概率,ci為所有人名字一共喊了i次並且遊戲能在i次以內結束的概率,然後考慮喊了i有ki次,然後喊i這麼多次,並且遊戲能結束的概率是ci=連乘(1-(1-a[j])^kj),喊了kj次j,並且每次都沒抓住j,然後1-這些,等於kj次裡面至少一次抓住j的概率,然後連乘,就是i回合裡面每個人都至少抓了一次,然後ci-ci-1的話就是正好i回合結束的概率了,然後現在就要考察第i回合應該喊誰能讓概率最大,如果是喊x,那麼就是乘上(1-b[x]*(1-a[x]))/(1-b[x]);
所以只要遍歷n找讓這個式子最大的x就行了,然後誤差要小於1e-6,看題解說至少30W次,所以遍歷30W回合就行了
/*********************************************************************************************************************************************************************************/
題意:給你一個序列,然後你可以把其中一段連續的去掉,花費是len*a,也可以把其中幾個數字+1或者-1,然後每個數字操作的花費是b,但是不能刪去整個數列,求最小花費能讓剩餘序列的gcd大於1的
題解:首先這題要觀察到因為不能全部去掉整個序列,而且去掉只能去一次,而且必須連續,所有左右兩個端點必有一個不會被去掉,然後直接把a1,a1+1,a1-1,an,an-1,an+1分解質因數,然後考察整個序列,和哪個因子的時候花費最小就行了(因為只要gcd大於1就行)
開兩個陣列,p1[i]表示從1-i的用+1,-1操作滿足因子為t的時候的花費,p2[i]表示從i-n用+1 -1操作滿足的花費,先處理出這些,然後用dp來處理連續的一段是刪除還是用+1 -1
ans=min(p2[i]+a*(i-1)+mv),p2[i]是說從i-n用+1 -1,前面用刪除,然後mv=min(p1[i]-a*i),就是維護i-1前面這些中這個值最小,然後1-j這一段不刪除,j+1-i-1刪除,這樣就算出了刪除的如果在中間或者從開頭刪的情況,但是還有從後面開始刪的情況沒考慮
ans=min(p1[i]+a*(n-i))這樣就是從後面刪的情況
我感覺這題主要要學會發現為啥題目給了不能全部刪去,還有就是刪除中間一段的這個dp操作,我dp太爛了,這種操作一直寫不好
/**************************************************************************************************************************************************************************************/
題意:給你一個n,告訴你有n種字母,然後告訴你每種字母有ai個,然後要你構成一個項鍊,然後剪開來能得到迴文串的最大方法
題解:因為剪開來是迴文串,所以如果奇數個數的珠子如果大於1的話,剪開來肯定不能得到迴文,然後如果能構成迴文,那最多有多少種方法呢,方法就是所有ai的gcd,很明顯吧,因為ai的話有ai個剪得地方,然後有n個ai,所以就是gcd
然後就是輸出了,因為奇數是比較特殊的,所以如果只有1種切法,那麼可以分成左右兩半,然後中間夾著一個奇數,所以可以先分成2*gcd段,構造一段,然後偶數就是除以2*gcd,裡面隨便放就行了,奇數是先減去gcd然後除以2*gcd,然後輸出時,先正著輸出,夾著個奇數的,然後倒著輸出,然後這樣迴圈gcd次,如果沒有奇數,中間就不加奇數
/***************************************************************************************************************************************************************************************/
題意:給你一個s串,括號,然後前面加個p串,後面加個q串,得到的p+s+q,裡面(和)數量相同,然後對於每個字首,(的數量都大於等於 )
題解:先對後面的q串進行dp預處理,dp[i][j]表示還有i個(和j個)的時候的方法
然後對前面p串進行dp,dp[i][j]=dp[i+1][j]+dp[i][j+1]+(q[a][b]),後面加的這個是當i-j滿足大於等於s串裡面)減去(的最大值
/**************************************************************************************************************************************************************************************/
題意:給你n個蛋糕的尺寸,然後j蛋糕可以放在i蛋糕上面,滿足j>i,Vj>Vi,問你得到的最大體積是多少
題解:先給蛋糕體積排序,體積相同就大的序號在前,然後開個線段樹存當前區間最大體積是多少,然後就線段樹搞搞就好了
/************************************************************************************************************************************************************************************/
題意:給你n個數字,讓你分成若干組,每組的不平衡值為組裡面最大的數字減去最小的數字,一個數也可以單獨為一組,然後這組的不平衡值為0,問你所有組不平衡值小於等於k的分法有多少種
題意:這題好難啊,首先應該想到是dp,就是對於每一個數字,他應該是一組的開頭,或者中間,或者結尾,中間的話可以算是自成一組然後放在中間或者外面
然後我就考慮n^2*k複雜度的dp,但是每次考慮這個點是結尾的時候再去算不平衡值,然後統計個數很複雜啊,怎麼搞都搞不出來
看了廁神的方法,首先這題要設當前有j個組,然後第i個放進去,是放j個組其中,還是自成一組的開頭,還是關閉一個組,有三種轉移,於此同時,需要在每次轉移的時候都計算不平衡度,這就需要用到提前消費的思想,比如這會有j個組,然後放a[i],就要把a[i]-a[i-1]的不平衡度給每個組都加上,然後下一次放a[i+1]的時候,就能消掉。
雖然我不是很確定這樣提前消費會不會爆總的不平衡度上限,但是這樣是可以過題的otz
/************************************************************************************************************************************************************************************/
題意:給你n個數字,然後讓你取一些構成一個集合,要求是集合裡的平均值減去中位數要儘可能大,問你取多少個,和每個分別是什麼
題解:首先這題看見了也是無從下手,需要發現一個性質,就是集合裡肯定要奇數個,為什麼呢,其實我也不是很明白,就這麼想吧,如果是偶數個,去掉比中位數大的那個數,中位數下降比平均數多。。。
Let’s fix the median at xi (in the sorted list), and set the size of the set to 2j + 1. We’d like to maximize the mean, so we can greedily choose the largest j elements below the median and the largest j elements above the median: xi - j, ..., xi - 1
and xn - j + 1, ..., xn.
sorted!!!!!!!!!!!!!!!!!!!!千萬不要忘記排序,因為在兩邊取的時候應該是使用三分(因為兩邊取的時候肯定是有可能先遞增後減,或者是先減後增這樣的,所以需要先排序,不然就不能確定只有一個極值點了!!!!因為這個錯了好久)
為什麼呢 sum[x]-sum[x-r-1]+sum[n]-sum[n-r],如果不排序,你能確定這個值在長度遞增的時候是遞增的麼(不能把,我真是chun)
然後就是三分了,三分的話是要寫自己習慣的寫法,我開頭寫對的,但是因為沒排序,導致一直wa,後來抄了一半別人的三分,還是錯otz
如果是整點的三分以後就用這個寫法了orz
/************************************************************************************************************************************************************************************/
題意:給你一個矩陣,然後按照矩陣裡原來的大小順序,設計一個新的矩陣,讓矩陣裡最大的值最小
題解:大小關係的話就是拓撲關係,所以類似拓撲排序肯定是要的,但是裡面有些值大小是相同的,如果建立拓撲關係的話100W點,最好就相鄰的建一條邊還能承受,如果有相同的,就很煩了,所以首先需要並查集,把行列裡相同的都並起來,然後建邊,拓撲排序一下,最後輸出就OK了,並不是很難,但是沒想到並查集我還是太弱了啊
/************************************************************************************************************************************************************************************/
題意:給你兩個字串,但是這個字串的話,十分之長,有連著l個同一個字元,然後l有100W,求第二個字串在第一個裡面出現多少次啊
題解:字串匹配問題嘛,肯定是KMP啦,就是個結構體的KMP,然後先需要把相鄰一樣的字元的l給合併了,然後kmp呢,不太好k,因為b串兩端的字元在a串裡匹配可能比a串裡那一塊少,但是也是能匹配的,所以就需要先把b串左右兩端減掉(如果長度是1和2就直接遍歷判斷吧),然後拿中間的去a串裡做kmp,找到的時候,就判一下左右兩端,是不是a串裡兩端的l都大於等於b串的兩端,就可以了
這題我wa的一個地方就是kmp b串的長度是len,就必須是len,我自以為規定他長度len,但是用的串其實長度是len+1,然後wa
一定要另外開個陣列搞
/**************************************************************************************************************************************************************************************/
題意:讓你求一個能被m整除的,偶數位為d的數字的個數,在[a,b]之間
題解:數位dp咯,但是這題有個坑點就是前導0,需要記錄的幾個狀態也就是剩餘長度,當前是奇數偶數位,餘數,是否是邊界,是否有前導0
然後我跪了好久是因為,給dp賦值和返回的時候,應該要先判斷當前前面不是前導0,我沒判斷,跪了好久,後來好不容易才發現了枸蒻了
/************************************************************************************************************************************************************************************/
題意:最長串lcm小於等於k
題解:唉這種題我居然當時都不會做,因為m只有10^6,所以可以直接列舉每個數的倍數,用陣列標記,然後找到下標最小的值最大的就行了
先排序離散化,所以複雜度是n+n/2+n/4+...=2n
唉水題啊我居然都秀逗了
最近經常犯水題反而想複雜不會做的毛病,是不是得治啊!!!
/*****************************************************************************************************************************************************************************************/
題意:給你一棵樹,然後給你m個限制,是a和b之間不能有邊!然後告訴你點1正好連著k個邊,問你能還原樹麼
題解:點1的限制先不考慮,可以先考慮是否能構成樹,就是連通,然後連通也不太好判,因為有很多的邊啊,所以你需要開個set記錄不能有的邊,然後開個set記錄還沒找的點,然後從1開始在還沒找的點裡面找可以連的,然後dfs下去,刪刪刪,然後看能否連通
連通了之後就是判能和1相連的是否大於等於k,還有就是k是否大於等於剩下的點最少能夠構成的連通塊,為什麼呢,因為首先一些點是隻能和1相連,然後我一開始以為剩下的點都能連成一塊,然後一直跪,後來發現其實不是,比如a,b連起來和1相連,c不是隻能和1相連的點,d也是如此,然後c,d都不能和a,b相連,只能c,d之間互相相連,所以需要求最少的連通塊,然後k大於等於它,這個計算可以在搜的時候一起記錄
範圍是這個,左開右閉,然後就能根號n的複雜度內解決問題了
/******************************************************************************************************************************************************************************************/
題意:給你一個圖,然後每個點有a或者b或者c,然後每個字母和它相同的字母或者相鄰的連邊,a-a,a-b, b-b,b-a,b-c,c-c,c-b這樣,然後給你圖的邊,讓你求出這樣每個點的字母。
題解:我是太蠢了,以為是dfs就直接寫爆搜了,然後不知道哪裡寫錯了,還各種TLE,跪翻,其實做題應該靜心仔細想,我感覺我是那種靜不太下心來想的人,其實b可以和a,b,c三種連,所以度為n-1的點肯定為b,然後a的肯定都連在一起呢,所以直接搜一次把a的都搜出來,剩下的當作c,然後判斷是否可行,所以點和邊判一下就好了,以後要靜心想,cf不太考很煩的爆搜的
好好努力,never give up
/************************************************************************************************************************************************************************************/
題意:給你一個數字a,然後導致為ar,a+ar=n,給你n,讓你找符合條件的a;
題解:這題就是個思路題,但是比較麻煩,要考慮的有點多,開頭自己想的時候只想到首尾開始一起判,但是沒想好不同了怎麼處理
後來看了題解發現是,首尾開始判i和len-i-1,有幾種不同的情況:
1.要麼相同,就i++
2.要麼前面i比後面len-i-1大1,i位減1,然後給i+1位加10
3.要麼前面i比後面len-i-1大11,i位減1,給i+1位加10,然後他比後面第len-1-i位大10,轉入下面的判斷
4.要麼i比len-i-1位大10,那麼就是len-i-2要減1,給len-i-1加10,去掉這個進位,然後再判是否相同
每次判完都要回到第一步判,然後就能很清楚的搞定了,其中如果是奇數長度的話,就再判一下中間一位
但是這樣並不一定結束了,因為如果你兩個長為5的數相加,得到長度為6的數字,你用上面的判法是得不到正確結果的,所以還需要接下去的判斷
如果第一位為1,並且長度大於1,就把第一位的1給後一位加上10,然後變為長度減1的一個數,然後在用上面的方法判斷,如果還得不到的話就是不存在了
/**********************************************************************************************************************************************************************************/
題意:給你n個人,然後你可以抓他們,抓住他們每個人的概率是pi,然後猜他們是誰,如果n 個人都被抓到並且猜對了,遊戲結束,問你最小的遊戲回合數的期望是多少
題解:貪心,一開始都沒理解題意,搞了半天不明白,其實這題是這樣,你要求期望小,那麼小的回合數的概率應該大,然後有幾次應該是你選了某人,但是猜錯了他的名字,我不清楚有沒有別的做法, 題解上是考慮的猜了第i個人名字ki次,然後sum ki =t(t為遊戲回合數),然後sum t*prob(t)=期望
當n回合的時候,肯定是pi相乘,然後考慮第n+1回合,ai為抓住i的概率,bi為沒抓住i的概率,ci為所有人名字一共喊了i次並且遊戲能在i次以內結束的概率,然後考慮喊了i有ki次,然後喊i這麼多次,並且遊戲能結束的概率是ci=連乘(1-(1-a[j])^kj),喊了kj次j,並且每次都沒抓住j,然後1-這些,等於kj次裡面至少一次抓住j的概率,然後連乘,就是i回合裡面每個人都至少抓了一次,然後ci-ci-1的話就是正好i回合結束的概率了,然後現在就要考察第i回合應該喊誰能讓概率最大,如果是喊x,那麼就是乘上(1-b[x]*(1-a[x]))/(1-b[x]);
所以只要遍歷n找讓這個式子最大的x就行了,然後誤差要小於1e-6,看題解說至少30W次,所以遍歷30W回合就行了
/*********************************************************************************************************************************************************************************/
題意:給你一個序列,然後你可以把其中一段連續的去掉,花費是len*a,也可以把其中幾個數字+1或者-1,然後每個數字操作的花費是b,但是不能刪去整個數列,求最小花費能讓剩餘序列的gcd大於1的
題解:首先這題要觀察到因為不能全部去掉整個序列,而且去掉只能去一次,而且必須連續,所有左右兩個端點必有一個不會被去掉,然後直接把a1,a1+1,a1-1,an,an-1,an+1分解質因數,然後考察整個序列,和哪個因子的時候花費最小就行了(因為只要gcd大於1就行)
開兩個陣列,p1[i]表示從1-i的用+1,-1操作滿足因子為t的時候的花費,p2[i]表示從i-n用+1 -1操作滿足的花費,先處理出這些,然後用dp來處理連續的一段是刪除還是用+1 -1
ans=min(p2[i]+a*(i-1)+mv),p2[i]是說從i-n用+1 -1,前面用刪除,然後mv=min(p1[i]-a*i),就是維護i-1前面這些中這個值最小,然後1-j這一段不刪除,j+1-i-1刪除,這樣就算出了刪除的如果在中間或者從開頭刪的情況,但是還有從後面開始刪的情況沒考慮
ans=min(p1[i]+a*(n-i))這樣就是從後面刪的情況
我感覺這題主要要學會發現為啥題目給了不能全部刪去,還有就是刪除中間一段的這個dp操作,我dp太爛了,這種操作一直寫不好
/**************************************************************************************************************************************************************************************/
題意:給你一個n,告訴你有n種字母,然後告訴你每種字母有ai個,然後要你構成一個項鍊,然後剪開來能得到迴文串的最大方法
題解:因為剪開來是迴文串,所以如果奇數個數的珠子如果大於1的話,剪開來肯定不能得到迴文,然後如果能構成迴文,那最多有多少種方法呢,方法就是所有ai的gcd,很明顯吧,因為ai的話有ai個剪得地方,然後有n個ai,所以就是gcd
然後就是輸出了,因為奇數是比較特殊的,所以如果只有1種切法,那麼可以分成左右兩半,然後中間夾著一個奇數,所以可以先分成2*gcd段,構造一段,然後偶數就是除以2*gcd,裡面隨便放就行了,奇數是先減去gcd然後除以2*gcd,然後輸出時,先正著輸出,夾著個奇數的,然後倒著輸出,然後這樣迴圈gcd次,如果沒有奇數,中間就不加奇數
/***************************************************************************************************************************************************************************************/
題意:給你一個s串,括號,然後前面加個p串,後面加個q串,得到的p+s+q,裡面(和)數量相同,然後對於每個字首,(的數量都大於等於 )
題解:先對後面的q串進行dp預處理,dp[i][j]表示還有i個(和j個)的時候的方法
然後對前面p串進行dp,dp[i][j]=dp[i+1][j]+dp[i][j+1]+(q[a][b]),後面加的這個是當i-j滿足大於等於s串裡面)減去(的最大值
/**************************************************************************************************************************************************************************************/
題意:給你n個蛋糕的尺寸,然後j蛋糕可以放在i蛋糕上面,滿足j>i,Vj>Vi,問你得到的最大體積是多少
題解:先給蛋糕體積排序,體積相同就大的序號在前,然後開個線段樹存當前區間最大體積是多少,然後就線段樹搞搞就好了
/************************************************************************************************************************************************************************************/
題意:給你n個數字,讓你分成若干組,每組的不平衡值為組裡面最大的數字減去最小的數字,一個數也可以單獨為一組,然後這組的不平衡值為0,問你所有組不平衡值小於等於k的分法有多少種
題意:這題好難啊,首先應該想到是dp,就是對於每一個數字,他應該是一組的開頭,或者中間,或者結尾,中間的話可以算是自成一組然後放在中間或者外面
然後我就考慮n^2*k複雜度的dp,但是每次考慮這個點是結尾的時候再去算不平衡值,然後統計個數很複雜啊,怎麼搞都搞不出來
看了廁神的方法,首先這題要設當前有j個組,然後第i個放進去,是放j個組其中,還是自成一組的開頭,還是關閉一個組,有三種轉移,於此同時,需要在每次轉移的時候都計算不平衡度,這就需要用到提前消費的思想,比如這會有j個組,然後放a[i],就要把a[i]-a[i-1]的不平衡度給每個組都加上,然後下一次放a[i+1]的時候,就能消掉。
雖然我不是很確定這樣提前消費會不會爆總的不平衡度上限,但是這樣是可以過題的otz
/************************************************************************************************************************************************************************************/
題意:給你n個數字,然後讓你取一些構成一個集合,要求是集合裡的平均值減去中位數要儘可能大,問你取多少個,和每個分別是什麼
題解:首先這題看見了也是無從下手,需要發現一個性質,就是集合裡肯定要奇數個,為什麼呢,其實我也不是很明白,就這麼想吧,如果是偶數個,去掉比中位數大的那個數,中位數下降比平均數多。。。
Let’s fix the median at xi (in the sorted list), and set the size of the set to 2j + 1. We’d like to maximize the mean, so we can greedily choose the largest j elements below the median and the largest j elements above the median: xi - j, ..., xi - 1
and xn - j + 1, ..., xn.
sorted!!!!!!!!!!!!!!!!!!!!千萬不要忘記排序,因為在兩邊取的時候應該是使用三分(因為兩邊取的時候肯定是有可能先遞增後減,或者是先減後增這樣的,所以需要先排序,不然就不能確定只有一個極值點了!!!!因為這個錯了好久)
為什麼呢 sum[x]-sum[x-r-1]+sum[n]-sum[n-r],如果不排序,你能確定這個值在長度遞增的時候是遞增的麼(不能把,我真是chun)
然後就是三分了,三分的話是要寫自己習慣的寫法,我開頭寫對的,但是因為沒排序,導致一直wa,後來抄了一半別人的三分,還是錯otz
如果是整點的三分以後就用這個寫法了orz
/************************************************************************************************************************************************************************************/
題意:給你一個矩陣,然後按照矩陣裡原來的大小順序,設計一個新的矩陣,讓矩陣裡最大的值最小
題解:大小關係的話就是拓撲關係,所以類似拓撲排序肯定是要的,但是裡面有些值大小是相同的,如果建立拓撲關係的話100W點,最好就相鄰的建一條邊還能承受,如果有相同的,就很煩了,所以首先需要並查集,把行列裡相同的都並起來,然後建邊,拓撲排序一下,最後輸出就OK了,並不是很難,但是沒想到並查集我還是太弱了啊
/************************************************************************************************************************************************************************************/
題意:給你兩個字串,但是這個字串的話,十分之長,有連著l個同一個字元,然後l有100W,求第二個字串在第一個裡面出現多少次啊
題解:字串匹配問題嘛,肯定是KMP啦,就是個結構體的KMP,然後先需要把相鄰一樣的字元的l給合併了,然後kmp呢,不太好k,因為b串兩端的字元在a串裡匹配可能比a串裡那一塊少,但是也是能匹配的,所以就需要先把b串左右兩端減掉(如果長度是1和2就直接遍歷判斷吧),然後拿中間的去a串裡做kmp,找到的時候,就判一下左右兩端,是不是a串裡兩端的l都大於等於b串的兩端,就可以了
這題我wa的一個地方就是kmp b串的長度是len,就必須是len,我自以為規定他長度len,但是用的串其實長度是len+1,然後wa
一定要另外開個陣列搞
/**************************************************************************************************************************************************************************************/
題意:讓你求一個能被m整除的,偶數位為d的數字的個數,在[a,b]之間
題解:數位dp咯,但是這題有個坑點就是前導0,需要記錄的幾個狀態也就是剩餘長度,當前是奇數偶數位,餘數,是否是邊界,是否有前導0
然後我跪了好久是因為,給dp賦值和返回的時候,應該要先判斷當前前面不是前導0,我沒判斷,跪了好久,後來好不容易才發現了枸蒻了
/************************************************************************************************************************************************************************************/
題意:最長串lcm小於等於k
題解:唉這種題我居然當時都不會做,因為m只有10^6,所以可以直接列舉每個數的倍數,用陣列標記,然後找到下標最小的值最大的就行了
先排序離散化,所以複雜度是n+n/2+n/4+...=2n
唉水題啊我居然都秀逗了
最近經常犯水題反而想複雜不會做的毛病,是不是得治啊!!!
/*****************************************************************************************************************************************************************************************/
題意:給你一棵樹,然後給你m個限制,是a和b之間不能有邊!然後告訴你點1正好連著k個邊,問你能還原樹麼
題解:點1的限制先不考慮,可以先考慮是否能構成樹,就是連通,然後連通也不太好判,因為有很多的邊啊,所以你需要開個set記錄不能有的邊,然後開個set記錄還沒找的點,然後從1開始在還沒找的點裡面找可以連的,然後dfs下去,刪刪刪,然後看能否連通
連通了之後就是判能和1相連的是否大於等於k,還有就是k是否大於等於剩下的點最少能夠構成的連通塊,為什麼呢,因為首先一些點是隻能和1相連,然後我一開始以為剩下的點都能連成一塊,然後一直跪,後來發現其實不是,比如a,b連起來和1相連,c不是隻能和1相連的點,d也是如此,然後c,d都不能和a,b相連,只能c,d之間互相相連,所以需要求最少的連通塊,然後k大於等於它,這個計算可以在搜的時候一起記錄
