個人非常喜歡做DP題，因為DP題有著特殊的數學美感持續不斷吸引著我，不過最近因為事情繁忙，故好長時間沒有刷DP題了，現在空下來，是時候重操舊業了，就從Codeforce上的題入手，至於為什麼選這上面的題，因為目前DP題的走向趨向於狀態方程極度隱蔽化！！！ 而Codeforce上的題向來以巧妙著稱，DP題就更是妙上加妙，所以感覺刷這DP的題能讓人更上時代。

467C  George and Job

題目描述：

大致思路：

dp[i][j]代表前i個數中拿了j次m個數的最優情況，dp[i][j]=max(dp[i][j],dp[i-1][j-1],dp[i-m][j-1]+sum(i)-sum(i-m)); 5000*5000從空間上來說浪費太多，故用滾動陣列更好，細節自己處理一下。

參考程式碼：

466D Increase Sequence

題目描述：

大致思路：

dp[i][j]表示前i個數中還留有j個右開區間時的最優情況，dp[n][0]就是最終答案，然後考慮到i到i+1的情況，當且僅當i的右開區間等於h-a[i+1]或h-a[i+1]-1時有解，分類情況討論一下，即可得出狀態轉移方程。

參考程式碼：

463D Gargari and Permutations

題目描述：

大致思路：

神奇的DP思想，解題關鍵在於每個序列的數僅有1-n，dp[i]代表第一個序列中的前i個數在其他序列中的最長公共序列，然後對每個序列記錄數字1-n出現的位置，i到i+1的時候，判斷其他序列中a[1][1..i]這些數字中有多少數字的位置剛好也在本序列的a[1][i+1]這個數字位置之前，至於這些之前數字的排列所構成的最有情況，dp[i]已經算過了，所以可以直接用。

參考程式碼：

461B Appleman and Tree

題目描述：

大致思路：

樹形DP！每個點維護兩個值，一個值dp[root][0]是這個點不和黑相連，其餘子樹保證唯一黑點的切割情況，另一個值dp[root][1]是這個點開始的子樹的切割情況。剛開始時，黑點是0和1，然後白點是1和0；狀態轉移的時候，碰到child開始的子樹沒有黑點的child，直接跳過，有黑點情況的，          

dp[root][1]=dp[root][0]*dp[child][1]%mod+dp[root][1]*(dp[child][0]+dp[child][1])%mod;

dp[root][0]=dp[root][0]*(dp[child][0]+dp[child][1])%mod;

參考程式碼：

459E Pashmak and Graph

大致思路：

神奇的在有向圖上的DP，不過無後效性很明確，因為只有小邊能夠更新大邊，開始先根據邊權排序，也可以用vector，邊權較小。然後我的方法是每個點維護三個值，pr,v1,v2,pr代表這個點最新接進來的權值，v1代表pr權值接進來的以這個點為終點的最長不下降道路序列長度，v2代表小於這個權值接進來的最長不下降道路序列長度。為什麼這麼做原因很簡單，因為同樣邊權是不能更新同邊權的。若新邊權值大於pr，則v1，v2結合，若一樣，就通過v2來更新。

參考程式碼：

476E Dreamoon and Strings

大致思路：DP一般先貪心，形成一個P，我們一定是通過減少最少的步數使其形成，所以先預處理出S中每一個字元，若這個字元等於P最後一個字元，就記錄下能和它形成P的最近的一個P的第一個字元，若無法形成或者非P的最後一個字元，就記為-1，幾個例子：

axbaxxbab 預處理的結果為-1 -1 0 -1 -1 -1 3 -1 7

然後DP[i][j]為前i個取j個的最大個數，對於每個DP[i][j]都有     dp[j][i]=max(dp[j][i],max(dp[j-1][i],dp[j-1][i-1]));

然後若這個字元預處理的結果非-1，即它能通過減去特定字元多形成一組P，那麼這個狀態就可以通過dp[j][i]=max(dp[j][i],dp[pre[j-1]][t2]+1);這樣推得，t2為除了形成這一段P需要減去的t1之外，共減去i個情況下還需要減去的個數。

479E Riding in a Lift

大致思路：還算是簡單的DP，但是比賽中我第二題搞了太長時間導致沒時間搞這題，總的來說我還是太菜了。方法就是n^2,sum[i]為dp[1-i][j-1]的和，dp[i][j]=sum[i-1]+sum[fun1(i,b)]-sum[i]，fun1函式是個簡單的判斷，即判斷最遠能夠跳到i的樓層，這樣做開始得處理下a,b，如果a>b，那a=n-a+1,b=n-b+1；

478D Red-Green Towers

大致思路：略帶暴力的一道DP，題目中明確說明對於r+g，求達到最高高度情況下的種數，200000*2是四十萬，高度最高920，可以發現答案就是在可行前提下，不同數量的，紅色磚塊的可擺放的方案之和。即01揹包，雖然理論複雜度有10^8，但是題目給了兩秒，而且01揹包也有優化可以使複雜度/2，不會超時的，算完揹包就等於得到了h高度下，不同數量的，紅色磚塊的可擺放方案，把可行解找出來求和就可以了。mod那裡細節要處理好，不然可能會被卡常數。

486D Valid Sets

大致思路：這道DP題做出的關鍵在於找準切入點，而找準切入點的技巧是把段化點，每個符合條件的子串都擁有一個最小值，對應樹上的每個節點值，所以這題的做法就是，列舉根節點，只計算節點值等於根節點值或者在根節點值+d範圍以內的兒子節點有了這個大前提，就可以發現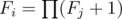,其中i為根節點，j為符合條件的兒子節點。

489F Special Matrices

大致思路：記憶化搜尋，狀態用列上1的個數和0的個數表示出來，最終結果一定是0個列上1和0個列上0，即全部為2.那麼就可以逆推了，開始時，只有給出的狀態，dp記為1，其餘全部為-1，表示還未計算過，對於給定的on（列上1的個數）和ze（列上0的個數），有三種方法推到它，一個是之前情況on中選兩個，由dp[on+2][ze]推得，一個是之前情況on中選一個，ze中選一個，由dp[on][ze+1]推得，因為此時ze減少一個的同時，on也加了一個，on又得減少一個，故得此。第三種情況是之前情況ze中選兩個，由dp[on][ze+2]推得，具體細節自己處理一下。

487B Strip

大致思路：資料結構+二分查詢+DP思想，做出這題得靠DP的思想，設f[i]為1---i這一段的最小劃分，f[j]可以由1---(j-1)這一段上的f[i]轉移過來，只要判斷i---j是否能構成新的一段即可，這可以用ST演算法O（1）（構造需要nlog(n)）的時間出來，判斷一下最大值和最小值是否符合就可以。但是n*n的時間複雜度顯然是不夠看的，所以要用二分查詢來加速，變成nlog(n)，仔細思考後會發現，因為有l的限制，所以其實f[j]只能由1---(j-l-1)這一段中的f[i]轉移過來，並且這一段中的f[i]是單調遞增的，所以二分這一段就可以了。

508E Arthur and Brackets

大致思路：DP一般先貪心，對於這道題，每個左括號要選擇最靠近自己左範圍的奇數距離，偶數距離是不可能的。為什麼這樣，你可以這樣想，如果全是1顯然滿足，然後如果有一個左括號不得不選x，那就意味著它的前一個左括號就必須選擇1或者大於x的距離了，x越大越不利。有了這個貪心的前提下，就是狀態轉移了，fa[i]表示該距離可行，每個左括號哪些距離可行僅由自己後面的左括號選擇的距離所決定，並且注意如果i+1括號選擇的距離為3，意味著i+2左括號被i+1左括號所利用，就不能通過它來更新i了。具體細節自己處理好。

510D Fox And Jumping

大致思路：很巧妙的一道狀壓DP，要是以為是揹包的話，你就走遠了。

                  先貪心一下吧，想要每個點都能走到，那幾個數字湊來湊去一定能得到1，這裡有個定理，當且僅當幾個數最大公約數為1的時候能湊出1.所以這題就變成了素因數的問題，10^9的範圍，素因數最多有9個，設dp[i][j]為選了魔法i,狀態為j時的最優值。狀態j為選了自己能夠得到的最大公約數，這隻跟自己的素因數有關係，而且注意最大公約數為4這種的沒有必要考慮，因為在計算除1之外的最大公約數時素因數才最重要，4相當於2。所以這個狀態最多為2^9=512，即9個素因數選擇了哪些。狀態出來了，轉移方程也就不難了，dp[i][j]=min(dp[i][j],dp[j][k]+c[i]);其中j=gcd(a[i],fun(k));fun(k)為j魔法k狀態對應的最大公約數。最後比較所有魔法的0狀態，即得到1的最大公約數的值。具體細節自己處理一下。

417D Cunning Gena

大致思路：戰術組合DP，m只有20，故可以狀態壓縮。但是狀態有1000000個，100個人不可能輪番把所有狀態都判一遍，所以要用vector把更新的狀態儲存下來，初始只有0.還有最關鍵一個問題，k的處理，其實也簡單。不用多增加一圍，只要把人根據k從小到大排序，這樣當出現問題全部解決的時候的這個k是最大的，只要這個時候計算k*b就行了。細節自己處理一下。

580D Kefa and Dishes

大致思路：2015.10.02日 這時我應該已經保研成功了，好久沒有暢快淋漓地做這種狀態壓縮DP了。這道題，要注意對於一個序列來說，向前繼續吃和向後繼續吃是統一的。所以只要計算一直向前吃就好了，狀態為dp[n][2^n]表示以n為開頭，吃了哪些東西的狀態。狀態轉移方程也很容易，即

dp[j][f4]=max(dp[j][f4],dp[i][f2]+f[j][i]+a[j]),f4表示吃了j之後的新狀態，f2表示未吃j之前的狀態，f[j][i]表示向前吃j。複雜度O（(2^n)*n*n）；