2. 程式人生 > >KMP匹配詳細講解+next陣列真正理解

KMP匹配詳細講解+next陣列真正理解

阿新 • • 發佈：2018-12-24
之前轉載過一篇kuangbin大佬的kmp模板，只會用，但是不清楚原理現在看了某大佬的文章，發現講解的非常精彩，但是有一點不足就是沒講清楚KMP時間複雜度問題，但是自己的語言組織能力以及理解能力也不是很好，所以就直接copyt過來了。希望_july_v博主不介意。http://www.cnblogs.com/kuangbin/archive/2012/08/14/2638803.htmlhttps://blog.csdn.net/v_july_v/article/details/7041827首先說明：KMP是解決一個文字串和一個目標串的匹配問題的。那麼假設目標串有很多個呢？是不是可以對於每一個目標串做一次KMP？？？這樣的話時間複雜度不就很高了，先TLE再說，對於這種多模匹配就需要用到ac自動機了，實際上kmp是ac自動機的退化版，至於什麼是ac自動機？那就不是本文範疇了，現在已經清楚了KMP作用，接下來看看一些東西然後聽july_v大佬講解吧！關於next複雜度問題：
假設模式串的長度為m，而next陣列是這樣對模式串進行處理的：對每個index i，都找next[i - 1]或者next[next[i -1]]去判斷下標 i 這個位置的數字應該是多少，所以總體就是一個下標“一次”運算，總共有m個，所以算next的時間複雜度是O(m)。整體複雜度如果從字串S（長度為n）中匹配字串T（長度為m）
要先對T進行遍歷，求一個next陣列複雜度為O(m)
根據next陣列匹配的時候，
當出現 S[i] != T[j]時，下一次的比較應該是S[i]和T [next[j]]進行比較，不需要回溯,複雜度為O（n）
因此，總的KMP時間複雜度為O( n+m )
/* 
時間複雜度：如果文字串的長度為n，模式串的長度為m，那麼匹配過程的時間複雜度為O(n)，算上計算next的O(m)時間，KMP的整體時間複雜度為O(m + n)。 

演算法說明： 
1、先通過目標串（ptr）計算出對應的首尾最長前後綴長度（Next1[]）對應的值 
2、再通過計算出的（Next1[]）“智慧”處理目標串在主串中的匹配過程 
*/ 
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+5;
int Next1[maxn];
char str[maxn],ptr[maxn];
void GetNext(int len)
{
Next1[0]=-1;//-1表示不存在相同的最大字首和最大字尾
int k=-1;
int j=0;
while(j<len-1)
{
if(k==-1||ptr[j]==ptr[k])//ptr[j]表示的為目標串的字尾，ptr[k]表示目標串字首
{
j++;
k++;
if(ptr[j]!=ptr[k]) Next1[j]=k;//當前字首和字尾不相同，將最長字首和最長字尾相同長度給Next1[]
else Next1[j]=Next1[k];//這相當於一個遞推的優化
}
else k=Next1[k];//下一個不相等就會向前回溯， 
}
}
int kmp_Search(int len1,int len2)
{
int j=0;
int i=0;
GetNext(len2);
while(i<len1&&j<len2)
{
if(j==-1||str[i]==ptr[j])
{
j++;
i++;
}
else j=Next1[j];//向前回溯，相當於移動目標串，移動的長度=當前匹配的長度-最長字首字尾相同的長度，程式碼表示為j-next[j]
}
if(j==len2) return i-j;//返回首次出現位置
return -1;//匹配不成功
}
int kmp_Count(int len1,int len2)
{
int j=0;
int i=0;
int cnt=0;
GetNext(len2);
while(i<len1)
{
if(j==-1||str[i]==ptr[j])
{
j++;
i++;
}
else j=Next1[j];
if(j==len2) cnt++;
}
return cnt;
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
getchar();//使得gets函式能夠接受帶空格的字串
gets(str);
gets(ptr);
int len1=strlen(str);
int len2=strlen(ptr);
printf("%d %d\n",kmp_Search(len1,len2),kmp_Count(len1,len2));
}
return 0;
}

1. 引言

    本KMP原文最初寫於2年多前的2011年12月，因當時初次接觸KMP，思路混亂導致寫也寫得混亂。所以一直想找機會重新寫下KMP，但苦於一直以來對KMP的理解始終不夠，故才遲遲沒有修改本文。

    然近期因開了個演算法班，班上專門講解資料結構、面試、演算法，才再次仔細回顧了這個KMP，在綜合了一些網友的理解、以及演算法班的兩位講師朋友曹博、鄒博的理解之後，寫了9張PPT，發在微博上。隨後，一不做二不休，索性將PPT上的內容整理到了本文之中（後來文章越寫越完整，所含內容早已不再是九張PPT 那樣簡單了）。

    KMP本身不復雜，但網上絕大部分的文章（包括本文的2011年版本）把它講混亂了。下面，咱們從暴力匹配演算法講起，隨後闡述KMP的流程 步驟、next 陣列的簡單求解 遞推原理 程式碼求解，接著基於next 陣列匹配，談到有限狀態自動機，next 陣列的優化，KMP的時間複雜度分析，最後簡要介紹兩個KMP的擴充套件演算法。

    全文力圖給你一個最為完整最為清晰的KMP，希望更多的人不再被KMP折磨或糾纏，不再被一些混亂的文章所混亂。有何疑問，歡迎隨時留言評論，thanks。

2. 暴力匹配演算法

    假設現在我們面臨這樣一個問題：有一個文字串S，和一個模式串P，現在要查詢P在S中的位置，怎麼查詢呢？

    如果用暴力匹配的思路，並假設現在文字串S匹配到 i 位置，模式串P匹配到 j 位置，則有：

  • 如果當前字元匹配成功（即S[i] == P[j]），則i++，j++，繼續匹配下一個字元；
  • 如果失配（即S[i]! = P[j]），令i = i - (j - 1)，j = 0。相當於每次匹配失敗時，i 回溯，j 被置為0。
    理清楚了暴力匹配演算法的流程及內在的邏輯，咱們可以寫出暴力匹配的程式碼，如下：[cpp] view plain copy print?
  1. int ViolentMatch(char* s, char* p)  
  2. {  
  3.     int sLen = strlen(s);  
  4.     int pLen = strlen(p);  
  5.     int i = 0;  
  6.     int j = 0;  
  7.     while (i < sLen && j < pLen)  
  8.     {  
  9.         if (s[i] == p[j])  
  10.         {  
  11.             //①如果當前字元匹配成功（即S[i] == P[j]），則i++，j++    
  12.             i++;  
  13.             j++;  
  14.         }  
  15.         else
  16.         {  
  17.             //②如果失配（即S[i]! = P[j]），令i = i - (j - 1)，j = 0    
  18.             i = i - j + 1;  
  19.             j = 0;  
  20.         }  
  21.     }  
  22.     //匹配成功，返回模式串p在文字串s中的位置，否則返回-1
  23.     if (j == pLen)  
  24.         return i - j;  
  25.     else
  26.         return -1;  
  27. }  
int ViolentMatch(char* s, char* p)
{
	int sLen = strlen(s);
	int pLen = strlen(p);

	int i = 0;
	int j = 0;
	while (i < sLen && j < pLen)
	{
		if (s[i] == p[j])
		{
			//①如果當前字元匹配成功（即S[i] == P[j]），則i++，j++    
			i++;
			j++;
		}
		else
		{
			//②如果失配（即S[i]! = P[j]），令i = i - (j - 1)，j = 0    
			i = i - j + 1;
			j = 0;
		}
	}
	//匹配成功，返回模式串p在文字串s中的位置，否則返回-1
	if (j == pLen)
		return i - j;
	else
		return -1;
}

    舉個例子，如果給定文字串S“BBC ABCDAB ABCDABCDABDE”，和模式串P“ABCDABD”，現在要拿模式串P去跟文字串S匹配，整個過程如下所示：

    1. S[0]為B，P[0]為A，不匹配，執行第②條指令：“如果失配（即S[i]! = P[j]），令i = i - (j - 1)，j = 0”，S[1]跟P[0]匹配，相當於模式串要往右移動一位（i=1，j=0）

    2. S[1]跟P[0]還是不匹配，繼續執行第②條指令：“如果失配（即S[i]! = P[j]），令i = i - (j - 1)，j = 0”，S[2]跟P[0]匹配（i=2，j=0），從而模式串不斷的向右移動一位（不斷的執行“令i = i - (j - 1)，j = 0”，i從2變到4，j一直為0）

    3. 直到S[4]跟P[0]匹配成功（i=4，j=0），此時按照上面的暴力匹配演算法的思路，轉而執行第①條指令：“如果當前字元匹配成功（即S[i] == P[j]），則i++，j++”，可得S[i]為S[5]，P[j]為P[1]，即接下來S[5]跟P[1]匹配（i=5，j=1）

     

    4. S[5]跟P[1]匹配成功，繼續執行第①條指令：“如果當前字元匹配成功（即S[i] == P[j]），則i++，j++”，得到S[6]跟P[2]匹配（i=6，j=2），如此進行下去

    

    5. 直到S[10]為空格字元，P[6]為字元D（i=10，j=6），因為不匹配，重新執行第②條指令：“如果失配（即S[i]! = P[j]），令i = i - (j - 1)，j = 0”，相當於S[5]跟P[0]匹配（i=5，j=0）

     

    6. 至此，我們可以看到，如果按照暴力匹配演算法的思路，儘管之前文字串和模式串已經分別匹配到了S[9]、P[5]，但因為S[10]跟P[6]不匹配，所以文字串回溯到S[5]，模式串回溯到P[0]，從而讓S[5]跟P[0]匹配。

    而S[5]肯定跟P[0]失配。為什麼呢？因為在之前第4步匹配中，我們已經得知S[5] = P[1] = B，而P[0] = A，即P[1] != P[0]，故S[5]必定不等於P[0]，所以回溯過去必然會導致失配。那有沒有一種演算法，讓i 不往回退，只需要移動j 即可呢？

    答案是肯定的。這種演算法就是本文的主旨KMP演算法，它利用之前已經部分匹配這個有效資訊，保持i 不回溯，通過修改j 的位置，讓模式串儘量地移動到有效的位置。

3. KMP演算法

3.1 定義

    Knuth-Morris-Pratt 字串查詢演算法，簡稱為 “KMP演算法”，常用於在一個文字串S內查詢一個模式串P 的出現位置，這個演算法由Donald Knuth、Vaughan Pratt、James H. Morris三人於1977年聯合發表，故取這3人的姓氏命名此演算法。    下面先直接給出KMP的演算法流程（如果感到一點點不適，沒關係，堅持下，稍後會有具體步驟及解釋，越往後看越會柳暗花明☺）：
  • 假設現在文字串S匹配到 i 位置，模式串P匹配到 j 位置
    • 如果j = -1，或者當前字元匹配成功（即S[i] == P[j]），都令i++，j++，繼續匹配下一個字元；
    • 如果j != -1，且當前字元匹配失敗（即S[i] != P[j]），則令 i 不變，j = next[j]。此舉意味著失配時，模式串P相對於文字串S向右移動了j - next [j] 位。
      • 換言之，當匹配失敗時，模式串向右移動的位數為：失配字元所在位置 - 失配字元對應的next 值（next 陣列的求解會在下文的3.3.3節中詳細闡述），即移動的實際位數為：j - next[j]，且此值大於等於1。
    很快，你也會意識到next 陣列各值的含義：代表當前字元之前的字串中，有多大長度的相同字首字尾。例如如果next [j] = k，代表j 之前的字串中有最大長度為k 的相同字首字尾。    此也意味著在某個字元失配時，該字元對應的next 值會告訴你下一步匹配中，模式串應該跳到哪個位置（跳到next [j] 的位置）。如果next [j] 等於0或-1，則跳到模式串的開頭字元，若next [j] = k 且 k > 0，代表下次匹配跳到j 之前的某個字元，而不是跳到開頭，且具體跳過了k 個字元。    轉換成程式碼表示，則是：[cpp] view plain copy print?
  1. int KmpSearch(char* s, char* p)  
  2. {  
  3.     int i = 0;  
  4.     int j = 0;  
  5.     int sLen = strlen(s);  
  6.     int pLen = strlen(p);  
  7.     while (i < sLen && j < pLen)  
  8.     {  
  9.         //①如果j = -1，或者當前字元匹配成功（即S[i] == P[j]），都令i++，j++    
  10.         if (j == -1 || s[i] == p[j])  
  11.         {  
  12.             i++;  
  13.             j++;  
  14.         }  
  15.         else
  16.         {  
  17.             //②如果j != -1，且當前字元匹配失敗（即S[i] != P[j]），則令 i 不變，j = next[j]    
  18.             //next[j]即為j所對應的next值      
  19.             j = next[j];  
  20.         }  
  21.     }  
  22.     if (j == pLen)  
  23.         return i - j;  
  24.     else
  25.         return -1;  
  26. }  
int KmpSearch(char* s, char* p)
{
	int i = 0;
	int j = 0;
	int sLen = strlen(s);
	int pLen = strlen(p);
	while (i < sLen && j < pLen)
	{
		//①如果j = -1，或者當前字元匹配成功（即S[i] == P[j]），都令i++，j++    
		if (j == -1 || s[i] == p[j])
		{
			i++;
			j++;
		}
		else
		{
			//②如果j != -1，且當前字元匹配失敗（即S[i] != P[j]），則令 i 不變，j = next[j]    
			//next[j]即為j所對應的next值      
			j = next[j];
		}
	}
	if (j == pLen)
		return i - j;
	else
		return -1;
}
    繼續拿之前的例子來說，當S[10]跟P[6]匹配失敗時，KMP不是跟暴力匹配那樣簡單的把模式串右移一位，而是執行第②條指令：“如果j != -1，且當前字元匹配失敗（即S[i] != P[j]），則令 i 不變，j = next[j]”，即j 從6變到2（後面我們將求得P[6]，即字元D對應的next 值為2），所以相當於模式串向右移動的位數為j - next[j]（j - next[j] = 6-2 = 4）。
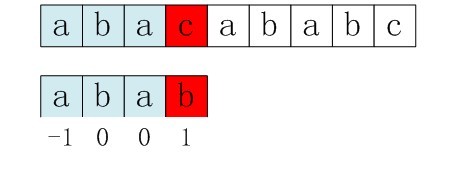
    向右移動4位後，S[10]跟P[2]繼續匹配。為什麼要向右移動4位呢，因為移動4位後，模式串中又有個“AB”可以繼續跟S[8]S[9]對應著，從而不用讓i 回溯。相當於在除去字元D的模式串子串中尋找相同的字首和字尾，然後根據字首字尾求出next 陣列，最後基於next 陣列進行匹配（不關心next 陣列是怎麼求來的，只想看匹配過程是咋樣的，可直接跳到下文3.3.4節）。

3.2 步驟

  • ①尋找字首字尾最長公共元素長度
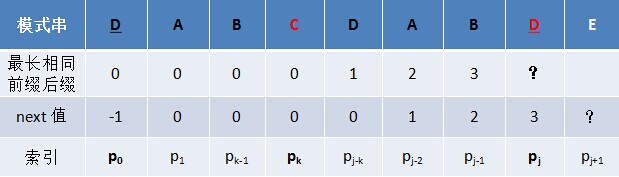
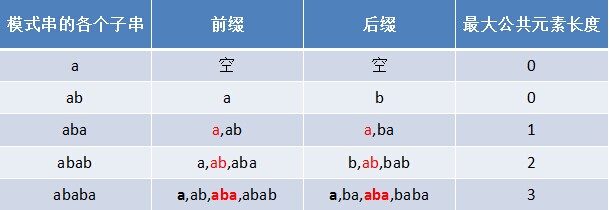
    • 對於P = p0 p1 ...pj-1 pj，尋找模式串P中長度最大且相等的字首和字尾。如果存在p0 p1 ...pk-1 pk = pj- k pj-k+1...pj-1 pj，那麼在包含pj的模式串中有最大長度為k+1的相同字首字尾。舉個例子，如果給定的模式串為“abab”，那麼它的各個子串的字首字尾的公共元素的最大長度如下表格所示：

比如對於字串aba來說，它有長度為1的相同字首字尾a；而對於字串abab來說，它有長度為2的相同字首字尾ab（相同字首字尾的長度為k + 1，k + 1 = 2）。

  • ②求next陣列
    • next 陣列考慮的是除當前字元外的最長相同字首字尾，所以通過第①步驟求得各個字首字尾的公共元素的最大長度後，只要稍作變形即可：將第①步驟中求得的值整體右移一位，然後初值賦為-1，如下表格所示：

比如對於aba來說，第3個字元a之前的字串ab中有長度為0的相同字首字尾，所以第3個字元a對應的next值為0；而對於abab來說，第4個字元b之前的字串aba中有長度為1的相同字首字尾a，所以第4個字元b對應的next值為1（相同字首字尾的長度為k，k = 1）。

  • ③根據next陣列進行匹配
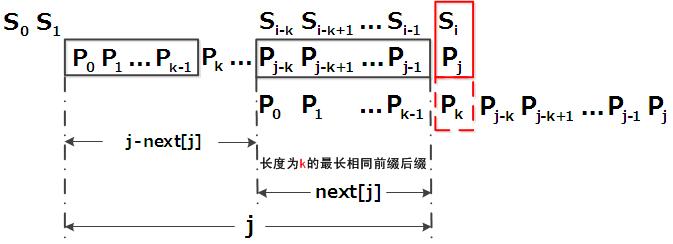
    • 匹配失配，j = next [j]，模式串向右移動的位數為：j - next[j]。換言之，當模式串的字尾pj-k pj-k+1, ..., pj-1 跟文字串si-k si-k+1, ..., si-1匹配成功，但pj 跟si匹配失敗時，因為next[j] = k，相當於在不包含pj的模式串中有最大長度為k 的相同字首字尾，即p0 p1 ...pk-1 = pj-k pj-k+1...pj-1，故令j = next[j]，從而讓模式串右移j - next[j] 位，使得模式串的字首p0 p1, ..., pk-1對應著文字串 si-k si-k+1, ..., si-1，而後讓pk 跟si 繼續匹配。如下圖所示：
    綜上，KMP的next 陣列相當於告訴我們：當模式串中的某個字元跟文字串中的某個字元匹配失配時，模式串下一步應該跳到哪個位置。如模式串中在j 處的字元跟文字串在i 處的字元匹配失配時，下一步用next [j] 處的字元繼續跟文字串i 處的字元匹配，相當於模式串向右移動 j - next[j] 位。    接下來，分別具體解釋上述3個步驟。

3.3 解釋

3.3.1 尋找最長字首字尾

    如果給定的模式串是：“ABCDABD”，從左至右遍歷整個模式串，其各個子串的字首字尾分別如下表格所示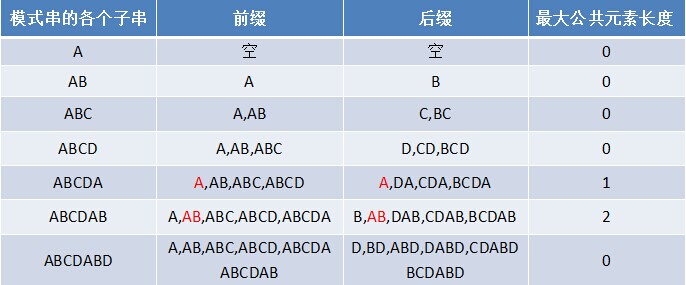：    也就是說，原模式串子串對應的各個字首字尾的公共元素的最大長度表為（下簡稱《最大長度表》）：

3.3.2 基於《最大長度表》匹配

因為模式串中首尾可能會有重複的字元，故可得出下述結論：
失配時，模式串向右移動的位數為：已匹配字元數 - 失配字元的上一位字元所對應的最大長度值

    下面，咱們就結合之前的《最大長度表》和上述結論，進行字串的匹配。如果給定文字串“BBC ABCDAB ABCDABCDABDE”，和模式串“ABCDABD”，現在要拿模式串去跟文字串匹配，如下圖所示：

        

  • 1. 因為模式串中的字元A跟文字串中的字元B、B、C、空格一開始就不匹配，所以不必考慮結論，直接將模式串不斷的右移一位即可，直到模式串中的字元A跟文字串的第5個字元A匹配成功：

  • 2. 繼續往後匹配，當模式串最後一個字元D跟文字串匹配時失配，顯而易見，模式串需要向右移動。但向右移動多少位呢？因為此時已經匹配的字元數為6個（ABCDAB），然後根據《最大長度表》可得失配字元D的上一位字元B對應的長度值為2，所以根據之前的結論，可知需要向右移動6 - 2 = 4 位。
  • 3. 模式串向右移動4位後，發現C處再度失配，因為此時已經匹配了2個字元（AB），且上一位字元B對應的最大長度值為0，所以向右移動：2 - 0 =2 位。
           
  • 4. A與空格失配，向右移動1 位。
  • 5. 繼續比較，發現D與C 失配，故向右移動的位數為：已匹配的字元數6減去上一位字元B對應的最大長度2，即向右移動6 - 2 = 4 位。
           
  • 6. 經歷第5步後，發現匹配成功，過程結束。

         

    通過上述匹配過程可以看出，問題的關鍵就是尋找模式串中最大長度的相同字首和字尾，找到了模式串中每個字元之前的字首和字尾公共部分的最大長度後，便可基於此匹配。而這個最大長度便正是next 陣列要表達的含義。

3.3.3 根據《最大長度表》求next 陣列

    由上文，我們已經知道，字串“ABCDABD”各個字首字尾的最大公共元素長度分別為：

    而且，根據這個表可以得出下述結論

  • 失配時，模式串向右移動的位數為：已匹配字元數 - 失配字元的上一位字元所對應的最大長度值
    上文利用這個表和結論進行匹配時，我們發現，當匹配到一個字元失配時，其實沒必要考慮當前失配的字元，更何況我們每次失配時，都是看的失配字元的上一位字元對應的最大長度值。如此，便引出了next 陣列。    給定字串“ABCDABD”，可求得它的next 陣列如下：

    把next 陣列跟之前求得的最大長度表對比後，不難發現，next 陣列相當於“最大長度值” 整體向右移動一位，然後初始值賦為-1。意識到了這一點，你會驚呼原來next 陣列的求解竟然如此簡單：就是找最大對稱長度的字首字尾，然後整體右移一位，初值賦為-1（當然，你也可以直接計算某個字元對應的next值，就是看這個字元之前的字串中有多大長度的相同字首字尾）。

    換言之，對於給定的模式串：ABCDABD，它的最大長度表及next 陣列分別如下：


    根據最大長度表求出了next 陣列後，從而有

失配時，模式串向右移動的位數為：失配字元所在位置 - 失配字元對應的next 值

    而後，你會發現，無論是基於《最大長度表》的匹配，還是基於next 陣列的匹配，兩者得出來的向右移動的位數是一樣的。為什麼呢？因為：

  • 根據《最大長度表》，失配時，模式串向右移動的位數 = 已經匹配的字元數 - 失配字元的上一位字元的最大長度值
  • 而根據《next 陣列》，失配時，模式串向右移動的位數 = 失配字元的位置 - 失配字元對應的next 值
    • 其中，從0開始計數時，失配字元的位置 = 已經匹配的字元數（失配字元不計數），而失配字元對應的next 值 = 失配字元的上一位字元的最大長度值，兩相比較，結果必然完全一致。

    所以，你可以把《最大長度表》看做是next 陣列的雛形，甚至就把它當做next 陣列也是可以的，區別不過是怎麼用的問題。

3.3.4 通過程式碼遞推計算next 陣列

    接下來，咱們來寫程式碼求下next 陣列。

    基於之前的理解，可知計算next 陣列的方法可以採用遞推：

  • 1. 如果對於值k，已有p0 p1, ..., pk-1 = pj-k pj-k+1, ..., pj-1，相當於next[j] = k。
    • 此意味著什麼呢？究其本質，next[j] = k 代表p[j] 之前的模式串子串中，有長度為k 的相同字首和字尾。有了這個next 陣列，在KMP匹配中，當模式串中j 處的字元失配時，下一步用next[j]處的字元繼續跟文字串匹配，相當於模式串向右移動j - next[j] 位。

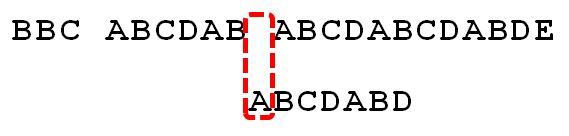
舉個例子，如下圖，根據模式串“ABCDABD”的next 陣列可知失配位置的字元D對應的next 值為2，代表字元D前有長度為2的相同字首和字尾（這個相同的字首字尾即為“AB”），失配後，模式串需要向右移動j - next [j] = 6 - 2 =4位。

向右移動4位後，模式串中的字元C繼續跟文字串匹配。

  • 2. 下面的問題是：已知next [0, ..., j]，如何求出next [j + 1]呢？

    對於P的前j+1個序列字元：

  • 若p[k] == p[j]，則next[j + 1 ] = next [j] + 1 = k + 1；
  • 若p[k ] ≠ p[j]，如果此時p[ next[k] ] == p[j ]，則next[ j + 1 ] =  next[k] + 1，否則繼續遞迴字首索引k = next[k]，而後重複此過程。 相當於在字元p[j+1]之前不存在長度為k+1的字首"p0 p1, …, pk-1 pk"跟字尾“pj-k pj-k+1, …, pj-1 pj"相等，那麼是否可能存在另一個值t+1 < k+1，使得長度更小的字首 “p0 p1, …, pt-1 pt” 等於長度更小的字尾 “pj-t pj-t+1, …, pj-1 pj” 呢？如果存在，那麼這個t+1 便是next[ j+1]的值，此相當於利用已經求得的next 陣列（next [0, ..., k, ..., j]）進行P串字首跟P串字尾的匹配。
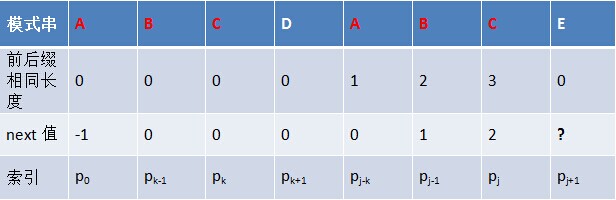
   一般的文章或教材可能就此一筆帶過，但大部分的初學者可能還是不能很好的理解上述求解next 陣列的原理，故接下來，我再來著重說明下。    如下圖所示，假定給定模式串ABCDABCE，且已知next [j] = k（相當於“p0 pk-1” = “pj-k pj-1” = AB，可以看出k為2），現要求next [j + 1]等於多少？因為pk = pj = C，所以next[j + 1] = next[j] + 1 = k + 1（可以看出next[j + 1] = 3）。代表字元E前的模式串中，有長度k+1 的相同字首字尾。

    但如果pk != pj 呢？說明“p0 pk-1 pk”  ≠ “pj-k pj-1 pj”。換言之，當pk != pj後，字元E前有多大長度的相同字首字尾呢？很明顯，因為C不同於D，所以ABC 跟 ABD不相同，即字元E前的模式串沒有長度為k+1的相同字首字尾，也就不能再簡單的令：next[j + 1] = next[j] + 1 。所以，咱們只能去尋找長度更短一點的相同字首字尾。

    結合上圖來講，若能在字首“ p0 pk-1 pk ” 中不斷的遞迴字首索引k = next [k]，找到一個字元pk’ 也為D，代表pk’ = pj，且滿足p0 pk'-1 pk' = pj-k' pj-1 pj，則最大相同的字首字尾長度為k' + 1，從而next [j + 1] = k’ + 1 = next [k' ] + 1。否則字首中沒有D，則代表沒有相同的字首字尾，next [j + 1] = 0。    那為何遞迴字首索引k = next[k]，就能找到長度更短的相同字首字尾呢？這又歸根到next陣列的含義。我們拿字首 p0 pk-1 pk 去跟字尾pj-k pj-1 pj匹配，如果pk 跟pj 失配，下一步就是用p[next[k]] 去跟pj 繼續匹配，如果p[ next[k] ]跟pj還是不匹配，則需要尋找長度更短的相同字首字尾，即下一步用p[ next[ next[k] ] ]去跟pj匹配。此過程相當於模式串的自我匹配，所以不斷的遞迴k = next[k]，直到要麼找到長度更短的相同字首字尾，要麼沒有長度更短的相同字首字尾。如下圖所示：   
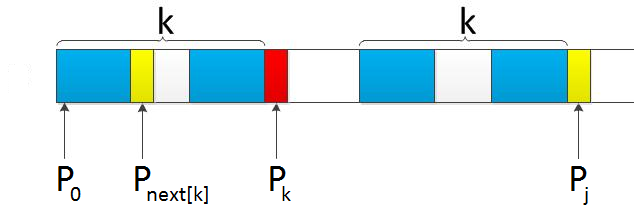
    所以，因最終在字首ABC中沒有找到D，故E的next 值為0：
模式串的字尾：ABDE
模式串的字首：ABC
字首右移兩位：     ABC
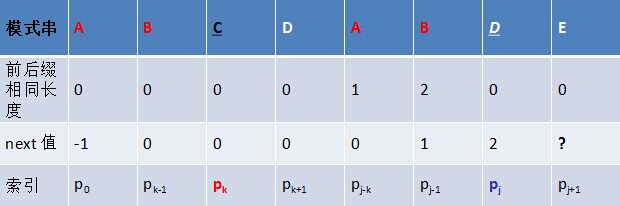
    讀到此，有的讀者可能又有疑問了，那能否舉一個能在字首中找到字元D的例子呢？OK，咱們便來看一個能在字首中找到字元D的例子，如下圖所示：
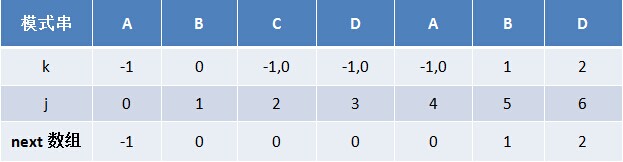
    給定模式串DABCDABDE，我們很順利的求得字元D之前的“DABCDAB”的各個子串的最長相同字首字尾的長度分別為0 0 0 0 1 2 3，但當遍歷到字元D，要求包括D在內的“DABCDABD”最長相同字首字尾時，我們發現pj處的字元D跟pk處的字元C不一樣，換言之，字首DABC的最後一個字元C 跟字尾DABD的最後一個字元D不相同，所以不存在長度為4的相同字首字尾。    怎麼辦呢？既然沒有長度為4的相同字首字尾，咱們可以尋找長度短點的相同字首字尾，最終，因在p0處發現也有個字元D，p0 = pj，所以p[j]對應的長度值為1，相當於E對應的next 值為1（即字元E之前的字串“DABCDABD”中有長度為1的相同字首和字尾）。    綜上，可以通過遞推求得next 陣列，程式碼如下所示：[cpp] view plain copy print?
  1. void GetNext(char* p,int next[])  
  2. {  
  3.     int pLen = strlen(p);  
  4.     next[0] = -1;  
  5.     int k = -1;  
  6.     int j = 0;  
  7.     while (j < pLen - 1)  
  8.     {  
  9.         //p[k]表示字首，p[j]表示字尾
  10.         if (k == -1 || p[j] == p[k])   
  11.         {  
  12.             ++k;  
  13.             ++j;  
  14.             next[j] = k;  
  15.         }  
  16.         else
  17.         {  
  18.             k = next[k];  
  19.         }  
  20.     }  
  21. }  
void GetNext(char* p,int next[])
{
	int pLen = strlen(p);
	next[0] = -1;
	int k = -1;
	int j = 0;
	while (j < pLen - 1)
	{
		//p[k]表示字首，p[j]表示字尾
		if (k == -1 || p[j] == p[k]) 
		{
			++k;
			++j;
			next[j] = k;
		}
		else 
		{
			k = next[k];
		}
	}
}

    用程式碼重新計算下“ABCDABD”的next 陣列，以驗證之前通過“最長相同字首字尾長度值右移一位，然後初值賦為-1”得到的next 陣列是否正確，計算結果如下表格所示：


    從上述表格可以看出，無論是之前通過“最長相同字首字尾長度值右移一位，然後初值賦為-1”得到的next 陣列，還是之後通過程式碼遞推計算求得的next 陣列，結果是完全一致的。

3.3.5 基於《next 陣列》匹配

    下面，我們來基於next 陣列進行匹配。

    還是給定文字串“BBC ABCDAB ABCDABCDABDE”，和模式串“ABCDABD”，現在要拿模式串去跟文字串匹配，如下圖所示：

    在正式匹配之前，讓我們來再次回顧下上文2.1節所述的KMP演算法的匹配流程：

  • “假設現在文字串S匹配到 i 位置，模式串P匹配到 j 位置
    • 如果j = -1，或者當前字元匹配成功（即S[i] == P[j]），都令i++，j++，繼續匹配下一個字元；
    • 如果j != -1，且當前字元匹配失敗（即S[i] != P[j]），則令 i 不變，j = next[j]。此舉意味著失配時，模式串P相對於文字串S向右移動了j - next [j] 位。
      • 換言之，當匹配失敗時，模式串向右移動的位數為：失配字元所在位置 - 失配字元對應的next 值，即移動的實際位數為：j - next[j]，且此值大於等於1。”
  • 1. 最開始匹配時
    • P[0]跟S[0]匹配失敗
      • 所以執行“如果j != -1，且當前字元匹配失敗（即S[i] != P[j]），則令 i 不變，j = next[j]”，所以j = -1，故轉而執行“如果j = -1，或者當前字元匹配成功（即S[i] == P[j]），都令i++，j++”，得到i = 1，j = 0，即P[0]繼續跟S[1]匹配。
    • P[0]跟S[1]又失配，j再次等於-1，i、j繼續自增，從而P[0]跟S[2]匹配。
    • P[0]跟S[2]失配後，P[0]又跟S[3]匹配。
    • P[0]跟S[3]再失配，直到P[0]跟S[4]匹配成功，開始執行此條指令的後半段：“如果j = -1，或者當前字元匹配成功（即S[i] == P[j]），都令i++，j++”。
  • 2. P[1]跟S[5]匹配成功，P[2]跟S[6]也匹配成功, ...，直到當匹配到P[6]處的字元D時失配（即S[10] != P[6]），由於P[6]處的D對應的next 值為2，所以下一步用P[2]處的字元C繼續跟S[10]匹配，相當於向右移動：j - next[j] = 6 - 2 =4 位。

  • 3. 向右移動4位後，P[2]處的C再次失配，由於C對應的next值為0，所以下一步用P[0]處的字元繼續跟S[10]匹配，相當於向右移動：j - next[j] = 2 - 0 = 2 位。

  • 4. 移動兩位之後，A 跟空格不匹配，模式串後移1 位。

  • 5. P[6]處的D再次失配，因為P[6]對應的next值為2，故下一步用P[2]繼續跟文字串匹配，相當於模式串向右移動 j - next[j] = 6 - 2 = 4 位。
  • 6. 匹配成功，過程結束。

    匹配過程一模一樣。也從側面佐證了，next 陣列確實是只要將各個最大字首字尾的公共元素的長度值右移一位，且把初值賦為-1 即可。

3.3.6 基於《最大長度表》與基於《next 陣列》等價

    我們已經知道，利用next 陣列進行匹配失配時，模式串向右移動 j - next [ j ] 位，等價於已匹配字元數 - 失配字元的上一位字元所對應的最大長度值。原因是：

  1. j 從0開始計數，那麼當數到失配字元時，j 的數值就是已匹配的字元數；
  2. 由於next 陣列是由最大長度值表整體向右移動一位（且初值賦為-1）得到的，那麼失配字元的上一位字元所對應的最大長度值，即為當前失配字元的next 值。

    但為何本文不直接利用next 陣列進行匹配呢？因為next 陣列不好求，而一個字串的字首字尾的公共元素的最大長度值很容易求。例如若給定模式串“ababa”，要你快速口算出其next 陣列，乍一看，每次求對應字元的next值時，還得把該字元排除之外，然後看該字元之前的字串中有最大長度為多大的相同字首字尾，此過程不夠直接。而如果讓你求其字首字尾公共元素的最大長度，則很容易直接得出結果：0 0 1 2 3，如下表格所示：

    然後這5個數字 全部整體右移一位，且初值賦為-1，即得到其next 陣列：-1 0 0 1 2。

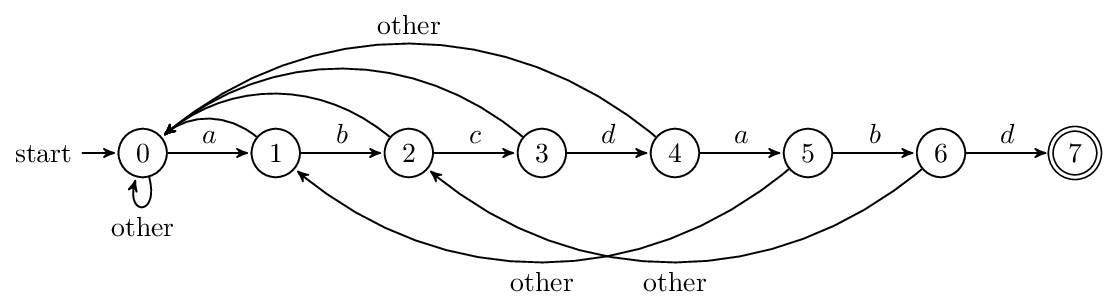
3.3.7 Next 陣列與有限狀態自動機

    next 負責把模式串向前移動，且當第j位不匹配的時候，用第next[j]位和主串匹配，就像打了張“表”。此外，next 也可以看作有限狀態自動機的狀態，在已經讀了多少字元的情況下，失配後，前面讀的若干個字元是有用的。


3.3.8 Next 陣列的優化

   行文至此，咱們全面瞭解了暴力匹配的思路、KMP演算法的原理、流程、流程之間的內在邏輯聯絡，以及next 陣列的簡單求解（《最大長度表》整體右移一位，然後初值賦為-1）和程式碼求解，最後基於《next 陣列》的匹配，看似洋洋灑灑，清晰透徹，但以上忽略了一個小問題。

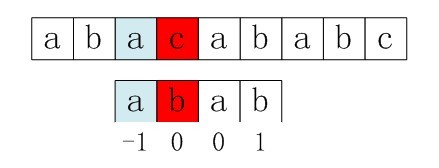
    比如，如果用之前的next 陣列方法求模式串“abab”的next 陣列，可得其next 陣列為-1 0 0 1（0 0 1 2整體右移一位，初值賦為-1），當它跟下圖中的文字串去匹配的時候，發現b跟c失配，於是模式串右移j - next[j] = 3 - 1 =2位。

    右移2位後，b又跟c失配。事實上，因為在上一步的匹配中，已經得知p[3] = b，與s[3] = c失配，而右移兩位之後，讓p[ next[3] ] = p[1] = b 再跟s[3]匹配時，必然失配。問題出在哪呢？

   

    問題出在不該出現p[j] = p[ next[j] ]。為什麼呢？理由是：當p[j] != s[i] 時，下次匹配必然是p[ next [j]] 跟s[i]匹配，如果p[j] = p[ next[j] ]，必然導致後一步匹配失敗（因為p[j]已經跟s[i]失配，然後你還用跟p[j]等同的值p[next[j]]去跟s[i]匹配，很顯然，必然失配），所以不能允許p[j] = p[ next[j ]]。如果出現了p[j] = p[ next[j] ]咋辦呢？如果出現了，則需要再次遞迴，即令next[j] = next[ next[j] ]。

    所以，咱們得修改下求next 陣列的程式碼。[cpp] view plain copy print?
  1. //優化過後的next 陣列求法
  2. void GetNextval(char* p, int next[])  
  3. {  
  4.     int pLen = strlen(p);  
  5.     next[0] = -1;  
  6.     int k = -1;  
  7.     int j = 0;  
  8.     while (j < pLen - 1)  
  9.     {  
  10.         //p[k]表示字首，p[j]表示字尾  
  11.         if (k == -1 || p[j] == p[k])  
  12.         {  
  13.             ++j;  
  14.             ++k;  
  15.             //較之前next陣列求法，改動在下面4行
  16.             if (p[j] != p[k])  
  17.                 next[j] = k;   //之前只有這一行
  18.             else
  19.                 //因為不能出現p[j] = p[ next[j ]]，所以當出現時需要繼續遞迴，k = next[k] = next[next[k]]
  20.                 next[j] = next[k];  
  21.         }  
  22.         else
  23.         {  
  24.             k = next[k];  
  25.         }  
  26.     }  
  27. }  
//優化過後的next 陣列求法
void GetNextval(char* p, int next[])
{
	int pLen = strlen(p);
	next[0] = -1;
	int k = -1;
	int j = 0;
	while (j < pLen - 1)
	{
		//p[k]表示字首，p[j]表示字尾  
		if (k == -1 || p[j] == p[k])
		{
			++j;
			++k;
			//較之前next陣列求法，改動在下面4行
			if (p[j] != p[k])
				next[j] = k;   //之前只有這一行
			else
				//因為不能出現p[j] = p[ next[j ]]，所以當出現時需要繼續遞迴，k = next[k] = next[next[k]]
				next[j] = next[k];
		}
		else
		{
			k = next[k];
		}
	}
}

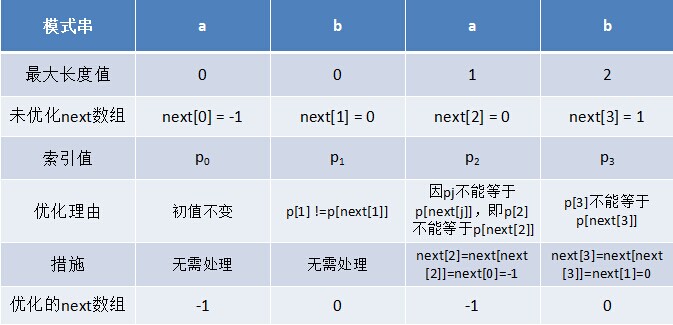
    利用優化過後的next 陣列求法，可知模式串“abab”的新next陣列為：-1 0 -1 0。可能有些讀者會問：原始next 陣列是字首字尾最長公共元素長度值右移一位， 然後初值賦為-1而得，那麼優化後的next 陣列如何快速心算出呢？實際上，只要求出了原始next 陣列，便可以根據原始next 陣列快速求出優化後的next 陣列。還是以abab為例，如下表格所示：

    

只要出現了p[next[j]] = p[j]的情況，則把next[j]的值再次遞迴。例如在求模式串“abab”的第2個a的next值時，如果是未優化的next值的話，第2個a對應的next值為0，相當於第2個a失配時，下一步匹配模式串會用p[0]處的a再次跟文字串匹配，必然失配。所以求第2個a的next值時，需要再次遞迴：next[2] = next[ next[2] ] = next[0] = -1（此後，根據優化後的新next值可知，第

相關推薦

KMP匹配詳細講解+next陣列真正理解

之前轉載過一篇kuangbin大佬的kmp模板，只會用，但是不清楚原理現在看了某大佬的文章，發現講解的非常精彩，但是有一點不足就是沒講清楚KMP時間複雜度問題，但是自己的語言組織能力以及理解能力也不是很好，所以就直接copyt過來了。希望_july_v博主不介意。http:/

【經典演算法】——KMP，深入講解next陣列的求解

前言　　 　　之前對kmp演算法雖然瞭解它的原理，即求出P0···Pi的最大相同前後綴長度k；但是問題在於如何求出這個最大前後綴長度呢？我覺得網上很多帖子都說的不是很清楚，總感覺沒有把那層紙戳破，後來翻看演算法導論，32章 字串匹配雖然講到了對前字尾計算的正確性，但是大量的推理證明不大好理解，沒有與程式結合

字串匹配——KMP演算法中的next陣列理解

關於原理就不講了，只說下我對Next陣列的理解，希望可以讓你獲得靈光一閃。 其實最難的就是是j=Next[j];這麼一句話，當時思考了很長時間，終於明白的時候確實很興奮加得意。 #include<cstdio> #include<cstring> v

KMP演算法中關於next陣列的j=next[j]理解

這篇文章是在oneNote上寫的，小弟不懂oneNote怎麼轉成md，所以只能笨辦法截圖上來了。。。覺得看的費勁的可以找我要原本 聯絡方式郵箱： [email protected]

面向考研——計算KMP演算法中的next陣列和nextval陣列

KMP演算法中，如何手動求next陣列和nextval陣列？ 首先我們要理解next陣列的意義，為了實現更加高效的字元匹配，next陣列是用來尋找字串陣列內部的自身的一種規律，利用字串內部的一種相似性，來優化字串陣列匹配演算法。所以才需要計算這麼一個next陣列來幫助演算法

KMP演算法詳細講解

文章篇幅有點長，但是最後一張圖真的很棒，希望讀者堅持慢慢看到最後，必有收穫。 字串單模式問題描述： 給定文字串text,和模式串pattern,在文字串text中找到模式串pattern第一次出現的位置。 一、最基本的字串單模式匹配演算法：暴力求解（Brute

比較好懂的KMP演算法解釋(附next陣列求解方法）

字串匹配是計算機的基本任務之一。 　　舉例來說，有一個字串"BBC ABCDAB ABCDABCDABDE"，我想知道，裡面是否包含另一個字串"ABCDABD"？ 　　許多演算法可以完成這個任務，Knuth-Morris-Pratt演算法（簡稱KMP）是最常用的之一。它以

C++ 物件模型詳細講解（特別容易理解）

感謝，Thanks！                                          四 堆疊與函式呼叫 一 C++程式記憶體分配 1) 在棧上建立。在執行函式時，函式內區域性變數的儲存單元都在棧上建立，函式執行結束時這些儲存單元自動被釋放。棧記憶體分配運算內置於處理器的指令集中，

超詳細理解：kmp演算法next陣列求解過程和回溯的含義

前言 KMP演算法是用來求一個較長字串是否包含另一個較短字串的演算法。具體演算法下一篇寫吧，這篇主要解釋next陣列的求解。 程式碼 程式碼應該都看過了，先貼在這裡，其中最難理解的地方就是求next陣列，以及k往前回溯，這也是寫本文的目的。 in

kmp演算法 關於next陣列的詳細解釋

前言　　 　　之前對kmp演算法雖然瞭解它的原理，即求出P0···Pi的最大相同前後綴長度k；但是問題在於如何求出這個最大前後綴長度呢？我覺得網上很多帖子都說的不是很清楚，總感覺沒有把那層紙戳破，後來翻看演算法導論，32章 字串匹配雖然講到了對前後綴計算的正確性，但

簡單易懂的KMP，NEXT陣列，BF演算法（例項講解）！！！

去了360面試，問了一個關於KMP的知識點，呀，完全忘了啊，太不應該了，然後就打算看看這個KMP，，， 看了好多關於KMP演算法的書籍和資料，總感覺沒有說的很清楚，為什麼會產生next陣列，為什麼給出了那麼簡短的程式，沒有一個過程，而有的帖子雖然next及其字串匹配說的很清

字串匹配KMP演算法中Next[]陣列求法

int get_nextval(SString T,int &nextval[ ]){            //求模式串T的next函式修正值並存入陣列nextval。            i=1; nextval[1]=0; j=0;            while(i<T[0]){

字串匹配：求給定字串的next陣列以及KMP演算法

一、理解字串的next陣列值 next陣列值的概念涉及到字串匹配的問題，比較抽象，先介紹一些預備知識： （1）主串和模式串        例如我們想知道一個字串是否包含另一個字串時，如串S="bbc abcdab abcdabcdabde"中是否包含串s="abcdab

KMP演算法next陣列計算的理解——菜鳥福音

我的文章莫名找不到了。。。還是再寫一遍吧，希望對了解KMP的演算法有點幫助…… 首先寫幾點 1）本文討論的KMP主要是嚴蔚敏的《資料結構》中第四章提到的KMP，即帶NEXT[]輔助陣列的KMP演算法 2）本文主要是討論KMP演算法NEXT[]陣列的計算的理

對KMP算法通過代碼生成next數組理解

通過 [] get 下標 n-1 while 導致 代碼 如果 本文是根據考研數據結構2019版天勤高分筆記理解編寫的： 首先給出代碼： 1 void getnext(Str substr,int next[]){ 2 int i=0,j=0;

POJ 2752 Seek the Name, Seek the Fame(KMP的next陣列)

【連結】http://poj.org/problem?id=2752 【題意】給個字串，求這個串所有字首與字尾相同的所有綴長度 【思路】 其實kmp裡的next這個微妙的陣列本身就是答案了，至於為什麼，我是用以前不知道哪裡弄來的的kmp模板試了一下看出來的【喂

【HDU - 1867 】A + B for you again（KMP，next陣列應用）

題幹： Generally speaking, there are a lot of problems about strings processing. Now you encounter another such problem. If you get two strings, such

深入理解計算機系統 2.4.2 IEEE浮點表示詳細講解

定義 IEEE浮點標準用以下公式表示\(V = (-1)^s * M * 2^E\) 符號(sign)：s決定這書是負數(s = 1)還是正數(s = 0),而對於數值0的符號位解釋作為特殊情況處理 。 尾數(significand)：M是一個二進位制小數，它的範圍是\

KMP演算法模板 - 構建next最長字首陣列 與 kmp核心演算法

#include <iostream> #include <string> using namespace std; //構建next最長字首陣列 int* getNextArray(const string &sub) { if(sub.length() ==

搜尋匹配顯示例項—主要keyup事件和陣列的理解

要點： 1.相容程式碼的使用，這裡獨立遇到的第一個相容問題，並解決，有點開心。以前，自己寫相容程式碼，都是根據返回值跟 "undefined"比較，這裡直接跟 "string"比較型別，速度更快，用這個方法。 2.空陣列的建立，可以作為容器，也就就是接下來放入div中的資料。最後調試出現的問題是