【經典演算法】——KMP,深入講解next陣列的求解
前言
之前對kmp演算法雖然瞭解它的原理,即求出P0···Pi的最大相同前後綴長度k;但是問題在於如何求出這個最大前後綴長度呢?我覺得網上很多帖子都說的不是很清楚,總感覺沒有把那層紙戳破,後來翻看演算法導論,32章 字串匹配雖然講到了對前字尾計算的正確性,但是大量的推理證明不大好理解,沒有與程式結合起來講。今天我在這裡講一講我的一些理解,希望大家多多指教,如果有不清楚的或錯誤的請給我留言。
1.kmp演算法的原理:
字串匹配是計算機的基本任務之一。
舉例來說,有一個字串"BBC ABCDAB ABCDABCDABDE",我想知道,裡面是否包含另一個字串"ABCDABD"?

許多演算法可以完成這個任務,Knuth-Morris-Pratt演算法(簡稱KMP)是最常用的之一。它以三個發明者命名,起頭的那個K就是著名科學家Donald Knuth。

這種演算法不太容易理解,網上有很多解釋,但讀起來都很費勁。直到讀到Jake Boxer的文章,我才真正理解這種演算法。下面,我用自己的語言,試圖寫一篇比較好懂的KMP演算法解釋。
1.

首先,字串"BBC ABCDAB ABCDABCDABDE"的第一個字元與搜尋詞"ABCDABD"的第一個字元,進行比較。因為B與A不匹配,所以搜尋詞後移一位。
2.

因為B與A不匹配,搜尋詞再往後移。
3.

就這樣,直到字串有一個字元,與搜尋詞的第一個字元相同為止。
4.

接著比較字串和搜尋詞的下一個字元,還是相同。
5.

直到字串有一個字元,與搜尋詞對應的字元不相同為止。
6.

這時,最自然的反應是,將搜尋詞整個後移一位,再從頭逐個比較。這樣做雖然可行,但是效率很差,因為你要把"搜尋位置"移到已經比較過的位置,重比一遍。
7.

一個基本事實是,當空格與D不匹配時,你其實知道前面六個字元是"ABCDAB"。KMP演算法的想法是,設法利用這個已知資訊,不要把"搜尋位置"移回已經比較過的位置,繼續把它向後移,這樣就提高了效率。
8.

怎麼做到這一點呢?可以針對搜尋詞,算出一張《部分匹配表》(Partial Match Table)。這張表是如何產生的,後面再介紹,這裡只要會用就可以了。
9.

已知空格與D不匹配時,前面六個字元"ABCDAB"是匹配的。查表可知,最後一個匹配字元B對應的"部分匹配值"為2,因此按照下面的公式算出向後移動的位數:
移動位數 = 已匹配的字元數 - 對應的部分匹配值
因為 6 - 2 等於4,所以將搜尋詞向後移動4位。
10.

因為空格與C不匹配,搜尋詞還要繼續往後移。這時,已匹配的字元數為2("AB"),對應的"部分匹配值"為0。所以,移動位數 = 2 - 0,結果為 2,於是將搜尋詞向後移2位。
11.

因為空格與A不匹配,繼續後移一位。
12.

逐位比較,直到發現C與D不匹配。於是,移動位數 = 6 - 2,繼續將搜尋詞向後移動4位。
13.

逐位比較,直到搜尋詞的最後一位,發現完全匹配,於是搜尋完成。如果還要繼續搜尋(即找出全部匹配),移動位數 = 7 - 0,再將搜尋詞向後移動7位,這裡就不再重複了。
14.

下面介紹《部分匹配表》是如何產生的。
首先,要了解兩個概念:"字首"和"字尾"。 "字首"指除了最後一個字元以外,一個字串的全部頭部組合;"字尾"指除了第一個字元以外,一個字串的全部尾部組合。
15.

"部分匹配值"就是"字首"和"字尾"的最長的共有元素的長度。以"ABCDABD"為例,
- "A"的字首和字尾都為空集,共有元素的長度為0;
- "AB"的字首為[A],字尾為[B],共有元素的長度為0;
- "ABC"的字首為[A, AB],字尾為[BC, C],共有元素的長度0;
- "ABCD"的字首為[A, AB, ABC],字尾為[BCD, CD, D],共有元素的長度為0;
- "ABCDA"的字首為[A, AB, ABC, ABCD],字尾為[BCDA, CDA, DA, A],共有元素為"A",長度為1;
- "ABCDAB"的字首為[A, AB, ABC, ABCD, ABCDA],字尾為[BCDAB, CDAB, DAB, AB, B],共有元素為"AB",長度為2;
- "ABCDABD"的字首為[A, AB, ABC, ABCD, ABCDA, ABCDAB],字尾為[BCDABD, CDABD, DABD, ABD, BD, D],共有元素的長度為0。
16.

"部分匹配"的實質是,有時候,字串頭部和尾部會有重複。比如,"ABCDAB"之中有兩個"AB",那麼它的"部分匹配值"就是2("AB"的長度)。搜尋詞移動的時候,第一個"AB"向後移動4位(字串長度-部分匹配值),就可以來到第二個"AB"的位置。
2.next陣列的求解思路
通過上文完全可以對kmp演算法的原理有個清晰的瞭解,那麼下一步就是程式設計實現了,其中最重要的就是如何根據待匹配的模版字串求出對應每一位的最大相同前後綴的長度。我先給出我的程式碼:
1 void makeNext(const char P[],int next[]) 2 { 3 int q,k;//q:模版字串下標;k:最大前後綴長度 4 int m = strlen(P);//模版字串長度 5 next[0] = 0;//模版字串的第一個字元的最大前後綴長度為0 6 for (q = 1,k = 0; q < m; ++q)//for迴圈,從第二個字元開始,依次計算每一個字元對應的next值 7 { 8 while(k > 0 && P[q] != P[k])//遞迴的求出P[0]···P[q]的最大的相同的前後綴長度k 9 k = next[k-1]; //不理解沒關係看下面的分析,這個while迴圈是整段程式碼的精髓所在,確實不好理解 10 if (P[q] == P[k])//如果相等,那麼最大相同前後綴長度加1 11 { 12 k++; 13 } 14 next[q] = k; 15 } 16 }
現在我著重講解一下while迴圈所做的工作:
- 已知前一步計算時最大相同的前後綴長度為k(k>0),即P[0]···P[k-1];
- 此時比較第k項P[k]與P[q],如圖1所示
- 如果P[K]等於P[q],那麼很簡單跳出while迴圈;
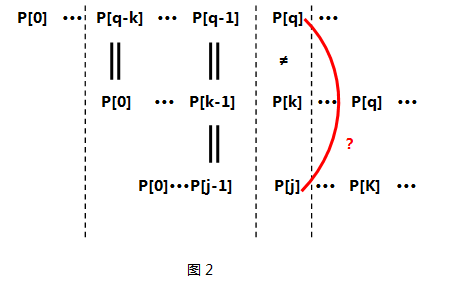
- 關鍵!關鍵有木有!關鍵如果不等呢???那麼我們應該利用已經得到的next[0]···next[k-1]來求P[0]···P[k-1]這個子串中最大相同前後綴,可能有同學要問了——為什麼要求P[0]···P[k-1]的最大相同前後綴呢???是啊!為什麼呢? 原因在於P[k]已經和P[q]失配了,而且P[q-k] ··· P[q-1]又與P[0] ···P[k-1]相同,看來P[0]···P[k-1]這麼長的子串是用不了了,那麼我要找個同樣也是P[0]打頭、P[k-1]結尾的子串即P[0]···P[j-1](j==next[k-1]),看看它的下一項P[j]是否能和P[q]匹配。如圖2所示

附程式碼:
1 #include<stdio.h> 2 #include<string.h> 3 void makeNext(const char P[],int next[]) 4 { 5 int q,k; 6 int m = strlen(P); 7 next[0] = 0; 8 for (q = 1,k = 0; q < m; ++q) 9 { 10 while(k > 0 && P[q] != P[k]) 11 k = next[k-1]; 12 if (P[q] == P[k]) 13 { 14 k++; 15 } 16 next[q] = k; 17 } 18 } 19 20 int kmp(const char T[],const char P[],int next[]) 21 { 22 int n,m; 23 int i,q; 24 n = strlen(T); 25 m = strlen(P); 26 makeNext(P,next); 27 for (i = 0,q = 0; i < n; ++i) 28 { 29 while(q > 0 && P[q] != T[i]) 30 q = next[q-1]; 31 if (P[q] == T[i]) 32 { 33 q++; 34 } 35 if (q == m) 36 { 37 printf("Pattern occurs with shift:%d\n",(i-m+1)); 38 } 39 } 40 } 41 42 int main() 43 { 44 int i; 45 int next[20]={0}; 46 char T[] = "ababxbababcadfdsss"; 47 char P[] = "abcdabd"; 48 printf("%s\n",T); 49 printf("%s\n",P ); 50 // makeNext(P,next); 51 kmp(T,P,next); 52 for (i = 0; i < strlen(P); ++i) 53 { 54 printf("%d ",next[i]); 55 } 56 printf("\n"); 57 58 return 0; 59 }
3.kmp的優化
待續。。。。
相關推薦
【經典演算法】——KMP,深入講解next陣列的求解
前言 之前對kmp演算法雖然瞭解它的原理,即求出P0···Pi的最大相同前後綴長度k;但是問題在於如何求出這個最大前後綴長度呢?我覺得網上很多帖子都說的不是很清楚,總感覺沒有把那層紙戳破,後來翻看演算法導論,32章 字串匹配雖然講到了對前字尾計算的正確性,但是大量的推理證明不大好理解,沒有與程式結合
【經典演算法】:蛇形填數,最簡單的方法了。。。
問題概述 什麼是蛇形填數,百度一下即可 解法 你能發現這裡面的數為1到 n*n; 所以寫個迴圈即可 while(count<n*n){ while(x+1&l
【經典演算法】:希爾排序的實現
希爾排序我感覺並沒有什麼用 = =因為希爾排序事實上是對插入排序的一個複雜化,在插入排序的基礎上引入了一種分組機制,所以這種排序事實上是複雜了。 並且這種排序和插入排序的實現機制非常相似,只要稍微增加
【經典演算法】:BFS與DFS
寫在最前的三點: 1、所謂圖的遍歷就是按照某種次序訪問圖的每一頂點一次僅且一次。 2、實現bfs和dfs都需要解決的一個問題就是如何儲存圖。一般有兩種方法:鄰接矩陣和鄰接表。這裡為簡單起 見,均採用鄰接矩陣儲存,說白了也就是二維陣列。 3、本文章的小測試部分的測試例項
【經典演算法】:如何判斷整數和浮點數是否相等
這個問題來自於我解決一個叫做五猴分桃的問題 其中會出現這麼一些資料 我需要在右邊第二欄資料裡面找到整數型的資料,比如說 3121這類的資料 但是我給第二欄定義的是float型的資料,如何判斷這個float型的資料是不是整數呢? 用瞭如下方法,注意看!
【經典演算法】: 羅馬數字
關於羅馬數字,一到10可以介紹給大家一個簡單的記法 I 代表 1 V 代表 5 X 代表 10 4 9 特殊記 在 V 和 X 的左邊放一個 I 代表減去 1 thus : 4 —>
【經典演算法】:關於大小寫的轉換問題
tips: 知道一點即可,所有字元都是0-255之間的值,所以大小寫的轉換隻需要對其進行數值上面的加減運算就可以了 小寫字母的值比大寫字母的值大32 展示一個程式碼: 這個就可以把a轉換為大A,
【經典演算法】:烙餅排序
原理非常簡單,看視訊即可 給一個為排序的陣列,你只能再改對該陣列做如下操作:flip(arr, i): 將陣列arr[0...i]進行逆置。如何對該陣列進行排序? 這個問題在程式設計之美一書也有提及: 星期五的晚上,一幫同事在希格瑪大廈附近的“硬碟酒吧”多喝了幾杯。程式設
【經典演算法】:愛因斯坦臺階問題
愛因斯坦臺階問題 愛因斯坦曾經提出過這樣一道有趣的數學題:有一個長階梯,若每步上2階,最後剩下1階;若每步上3階,最後剩2階;若每步上5階,最後剩下4階;若每步上6階,最後剩5階;只有每步上7階,最後剛好一階也不剩。請問該階梯至少有多少階。 解題思路 不是
【經典演算法】:把String變為double型的方法
題目 如題,假設資料為:63.2558的string型別,如何把它變為double型 處理辦法 直接細節入手,前面先找到前置位,後面找到後置位,都是一些普通的辦法,然後把它一起加起來,最後就得到
【經典演算法】:Dijskstra演算法與Floyd演算法
Dijkstra演算法利用的是一個經典的東西,叫做保持好的最短路徑,目的就是為了在尋找最短路徑的時候的保持最短化的過程 Floyd演算法利用的是一個經典的公式 D[I,J]>D[I,K] + D[K,J] 則 D[I J] = D[I K] + D[K J]
KMP匹配詳細講解+next陣列真正理解
之前轉載過一篇kuangbin大佬的kmp模板,只會用,但是不清楚原理現在看了某大佬的文章,發現講解的非常精彩,但是有一點不足就是沒講清楚KMP時間複雜度問題,但是自己的語言組織能力以及理解能力也不是很好,所以就直接copyt過來了。希望_july_v博主不介意。http:/
【演算法】KMP經典演算法,你真的懂了嗎?
有關KMP演算法的書籍、帖子、部落格鋪天蓋地,但是你真的能看懂?你知道為什麼要有next陣列,next陣列到底什麼意思,又該怎麼求next陣列,有了next陣列之後又該怎樣判斷模式串和主串是否匹配成功?本文絕對不是講解KMP演算法最細緻的一篇文章,但卻是為了解決
【免費直播課】今晚8點,深入講解服務器硬件和產品選型
公開課 服務區 公開課主題:服務器硬件架構與項目實戰【夏傑老師】 公開課背景:市面上服務器,基本只有兩類課程,要麽講系統(Windows/Linux),要麽講虛擬化(VMware/Ctrix/KVM),沒有一門課程去深入講解服務器硬件和產品選型。此次公開課帶你揭開服務器硬件面紗,並結合實戰,深入理解服
【演算法】棧,括號匹配
棧,括號匹配 import java.util.Scanner; import java.util.Stack; public class Main { public static void main(String[] args){ Stack&
【智慧演算法】粒子群演算法(Particle Swarm Optimization)超詳細解析+入門程式碼例項講解
喜歡的話可以掃碼關注我們的公眾號哦,更多精彩盡在微信公眾號【程式猿聲】 01 演算法起源 粒子群優化演算法(PSO)是一種進化計算技術(evolutionary computation),1995 年由Eberhart 博士和kennedy 博士提出,源於對鳥群捕食的行為研究 。該演算法最初是受到飛鳥叢集
【面試題】KMP演算法實現
what!? KMP演算法是幹嘛的? 我們可能都知道樸素演算法,主要是解決兩個字串的匹配問題,其實KMP演算法可以說和樸素演算法是師出同門,為什麼這麼講呢?首先我們對比一下兩個的程式碼,大家就知道怎麼回事了。 樸素演算法 int BF(const char *str1
HDU 2544 最短路【Dijkstra演算法堆優化,Vector建圖】
最短路 Time Limit: 5000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Submission(s): 55757 Accepted Submissi
【演算法】堆,最大堆(大頂堆)及最小堆(小頂堆)的實現
此坑待埋。 下面來說一說具體演算法。 堆排序解釋第一篇(描述不太清楚) 1.堆 堆實際上是一棵完全二叉樹,其任何一非葉節點滿足性質: Key[i]<=key[2i+1]&&Key[i]<=key[2i+2
【模式匹配】KMP演算法的來龍去脈
1. 引言 字串匹配是極為常見的一種模式匹配。簡單地說,就是判斷主串\(T\)中是否出現該模式串\(P\),即\(P\)為\(T\)的子串。特別地,定義主串為\(T[0 \dots n-1]\),模式串為\(P[0 \dots p-1]\),則主串與模式串的長度各為\(n\)與\(p\)。 暴力匹配 暴力匹配
