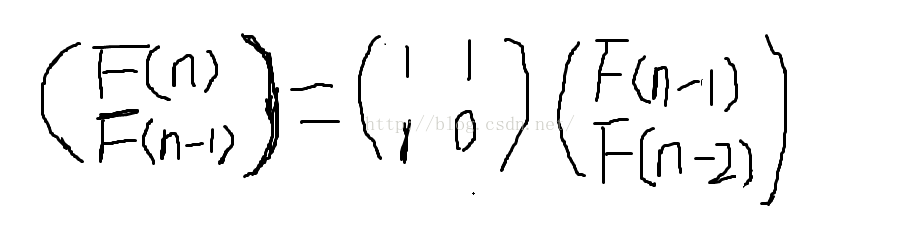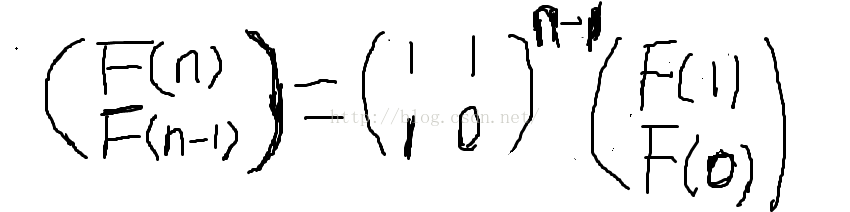斐波那契數列的第 n 項 mod 1000000007(矩陣乘法)
阿新 • • 發佈:2018-12-24
矩陣快速冪:
F(0) = 0
F(1) = 1
F(n) = F(n - 1) + F(n - 2) (n >= 2)
(1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, ...)
給出n,求F(n),由於結果很大,輸出F(n) % 1000000007的結果即可。
引例 :求斐波那契數列的第 n 項 mod
1000000007 的值, n <= 10 18 。
分析 :斐波那契數列的遞推式為 f(n) = f(n-1)+f(n-2) ,直接迴圈求出 f(n) 的時間複雜度是 O(n) ,對於題目中的資料範圍顯然無法承受。很明顯我們需要對數級別的演算法。
即:
所以我們只要不斷地乘以上面式子中的第二個矩陣(也就是第二個矩陣的冪)就能夠不斷遞推得到 f(n) 。但是這樣於解題沒有絲毫益處,反而使得常數變得更大(矩陣乘法的複雜度為立方級別)。所以我們就要利用矩陣乘法的一條重要性質:結合律。即矩陣 (A*B)*C = A*(B*C) ,證明過程可參見 2008 年國家集訓隊俞華程的論文。
有了結合律我們就可以用快速冪計算矩陣的冪,問題的複雜度順利降到了 O(logn)。
程式碼:
#include<iostream> #include<memory.h> #include<cstdlib> #include<cstdio> #include<cmath> #include<cstring> #include<string> #include<cstdlib> #include<iomanip> #include<vector> #include<list> #include<map> #include<algorithm> typedef long long LL; const LL maxn=1000+10; const LL mod=1000000007; const int N=2; using namespace std; struct Matrix { LL m[N][N]; }; Matrix A= { 1,1, 1,0 }; Matrix I= { 1,0, 0,1 }; Matrix multi(Matrix a,Matrix b) { Matrix c; for(int i=0;i<N;i++) { for(int j=0;j<N;j++) { c.m[i][j]=0; for(int k=0;k<N;k++) c.m[i][j]+=a.m[i][k]*b.m[k][j]%mod; c.m[i][j]%=mod; } } return c; } Matrix power(Matrix A,int k) { Matrix ans=I,p=A; while(k) { if(k&1) { ans=multi(ans,p); k--; } k>>=1; p=multi(p,p); } return ans; } int main() { int n; while(~scanf("%d",&n)) { Matrix ans =power(A,n-1); printf("%lld\n",ans,m[0][0]); } return 0; }