【codeforces 732E】【貪心 map亂搞】
描述:
E. Sockets time limit per test 2 seconds memory limit per test 256 megabytes input standard input output standard outputThe ICM ACPC World Finals is coming! Unfortunately, the organizers of the competition were so busy preparing tasks that totally missed an important technical point — the organization of electricity supplement for all the participants workstations.
There are n computers for participants, the i-th
of which has power equal to positive integer pi.
At the same time there are m sockets available, the j-th
of which has power euqal to positive integer sj.
It is possible to connect the i-th computer to the j-th
socket if and only if their powers are the same: p
In order to fix the situation professor Puch Williams urgently ordered a wagon of adapters — power splitters. Each adapter has one plug and one socket with a voltage divider between them. After plugging an adapter to a socket with
power x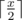 ,
it means that it is equal to the socket's power divided by two with rounding up, for example
,
it means that it is equal to the socket's power divided by two with rounding up, for example 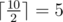 and
and 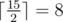 .
.
Each adapter can be used only once. It is possible to connect several adapters in a chain plugging the first to a socket. For example, if two adapters are plugged one after enother to a socket with power 10, it becomes possible to connect one computer with power 3 to this socket.
The organizers should install adapters so that it will be possible to supply with electricity the maximum number of computers c at the same time. If there are several possible connection configurations, they want to find the one that uses the minimum number of adapters uto connect c computers.
Help organizers calculate the maximum number of connected computers c and the minimum number of adapters u needed for this.
The wagon of adapters contains enough of them to do the task. It is guaranteed that it's possible to connect at least one computer.
InputThe first line contains two integers n and m (1 ≤ n, m ≤ 200 000) — the number of computers and the number of sockets.
The second line contains n integers p1, p2, ..., pn (1 ≤ pi ≤ 109) — the powers of the computers.
The third line contains m integers s1, s2, ..., sm (1 ≤ si ≤ 109) — the power of the sockets.
OutputIn the first line print two numbers c and u — the maximum number of computers which can at the same time be connected to electricity and the minimum number of adapters needed to connect c computers.
In the second line print m integers a1, a2, ..., am (0 ≤ ai ≤ 109), where ai equals the number of adapters orginizers need to plug into thei-th socket. The sum of all ai should be equal to u.
In third line print n integers b1, b2, ..., bn (0 ≤ bi ≤ m), where the bj-th equals the number of the socket which the j-th computer should be connected to. bj = 0 means that the j-th computer should not be connected to any socket. All bj that are different from 0 should be distinct. The power of the j-th computer should be equal to the power of the socket bj after plugging in abj adapters. The number of non-zero bj should be equal to c.
If there are multiple answers, print any of them.
Examples input2 2
1 1
2 2
output
2 2
1 1
1 2
input
2 1
2 100
99
output
1 6
6
1 0
題意:
給出n個電腦,m個電源,電腦有一個值ai,電源有一個值bi,電腦和電源能夠配對當且僅當ai=bi。有無窮多個介面卡,每對電源用一個介面卡bi就減少一半(向上取整)。一個電源可以用很多次介面卡。求最多配對多少電腦和電源,以及在最多配對下用的最少的介面卡。還要輸出方案。
思路:
將電源按照從小到大依次嘗試和電腦配對,如果能夠配對成功就配對。可以反證,假設按照這個順序配對會使得配對數減少,也就是說有一個比他大的電源本應該和這個電腦相配。因為這兩個電源都匹配到了這個電腦,所以當前列舉的電源往下能夠匹配的電腦也能被那個比他大的電源匹配掉。
那麼這樣貪心會不會使得介面卡數量不是最佳呢?容易證明是最少的。因為如果有多個值一樣的電腦需要匹配當然優選電源小的來匹配(等值的電腦順序任意),如果本來就只能配對這一個電腦,顯然用較小的電源是最優的。
程式碼:
#include <bits/stdc++.h>
using namespace std;
#define rep(i,k,n) for(int i=k;i<=n;i++)
template<class T> T sqr(T x){ return x * x; }
template<class T> T gcd(T a, T b){ return b ? gcd(b, a%b) : a; }
template<class T> void read(T&num) {
char CH; bool F=false;
for(CH=getchar();CH<'0'||CH>'9';F= CH=='-',CH=getchar());
for(num=0;CH>='0'&&CH<='9';num=num*10+CH-'0',CH=getchar());
F && (num=-num);
}
const int N=2e5+10;
struct node{
int num, id;
node(){}
node(int nu, int i): num(nu), id(i) {}
bool operator < (const node& tmp)const{
if(num != tmp.num)return num < tmp.num;
return id < tmp.id;
}
}p[N], s[N];
std::map<int, int> mp;//計算機值出現的次數
int a[N], b[N], c, u;
int main(){
int n, m;
read(n), read(m);
rep(i, 1, n){
read(p[i].num);
p[i].id = i;
mp[p[i].num]++;
}
sort(p + 1, p + n + 1);
rep(i, 1, m){
read(s[i].num);
s[i].id = i;
}
sort(s + 1, s + m + 1);
rep(i, 1, m){
rep(j, 0, 30){
if(mp.count(s[i].num)){//發現可能匹配
int t = lower_bound(p + 1, p + n + 1, node(s[i].num, 0)) - p +mp[s[i].num] - 1;
//找到位置(由於有可能有多個相同的值,這裡先從最後一個開始往前推)
if(p[t].num == s[i].num && !b[p[t].id]){//
b[p[t].id] = s[i].id; //電腦匹配到的socket
mp[s[i].num]--;//數量-1
a[s[i].id] = j; //對應的socket需要多少adapters
u += j;
c++;
break;
}
}
s[i].num = (s[i].num + 1) >> 1;
}
}
printf("%d %d\n", c, u);
rep(i, 1, m)printf("%d%c", a[i], i == m ? '\n':' ');
rep(i, 1, n)printf("%d%c", b[i], i == n ? '\n':' ');
return 0;
}