線段樹區間查詢
阿新 • • 發佈:2018-12-24
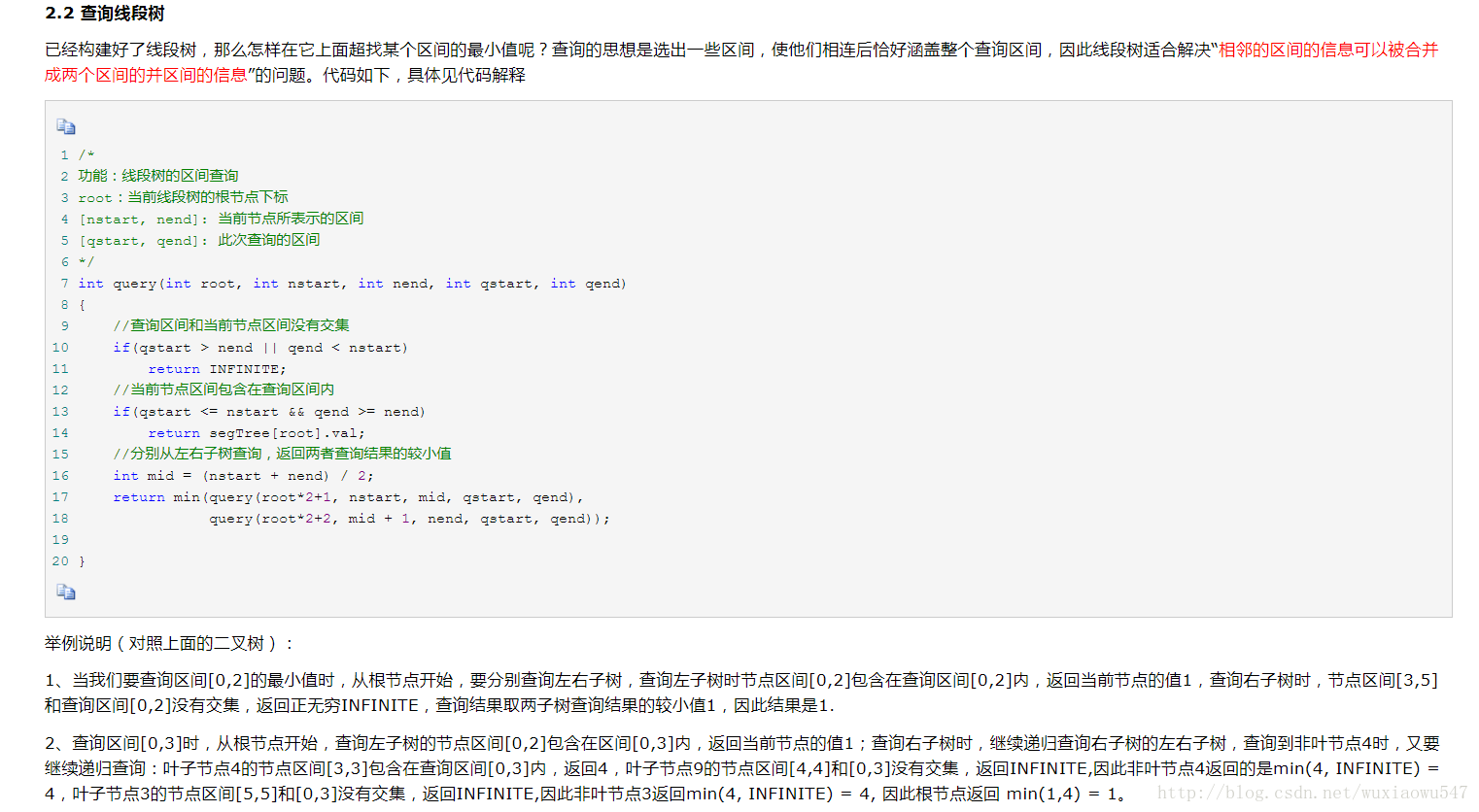
給定一個區間,判斷線段樹中的區間在該區間內的最小權值;
查詢的思想是選出一些區間,使他們相連後恰好涵蓋整個查詢區間,因此線段樹適合解決“相鄰的區間的資訊可以被合併成兩個區間的並區間的資訊”的問題。
這個部落格介紹的很好,尤其是下面的舉例非常的詳細。
[https://www.cnblogs.com/TenosDoIt/p/3453089.html#g]
程式碼:
#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cmath>
#define MAXN 1000