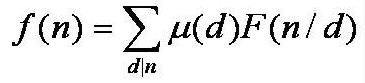莫比烏斯函式

這裡簡述一下莫比烏斯函式：

若d=1 那麼μ(d)=1
若d=p1p2…pr （r個不同質數，且次數都為一）μ(d)=(-1)^r
其餘 μ(d)=0

即μ[i]=1表示i是偶數個不同素因子的乘積，μ[i]=-1表示i是奇數個不同素因子的乘積，μ[i]=0表示其他（即如果有相同素因子就是0）

而i==1時，規定μ[1] = 1。

莫比烏斯反演的性質

性質一：（莫比烏斯反演公式）

f(n)=∑(d|n)μ(d)F(n/d)

性質二：μ(n)是積性函式

性質三：設f是算術函式，它的和函式F(n)=∑(d|n)f(d)是積性函式，那麼f也是積性函式。

HDU - 1695 - GCD

題目傳送：GCD

題意：求[1,n],[1,m]中gcd為k的兩個數的對數

思路：這裡可以轉化一下，也就是[1,n/k],[1,m/k]之間互質的數的個數，模板題

設F(n)為公約數為n的組數個數
f(n)為最大公約數為n的組數個數

F(n)=∑(n|d)f(d)

所以有：

f(n)=∑(n|d)μ(d/n)F(d)

不過這裡需要注意去重，即去掉重複的那一部分的一半即可

AC程式碼：

#include <map>
#include <set>
#include <list>
#include <cmath>
 

#include <deque>
#include <queue>
#include <stack>
#include <bitset>
#include <cctype>
#include <cstdio>
#include <string>
#include <vector>
#include <complex>
#include <cstdlib>
#include <cstring>
#include <fstream>
#include <sstream>
 

#include <utility>
#include <iostream>
#include <algorithm>
#include <functional>
#define LL long long
#define INF 0x7fffffff
using namespace std;

const int maxn = 1000005;

bool vis[maxn];
int prime[maxn];
int mu[maxn];
int tot;

void init() {
    memset(vis, 0, sizeof(vis));
    mu[1] = 1;
    tot = 0;
    for(int i = 2; i < maxn; i ++) {
        if(!vis[i]) {
            prime[tot ++] = i;
            mu[i] = -1;
        }
        for(int j = 0; j < tot; j ++) {
            if(i * prime[j] >= maxn) break;
            vis[i * prime[j]] = true;
            if(i % prime[j] == 0) {
                mu[i * prime[j]] = 0;
                break;
            }
            else {
                mu[i * prime[j]] = -mu[i];
            }
        }
    }
}

int main() {

    init();

    int T;
    int a, b, c, d, k;

    scanf("%d", &T);
    for(int cas = 1; cas <= T; cas ++) {
        scanf("%d %d %d %d %d", &a, &b, &c, &d, &k);
        if(k == 0) {
            printf("Case %d: 0\n", cas);
            continue;
        }
        b /= k;
        d /= k;
        if(b > d) swap(b, d);
        LL ans = 0;
        for(int i = 1; i <= b; i ++) {
            ans += (LL)mu[i] * (b / i) * (d / i);
        }
        LL t = 0;
        for(int i = 1; i <= b; i ++) {
            t += (LL)mu[i] * (b / i) * (b / i);
        }

        ans -= t / 2;
        printf("Case %d: %I64d\n", cas, ans);

    }

    return 0;
}