前言
Kruskal是在一個圖（圖論）中生成最小生成樹的演算法之一。（另外還有Prim演算法，之後會涉及到）這就牽扯到了最小生成樹的概念，其實就是總權值最小的一個連通無迴路的子圖。（結合下文的示意圖不難理解）這裡的程式碼並沒有用圖的儲存結構（如：矩陣，鄰接連結串列等）來處理和運用這個演算法，而是最簡單的三元組輸入，這樣會使得這個過程簡化很多，至於圖的儲存方式，在之後總結圖資料結構的時候會具體討論。

Kruskal演算法的思想與過程
（1）思想：其實這個演算法的本質還是一個貪心演算法的過程。其實我們可以這樣想，一個圖中，我們要想讓生成的子圖（更確切的說是樹）總權值最小，那麼只要依次選擇圖中權值最小的邊、權值次小的邊、……，這樣自然就保證了生成的圖總權值最小。但是別忘了一點，我們要求的生成的子圖還得是一棵樹（樹的定義：一個連通無迴路的圖），這就帶來了一個問題，我們在權值從小到大選擇邊的時候，可能會使生成的子圖產生了迴路，這就不符合概念了，所以我們不僅需要權值從小到大選擇邊還應該保證這些邊組成的子圖構不成迴路

過程（標準定義）：
任給一個有n個頂點的連通網路N = {V, E}，首先構造一個由這n個頂點組成、不含任何邊的圖T = {V, 空集}，其中每個頂點自成一個連通分量。不斷從E中取出權值最小的一條邊（若有多條，任取其一），若該邊的兩個端點來自不同的連通分量，則將此邊加入T中。如此重複，直到所有頂點在同一個連通分量上為止。

為何用並查集與最小堆實現Kruskal演算法？

這個問題最根本的解答在上面Kruskal演算法的實現過程當中，過程中涉及到兩個重要的步驟：

(1)每次取得權值最小的邊
(2)判斷加入的邊的兩個端點是否來自同一連通分量（實質就是保證加入邊後不會產生迴路）

而最小堆可以實現每次取得一組資料中關鍵碼（這裡可以代表權值大小）最小的資料；並查集可以將不同的集合（這裡可以代表點集合）Union起來並且可以判斷不同集合是否有交集（這裡可以判斷兩個點是否同屬於一個集合，進而判斷加入邊後是否會出現迴路！）。沒錯！這簡直就是Kruskal演算法實現的標配，下面Kruskal演算法的實現過程圖也體現了這一點！（注：之前的博文對最小堆和並查集都有總結，對這兩個資料結構概念不清的話可以看看）
Kruskal演算法生成最小生成樹的一個例項：
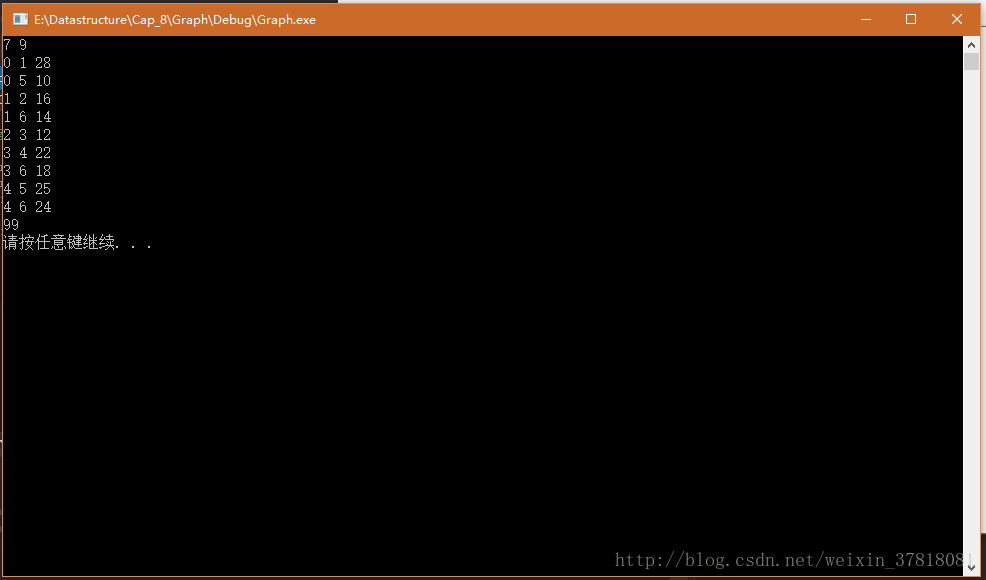
程式輸入資料（三元組格式）：

7 9 //圖的頂點數量、圖的邊的數量
0 1 28 //下面每行都儲存了一個邊的資訊
0 5 10 //依次表示：邊的端點1、邊的端點2、邊的權值
1 2 16
1 6 14
2 3 12
3 4 22
3 6 18
4 5 25
4 6 24
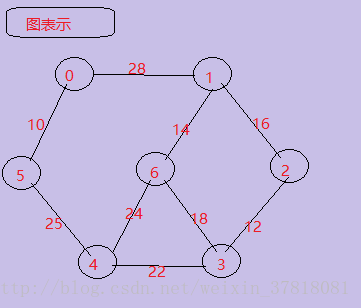
圖表示：

程式碼實現過程中結構注意點！
（1）對邊結構體的構造：

這裡必須對此結構變數的大於、大於等於、小於運算子做過載（只通過邊的權值比較即可），應為在最小堆中會直接對此變數進行比較！

（2）Kruskal演算法實現函式：

尤其注意的應該是並查集建立的時候，其建構函式為何傳遞了頂點數量多1，否則這會導致一個嚴重的錯誤（或者說是隱患）！下面會通過另一個文章著重解釋。

（3）關於輸出：

這裡只是對最小生成樹的總權重這個指標進行了輸出，其他的指標都可以通過那個儲存最小生成樹的所有邊的全域性陣列得到。

Kruskal.cpp程式碼

/*
*運用並查集及最小堆實現Kruskal演算法
*/
#include "UFSets.h"
#include "heap.h"
using namespace std;

struct WEDGE {                      //權重邊結構定義
    int vertex1, vertex2;           //決定邊的兩個頂點
    int weights;                    //邊的權重
                                    //建構函式
    WEDGE(int v1 = -1, int v2 = -1, int w = 0) {
        vertex1 = v1; 
        vertex2 = v2;
        weights = w;
    }
    bool operator >(WEDGE& WE);     //過載邊的大於比較
    bool operator <(WEDGE& WE);     //過載邊的小於比較
    bool operator >=(WEDGE& WE);    //過載大於等於比較
};
WEDGE minTreeEdges[20];             //儲存最小生成樹的邊集

void Kruskal(WEDGE* we, int edg_amou, int vex_amou);

int main()
{
    int vertexsAmount{ 0 }, edgesAmount{ 0 };   //輸入的點數與邊數      
    WEDGE wedge[20];                            //初始化20條邊   
    cin >> vertexsAmount >> edgesAmount;
    for (int i = 0; i < edgesAmount; i ++) {    //迴圈輸入邊的頂點及權重
        cin >> wedge[i].vertex1 >> wedge[i].vertex2
            >> wedge[i].weights;
    }

    Kruskal(wedge, edgesAmount, vertexsAmount);

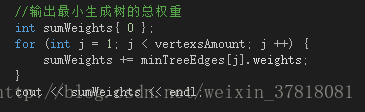
    //輸出最小生成樹的總權重
    int sumWeights{ 0 };
    for (int j = 1; j < vertexsAmount; j ++) {
        sumWeights += minTreeEdges[j].weights;
    }
    cout << sumWeights << endl;

    system("pause");
    return 0;
}

void Kruskal(WEDGE* we, int edg_amou, int vex_amou) {
    //Kruskal演算法實現函式，引數分別是：一組邊集合、邊數、頂點數
    MinHeap<WEDGE> minheap(we, edg_amou);       //建立最小堆
    UFSets uf_set(vex_amou + 1);                //建立並查集
    WEDGE edge;
    int vex_1{ 0 }, vex_2{ 0 };
    int count{ 1 };                             //最小生成樹加入邊數計數
    while (count < vex_amou){                   //選入總邊數-1條邊即可
        minheap.removeMin(edge);                //刪除並返回堆頂元素
        vex_1 = uf_set.Find(edge.vertex1);
        vex_2 = uf_set.Find(edge.vertex2);
        if (vex_1 != vex_2) {                   //兩個頂點不在同一連通分量中
            minTreeEdges[count] = edge;         //選入
            uf_set.Union(vex_1, vex_2);         //將兩個頂點連通
            count++;
        }
    }
}

//過載運算子定義
bool WEDGE::operator >(WEDGE& WE) {
    if (weights > WE.weights) {
        return true;
    }
    else {
        return false;
    }
}

bool WEDGE::operator<(WEDGE& WE) {
    if (weights < WE.weights) {
        return true;
    }
    else {
        return false;
    }
}

bool WEDGE::operator>=(WEDGE& WE) {
    if (weights >= WE.weights) {
        return true;
    }
    else {
        return false;
    }
}

這個檔案中程式碼的執行需要依靠兩個資料結構的標頭檔案——最小堆和並查集.h。這裡就不在貼出來了，需要的話可以在文章末的連結下載，也可以看之前對這兩個資料結構總結時候所貼的程式碼。下面用這段程式碼測試一下我們上面的例項！

嗯，他表現的不錯，在我們的過程圖中，最終的權值和：10+12+14+16+22+25 = 99。

另類的測試！！！
不過這只是組測試資料，我們應該再找一組程式完全陌生的資料試試，看下面的題目：（題目是在網站中摘下來的~）

資料結構實驗之圖論六：村村通公路
Time Limit : 1000MS Memory Limit : 65536KB
Submit Statistic
Problem Description
當前農村公路建設正如火如荼的展開，某鄉鎮政府決定實現村村通公路，工程師現有各個村落之間的原始道路統計資料表，
表中列出了各村之間可以建設公路的若干條道路的成本，你的任務是根據給出的資料表，求使得每個村都有公路連通所需要的最低成本。
Input
連續多組資料輸入，每組資料包括村落數目N(N <= 1000)和可供選擇的道路數目M(M <= 3000)，隨後M行對應M條道路，
每行給出3個正整數，分別是該條道路直接連通的兩個村莊的編號和修建該道路的預算成本，村莊從1～N編號。
Output
輸出使每個村莊都有公路連通所需要的最低成本，如果輸入資料不能使所有村莊暢通，則輸出 - 1，表示有些村莊之間沒有路連通。
Example Input
5 8
1 2 12
1 3 9
1 4 11
1 5 3
3 2 6
2 4 9
3 4 4
5 4 6
Example Output
19
Author
xam
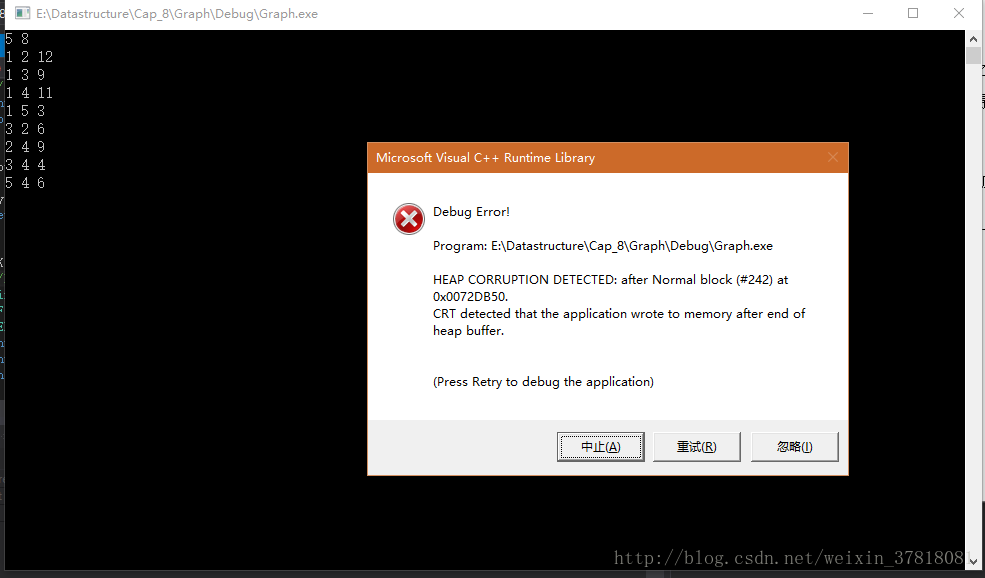
這是一個典型的應用題，看看下面的測試結果！

Oh! No!問題似乎很嚴重！程式崩潰了！這是我們的程式有問題嗎？還是其他的bug？也許不是，你可以看看這兩組輸入資料的微妙差別，也許會受到啟發！（其實上文中我已經做了提示）我保證這個Kruskal演算法的實現是沒有問題的，下篇博文會揭開這一隱患的謎底。