連結：戳這裡

D. Puzzles time limit per test1 second memory limit per test256 megabytes inputstandard input outputstandard output Barney lives in country USC (United States of Charzeh). USC has n cities numbered from 1 through n and n - 1 roads between them. Cities and roads of USC form a rooted tree (Barney's not sure why it is rooted). Root of the tree is the city number 1. Thus if one will start his journey from city 1, he can visit any city he wants by following roads.
Some girl has stolen Barney's heart, and Barney wants to find her. He starts looking for in the root of the tree and (since he is Barney Stinson not a random guy), he uses a random DFS to search in the cities. A pseudo code of this algorithm is as follows:


let starting_time be an array of length n
current_time = 0
dfs(v):
current_time = current_time + 1
starting_time[v] = current_time
shuffle children[v] randomly (each permutation with equal possibility)
// children[v] is vector of children cities of city v
for u in children[v]:
dfs(u)
As told before, Barney will start his journey in the root of the tree (equivalent to call dfs(1)).

Now Barney needs to pack a backpack and so he wants to know more about his upcoming journey: for every city i, Barney wants to know the expected value of starting_time[i]. He's a friend of Jon Snow and knows nothing, that's why he asked for your help.

Input
The first line of input contains a single integer n (1 ≤ n ≤ 105) — the number of cities in USC.

The second line contains n - 1 integers p2, p3, ..., pn (1 ≤ pi < i), where pi is the number of the parent city of city number i in the tree, meaning there is a road between cities numbered pi and i in USC.

Output
In the first and only line of output print n numbers, where i-th number is the expected value of starting_time[i].

Your answer for each city will be considered correct if its absolute or relative error does not exceed 10 - 6.

Examples
input
7
1 2 1 1 4 4
output
1.0 4.0 5.0 3.5 4.5 5.0 5.0 
input
12
1 1 2 2 4 4 3 3 1 10 8
output
1.0 5.0 5.5 6.5 7.5 8.0 8.0 7.0 7.5 6.5 7.5 8.0 

題意：

一個樹，dfs遍歷子樹的順序是隨機的。所對應的子樹的dfs序也會不同。輸出每個節點的dfs序的期望

思路：

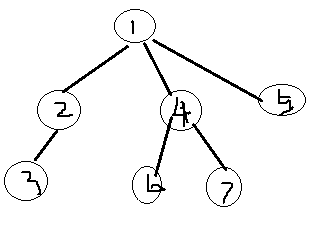
分析一顆子樹：

當前已知節點1的期望為1.0 ->anw[1]=1.0

需要通過節點1遞推出節點2、4、5的期望值

1的兒子分別是2、4、5，那麼dfs序所有可能的排列是6種：

1：1-2-4-5  （2、4、5節點的兒子沒有寫出）

2：1-2-5-4

3：1-4-2-5

4：1-4-5-2

5：1-5-2-4

6：1-5-4-2

計算節點2的期望值得時候，當節點2的前面已經排列了num個點，那麼節點2的dfs序就要增加num

所以anw[2]的計算分為兩部分，第一部分是：anw[2]=anw[1]+1  （節點1通過1步直接到達兒子2、4、5）

第二部分是：當節點1到達節點2的時候貢獻是0，種類分別對應(1、2)

      當先到達節點4後到節點2的時候貢獻(size(4)+size(4)+szie(5))，種類分別對應(3、4)

      當先到達節點5後到節點2的時候貢獻(size(5)+size(5)+size(4))，種類分別對應(5、6)

而所有的排列對於的概率都是1/6，所以第二部分的貢獻就是（0+size(4)*3+size(5)*3）/6 = (size(4)+size(5))/2

仔細推理幾顆子樹之後：發現anw[v]=anw[u]+1.0+(sz[u]-sz[v]-1)/2.0。

anw[u]+1.0對應第一部分  (sz[u]-sz[v]-1)/2.0 表示的是當前能排在節點v前面的u的兒子的總數  *  0.5

對比1-6的6種排列，任意兒子a、b  ，滿足a在b前面的概率是0.5  

程式碼：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<string>
#include<vector>
#include <ctime>
#include<queue>
#include<set>
#include<map>
#include<stack>
#include<iomanip>
#include<cmath>
#define mst(ss,b) memset((ss),(b),sizeof(ss))
#define maxn 0x3f3f3f3f
#define MAX 1000100
///#pragma comment(linker, "/STACK:102400000,102400000")
typedef long long ll;
typedef unsigned long long ull;
#define INF (1ll<<60)-1
using namespace std;
int n;
struct edge{
    int v,next;
}e[500100];
int head[100100],tot=0;
void Add(int u,int v){
    e[tot].v=v;
    e[tot].next=head[u];
    head[u]=tot++;
}
int sz[100100];
void DFS(int u,int fa){
    sz[u]=1;
    for(int i=head[u];i!=-1;i=e[i].next){
        int v=e[i].v;
        if(v==fa) continue;
        DFS(v,u);
        sz[u]+=sz[v];
    }
}
double anw[100100];
void DFS1(int u,int fa){
    for(int i=head[u];i!=-1;i=e[i].next){
        int v=e[i].v;
        if(v==fa) continue;
        anw[v]=anw[u]+1.0+(sz[u]-sz[v]-1)*1.0/2.0;
        DFS1(v,u);
    }
}
int main(){
    mst(head,-1);
    scanf("%d",&n);
    for(int i=2;i<=n;i++){
        int x;
        scanf("%d",&x);
        Add(x,i);
        Add(i,x);
    }
    DFS(1,0);
    anw[1]=1.0;
    DFS1(1,0);
    for(int i=1;i<=n;i++) printf("%.2f ",anw[i]);
    return 0;
}