1922: [Sdoi2010]大陸爭霸
Time Limit: 10 Sec Memory Limit: 64 MB
Submit: 1154 Solved: 478
[Submit][Status][Discuss]

Description
在一個遙遠的世界裡有兩個國家：位於大陸西端的傑森國和位於大陸東端的 克里斯國。兩個國家的人民分別信仰兩個對立的神：傑森國信仰象徵黑暗和毀滅 的神曾·布拉澤，而克里斯國信仰象徵光明和永恆的神斯普林·布拉澤。 幻想歷 8012年 1月，傑森國正式宣佈曾·布拉澤是他們唯一信仰的神，同 時開始迫害在傑森國的信仰斯普林·布拉澤的克里斯國教徒。 幻想歷 8012年 3月2日，位於傑森國東部小鎮神諭鎮的克里斯國教徒發動 起義。 幻想歷 8012年 3月7日，神諭鎮的起義被傑森國大軍以殘酷手段鎮壓。 幻想歷 8012年 3月8日，克里斯國對傑森國宣戰。由數十萬大軍組成的克 里斯軍團開至兩國邊境，與傑森軍團對峙。 幻想歷 8012年 4月，克里斯軍團攻破傑森軍團防線進入神諭鎮，該鎮倖存 的克里斯國教徒得到解放。 戰爭隨後進入膠著狀態，曠日持久。戰況慘烈，一時間槍林彈雨，硝煙瀰漫， 民不聊生。 幻想歷 8012年 5月12日深夜，斯普林·布拉澤降下神諭：“Trust me, earn eternal life.”克里斯軍團士氣大增。作為克里斯軍團的主帥，你決定利用這一機 會發動奇襲，一舉擊敗傑森國。具體地說，傑森國有 N 個城市，由 M條單向道 路連線。神諭鎮是城市 1而傑森國的首都是城市 N。你只需摧毀位於傑森國首都 的曾·布拉澤大神殿，傑森國的信仰，軍隊還有一切就都會土崩瓦解，灰飛煙滅。 為了儘量減小己方的消耗，你決定使用自爆機器人完成這一任務。唯一的困 難是，傑森國的一部分城市有結界保護，不破壞掉結界就無法進入城市。而每個 城市的結界都是由分佈在其他城市中的一些結界發生器維持的，如果想進入某個 城市，你就必須破壞掉維持這個城市結界的所有結界發生器。 現在你有無限多的自爆機器人，一旦進入了某個城市，自爆機器人可以瞬間 引爆，破壞一個目標（結界發生器，或是傑森國大神殿），當然機器人本身也會 一起被破壞。你需要知道：摧毀傑森國所需的最短時間。

Input
第一行兩個正整數 N, M。 接下來 M行，每行三個正整數 ui, vi, wi，表示有一條從城市ui到城市 vi的單 向道路，自爆機器人通過這條道路需要 wi的時間。 之後 N 行，每行描述一個城市。首先是一個正整數 li，維持這個城市結界所 使用的結界發生器數目。之後li個1~N 之間的城市編號，表示每個結界發生器的 位置。如果 Li = 0，則說明該城市沒有結界保護，保證L1 = 0 。

Output
僅包含一個正整數 ，擊敗傑森國所需的最短時間。

Sample Input
6 6
1 2 1
1 4 3
2 3 1
2 5 2
4 6 2
5 3 2
0
0
0
1 3
0
2 3 5

Sample Output
5

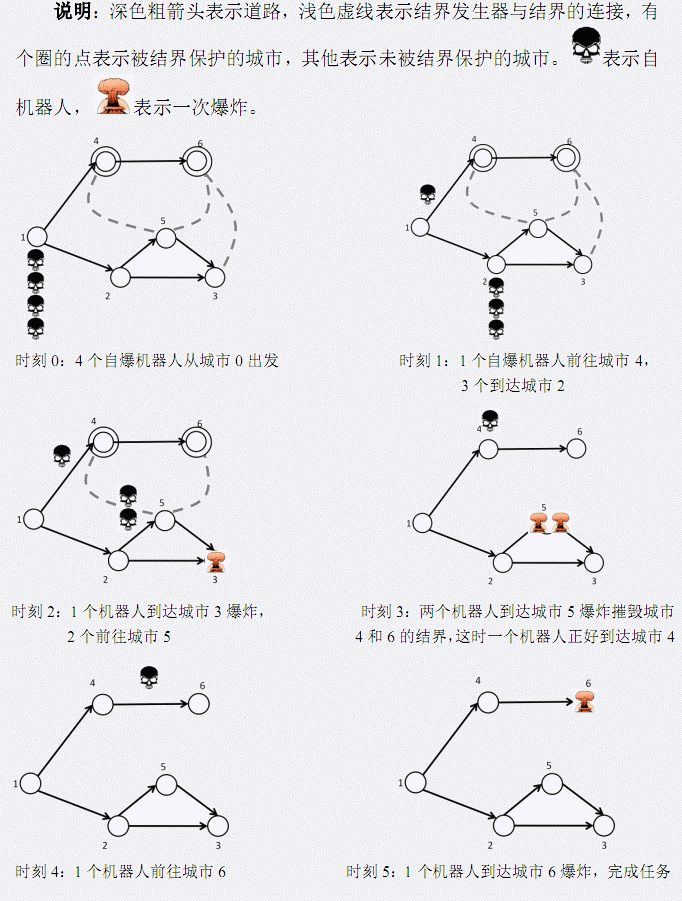
HINT
對於 20%的資料，滿足 N≤15，M≤50；
對於 50%的資料，滿足 N≤500，M≤6,000；
對於 100%的資料，滿足 N≤3,000，M≤70,000，1≤wi≤108
。
輸入資料保證一定有解，且不會存在維持某個城市結界的結界發生器在這個
城市內部。
連線兩個城市的道路可能不止一條， 也可能存在一個城市自己到自己的道路。

Source
第一輪Day1

心路歷程:
首先看題，看資料範圍前，以為是網路流，看到資料範圍打消念頭，感覺像是最短路，但需要很多限制；
胡搞了個spfa，加了點限制，發現有問題，微機課下了回班。
想了一節課，發現只需要開兩個dis陣列，分別記錄能進入這個點，以及最短進入這個點的時間…..
於是修改了一下，1A9WA…..
繼續改，發現spfa寫起來好像不是很方便，換dijskra吧，然後繼續搞，再交3A7WA….
當時的心理是崩潰的，用了STL後出現莫名的錯誤，就把自己的struct改成了pair搞了搞，4A6W….woc！
仔細讀題，MD……看錯l的意義了….改之，A了…..真蛋疼….
屈辱的做題過程…..

題解：

dis1【】記錄 最短路，dis2【】記錄最早能進這個點，即保護這個點的所有點都被炸 於是每個點的最短
即max（dis1【】，dis2【】）； 記錄保護的城市個數，每次把 可以到達的點仍到堆中，或者是保護的點扔到堆中
扔到堆中時，需要滿足被0個城市保護（無保護，或保護的全被炸了）

code：
很多除錯的痕跡，還騙了組資料。。。TAT

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
#define p pair<int,int>
int read()
{
    int x=0,f=1; char ch=getchar();
    while (ch<'0' || ch>'9') {if (ch=='-') f=-1; ch=getchar();}
    while (ch>='0' && ch<='9') {x=x*10+ch-'0'; ch=getchar();}
    return x*f;
}
#define maxn 3010
#define maxm 70010
int n,m;
struct data{int to,next,w;}edge[maxm];
int l[maxn][maxn],lt[maxn],ll[maxn];
int head[maxn],cnt;
int S,T;

void add(int u,int v,int w)
{
    cnt++;
    edge[cnt].next=head[u];  head[u]=cnt;
    edge[cnt].to=v; edge[cnt].w=w;
}

int dis1[maxn],dis2[maxn];
bool visit[maxn];
priority_queue<p,vector<p>,greater<p> >q;
void dijkstra()
{
    memset(dis1,0x3f,sizeof(dis1));
    q.push(make_pair(0,S));  dis1[S]=0;
    while (!q.empty())
        {
            int now=q.top().second; q.pop(); 
            if(visit[now]) continue; visit[now]=1;
            //printf("%d\n",now);
            int dis=max(dis1[now],dis2[now]);
            for (int i=head[now]; i; i=edge[i].next)    
                if (dis+edge[i].w<dis1[edge[i].to])
                    {
                        dis1[edge[i].to]=dis+edge[i].w;
                        int tmp=max(dis1[edge[i].to],dis2[edge[i].to]);
                        if(!ll[edge[i].to]) q.push(make_pair(tmp,edge[i].to));
                    }
            //printf("%d\n",lt[now]);
            for (int i=1; i<=lt[now]; i++)
                {
                    int noww=l[now][i]; ll[noww]--;
                    dis2[noww]=max(dis2[noww],dis);
                    if (!ll[noww]) q.push(make_pair(max(dis1[noww],dis2[noww]),noww));
                }
        }
}

int main()
{
    n=read(),m=read();
//    if (n==3000) {printf("97686");return 0;}
    for (int i=1; i<=m; i++)
        {
            int u=read(),v=read(),w=read();
            if (u!=v) add(u,v,w);
        }
    for (int i=1; i<=n; i++)
        {
            ll[i]=read();
            for (int j=1; j<=ll[i]; j++)
                {
                    int x=read();
                    l[x][++lt[x]]=i;
                }
        }
    S=1;T=n;
    dijkstra();
//  for (int i=1; i<=n; i++)
//      printf("%d %d\n",dis1[i],dis2[i]);
    printf("%d\n",max(dis1[T],dis2[T]));
    return 0;
}