1、基本概念

二叉搜尋樹：又稱二叉排序樹，它或者是一棵空樹，或者是具有以下性質的二叉樹

• 若它的左子樹不為空，則左子樹上所有節點的值都小於根節點的值
• 若它的右子樹不為空，則右子樹上所有節點的值都大於根節點的值
• 它的左右子樹也分別為二叉搜尋樹
• 沒有鍵值相等的節點

特點：

• 二叉搜尋樹的最左子樹存放最小的值，最右子樹存放最大的值；
• 二叉搜尋樹如果按中序遍歷的話，得到的數列是有序的；

2、基本操作分析

【普通版】

查詢：

根據二叉搜尋樹的特點，我們要查詢一個數，可以進行以下操作：

1. 從根節點開始遍歷，如果為空樹，返回false;如果不為空樹，則令要查詢的值與根值進行比較；
2. 如果等於根值，則返回true;
3. 如果大於根值，進入該樹的右子樹；
4. 如果小於根值，進入該樹的左子樹；
5. 重複以上步驟，直到不滿足迴圈條件；

插入：

這個也是依據二叉搜尋樹的特性來看的，與查詢很相似

• 判斷是否為空樹，若為空，則直接給該樹的根節點賦值，並返回true;
• 若不為空，則開始查詢要插入元素的位置。若該值小於根值，進入該數的左子樹；
• 若該值大於根值，進入該數的右子樹；
• 不滿足條件退出迴圈，表示找到要插入的位置了；
• 如果要插入的值小於標記的值，就把該值放到標記的左子樹裡；
• 如果要插入的值大於標記的值，就把該值放到標記的右子樹裡；

【注】：標記是在查詢迴圈裡用來標記當前節點的上一節點的；因為迴圈條件的原因，退出迴圈時，當前節點肯定為空，而標記就是要插入值的根節點了。

刪除：

• 判斷該樹是否為空，若為空樹，則返回錯誤；
• 查詢將要刪除節點所在位置
• 刪除節點

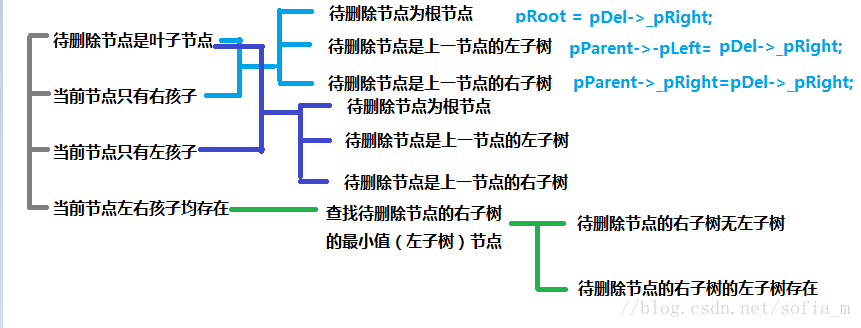
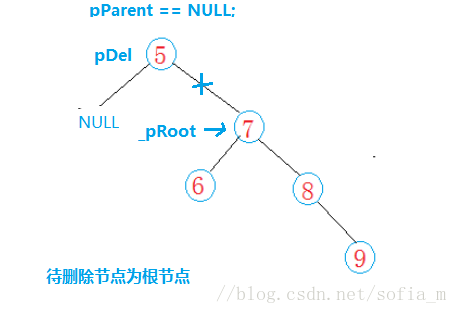
刪除節點則要考慮以下方面：

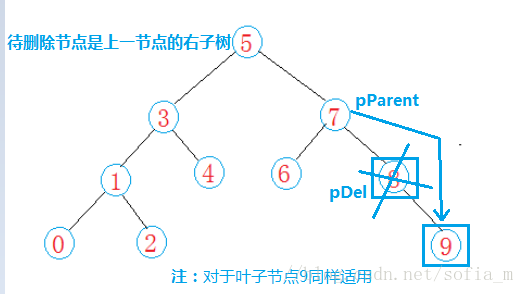
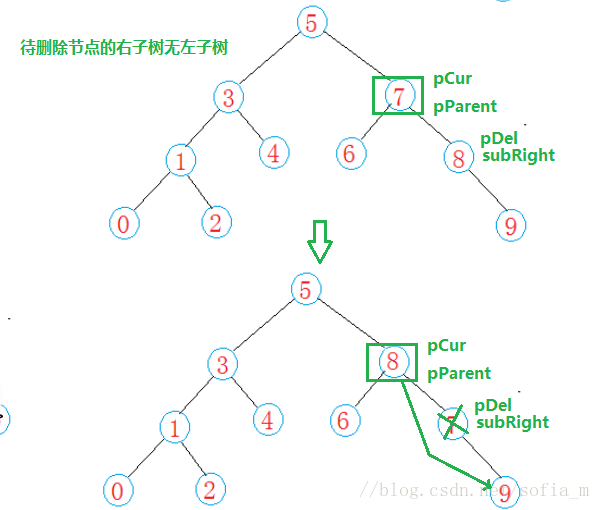
待刪除節點是葉子節點&待刪除節點只有右孩子：

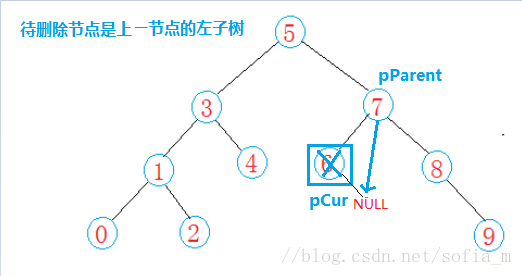
待刪除節點是葉子節點&待刪除節點只有左孩子：

與上一情況（待刪除節點是葉子節點&待刪除節點只有右孩子）差不多，這裡不做過多說明；

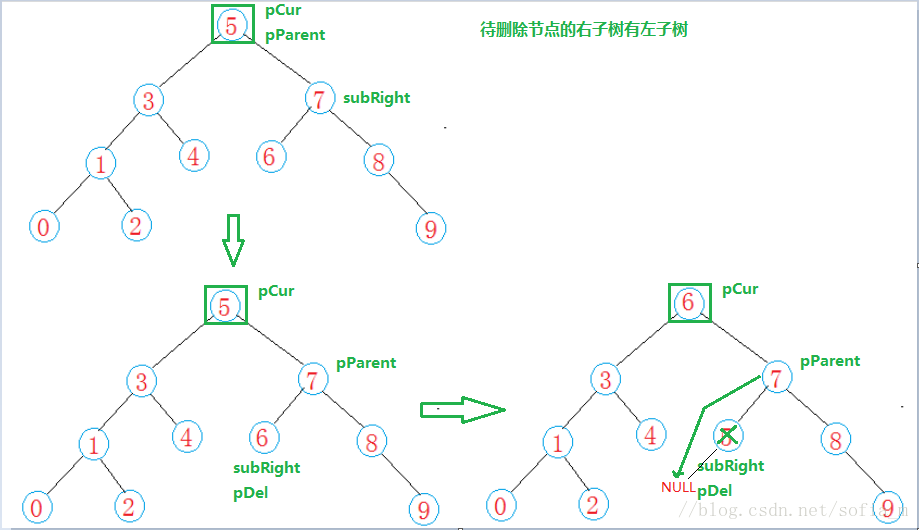
待刪除節點左右孩子均存在：

3、原始碼

【普通版】

BSTree.h

#pragma once
#ifndef __BSTREE_H__
#define __BSTREE_H__
#include<iostream>
#include
 
<assert.h>

using namespace std;

template<class T>
struct BSTreeNode
{
public:
    BSTreeNode(const T& data)
        :_data(data)
        , _pLeft(NULL)
        , _pRight(NULL)
    {}

    BSTreeNode()
        :_pLeft(NULL)
        , _pRight(NULL)
    {}

public:
    BSTreeNode<T>* _pLeft;
    BSTreeNode<T>* _pRight;
    T _data;
};

template<class T>
class BSTree
{
public:
    typedef BSTreeNode<T> Node;
    typedef Node* pNode;

    BSTree()
        :_pRoot(NULL)
    {}

    BSTree(pNode node)
        :_pRoot(node)
    {}

    //查詢
    bool Find(const T& data){
        if (NULL == _pRoot)
            return false;
        pNode pCur = _pRoot;
        while (pCur){
            if (data == pCur->_data)
                return true;
            else if (data > pCur->_data)
                pCur = pCur->_pRight;
            else
                pCur = pCur->_pLeft;
        }
        return false;
    }

    //插入
    bool Insert(const T& data){
        //要插入的為空樹
        if (NULL == _pRoot){
            _pRoot = new Node(data);
            return true;
        }
        //查詢要插入的位置
        pNode pCur = _pRoot;
        pNode pParent = NULL;
        while (pCur){
            if (data == pCur->_data)//樹中已經存在該值
                return false;
            else if (data < pCur->_data){
                pParent = pCur;
                pCur = pCur->_pLeft;
            }
            else{
                pParent = pCur;
                pCur = pCur->_pRight;
            }
        }
        //進行插入操作
        if (data < pParent->_data)
            pParent->_pLeft = new Node(data);
        else
            pParent->_pRight = new Node(data);
        return true;
    }

    //刪除操作
    bool Delete(const T& data){

        //判斷樹是否存在
        if (NULL == _pRoot)
            return false;

        //查詢要刪除的節點
        pNode pCur = _pRoot;
        pNode pParent = NULL;
        pNode pDel = NULL;
        while (pCur){
            if (data > pCur->_data){
                pParent = pCur;
                pCur = pCur->_pRight;
            }
            else if (data < pCur->_data){
                pParent = pCur;
                pCur = pCur->_pLeft;
            }
            else{
                //刪除節點

                //待刪除節點是葉子節點 & 當前節點只有右孩子
                if (NULL == pCur->_pLeft){
                    pDel = pCur;

                    if (NULL == pParent){
                        //待刪除節點是根節點
                        _pRoot = pDel->_pRight;
                    }
                    else if (pDel == pParent->_pLeft){
                        //待刪除節點是上一節點的左子樹
                        pParent->_pLeft = pDel->_pRight;//待刪除節點的左子樹一定為空
                    }
                    else{
                        //待刪除節點是上一節點的右子樹
                        pParent->_pRight = pDel->_pRight;
                    }
                }
                else if (NULL == pCur->_pRight){
                    //待刪除節點是葉子節點 & 當前節點只有左孩子
                    pDel = pCur;
                    if (NULL == pParent){
                        //待刪除節點是根節點
                        _pRoot = pDel->_pLeft;
                    }
                    else if (pDel == pParent->_pLeft){
                        //待刪除節點是上一節點的左子樹
                        pParent->_pLeft = pDel->_pLeft;
                    }
                    else{
                        //待刪除節點是上一節點的右子樹
                        pParent->_pRight = pDel->_pLeft;
                    }
                }
                else{
                    //待刪除節點左右子樹均存在

                    pNode subRight = pCur->_pRight;
                    pParent = pCur;
                    //parent 在這裡不能為空，否則在特定場景下判斷subRight與上一節點的關係時會崩潰

                    //查詢待刪除節點的右子樹的最小值（左子樹）節點
                    while (subRight->_pLeft){
                        pParent = subRight;
                        subRight = subRight->_pLeft;
                    }
                    pDel = subRight;//要刪除的節點

                    //交換待刪除節點和它的右子樹的值，再直接刪除它的右子樹節點
                    pCur->_data = pDel->_data;

                    //還需判斷pDel是pParent的左節點還是右節點
                    //parent 在這裡不能為空的原因，↓
                    if (pDel == pParent->_pLeft)
                        pParent->_pLeft = pDel->_pLeft;
                    else
                        pParent->_pRight = pDel->_pRight;
                }
                delete pDel;
                return true;
            }
        }

        return false;

    }

    //中序遍歷
    void InOrder(){
        _InOrder(_pRoot);
        cout << endl;
    }

    //析構
    ~BSTree(){
        _Destory(_pRoot);
    }

protected:

    void _InOrder(pNode pRoot){
        if (NULL == pRoot)
            return;
        _InOrder(pRoot->_pLeft);
        cout << pRoot->_data << "  ";
        _InOrder(pRoot->_pRight);
    }

    void _Destory(pNode pRoot){
        if (NULL == pRoot)
            return;
        _Destory(pRoot->_pLeft);
        _Destory(pRoot->_pRight);
        delete pRoot;
    }

private:
    pNode _pRoot;
};

#endif //__BSTREE_H__

Test.c

#include"BSTree.h"
#include<Windows.h>
#include<stdio.h>
#include<stdlib.h>
#include<iostream>
using namespace std;

//測試二叉搜尋樹
void test2(){
    int arr[] = { 5, 3, 4, 1, 7, 8, 2, 6, 0, 9 };
    BSTree<int> BSTree;
    //建立二叉搜尋樹
    for (size_t i = 0; i < sizeof(arr) / sizeof(arr[0]); ++i){
        BSTree.Insert(arr[i]);
    }
    BSTree.InOrder();//正確的搜尋二叉樹的中序遍歷一定是有序的
    //檢測查詢6,9,2
    if (BSTree.Find(6))
        cout << "找到了6" << endl;
    else
        cout << "沒找到6" << endl;

    if (BSTree.Find(9))
        cout << "找到了9" << endl;
    else
        cout << "沒找到9" << endl;

    if (BSTree.Find(2))
        cout << "找到了2" << endl;
    else
        cout << "沒找到2" << endl;

    //檢測刪除元素
    BSTree.Delete(4);
    BSTree.InOrder();
    BSTree.Delete(5);
    BSTree.InOrder();
}

int main(){
    test2();
    system("pause");
    return 0;
}

【程式執行結果】