二叉搜尋樹的插入、刪除、查詢等操作:Java語言實現
阿新 • • 發佈:2018-12-24
1 二叉搜尋樹介紹
二叉搜尋樹(BST, Binary Search Tree),也稱二叉排序樹或二叉查詢樹。
二叉搜尋樹:一棵二叉樹,可以為空;如果不為空,滿足以下性質:
1. 非空左子樹的所有鍵值小於其根結點的鍵值。
2. 非空右子樹的所有鍵值大於其根結點的鍵值。
3. 左、右子樹都是二叉搜尋樹。
2 二叉搜尋樹的主要操作
2.1 二叉搜尋樹的查詢操作 查詢從根結點開始,如果樹為空,返回NULL 若搜尋樹非空,則根結點關鍵字和X進行比較, 並進行不同處理:
若X小於根結點鍵值,只需在左子樹中繼續搜尋;
如果X大於根結點的鍵值, 在右子樹中進行繼續搜尋;
若兩者比較結果是相等,搜尋完成,返回指向此結點的指標。
//查詢元素:遞迴方法
BinarySearchTreeNode find(BinarySearchTreeNode root, int data) {
if (root == null)
return null;//查詢失敗
if (data < root.getData())
return find(root.getLeft(),data);//在左子樹中繼續查詢
else if (data > root.getData())
return find(root.getRight(),data);//在右子樹中繼續查詢
else
return root;//查詢成功, 返回找到的結點的地址
}
//查詢元素:非遞迴方法
BinarySearchTreeNode iterFind(BinarySearchTreeNode root, int data) {
while (root != null) {
if (data < root.getData())
root = root.getLeft();//向左子樹中移動, 繼續查詢
else if (data > root.getData())
root = root.getRight();//向右子樹中移動, 繼續查詢
else
return root;//查詢成功, 返回找到的結點的地址
}
return null;//查詢失敗
} 2.2 查詢最大和最小元素
最大元素一定是在樹的最右分枝的端結點上
最小元素一定是在樹的最左分枝的端結點上
//查詢最小元素:遞迴方法 (最小元素一定是在樹的最左分枝的端結點上)
BinarySearchTreeNode findMin(BinarySearchTreeNode root) {
if (root == null)
return null;//空的二叉搜尋樹,返回null
else if (root.getLeft() == null)
return root;//找到最左葉結點並返回
else
return findMin(root.getLeft());//沿左分支繼續查詢
}
//查詢最小元素:非遞迴方法 (最小元素一定是在樹的最左分枝的端結點上)
BinarySearchTreeNode iterFindMin(BinarySearchTreeNode root) {
if (root == null)
return null;//空的二叉搜尋樹,返回null
while (root.getLeft() != null)
root = root.getLeft();//沿左分支繼續查詢
return root;//找到最左葉結點並返回
}
//查詢最大元素:遞迴方法 (最大元素一定是在樹的最右分枝的端結點上)
BinarySearchTreeNode findMax(BinarySearchTreeNode root) {
if (root == null)
return null;//空的二叉搜尋樹,返回null
else if (root.getRight() == null)
return root;//找到最右葉結點並返回
else
return findMax(root.getRight());//沿右分支繼續查詢
}
//查詢最大元素:非遞迴方法 (最大元素一定是在樹的最右分枝的端結點上)
BinarySearchTreeNode iterFindMax(BinarySearchTreeNode root) {
if (root == null)
return null;//空的二叉搜尋樹,返回null
while (root.getRight() != null)
root = root.getRight();//沿右分支繼續查詢
return root;//找到最右葉結點並返回
} 將元素X插入二叉搜尋樹BST中,關鍵是要找到元素應該插入的位置。位置的確定可以利用與查詢函式Find類似的方法,如果在樹BST中找到X,說明要插入的元素已存在,可放棄插入操作。如果沒找到X,查詢終止的位置就是X應插入的位置。
//插入元素
BinarySearchTreeNode insert(BinarySearchTreeNode root, int data) {
if (root == null)
root = new BinarySearchTreeNode(data);//若原樹為空, 生成並返回一個結點的二叉搜尋樹
else {
if (data < root.getData()) //開始找要插入元素的位置
root.setLeft(insert(root.getLeft(),data));//遞迴插入左子樹
else if (data > root.getData())
root.setRight(insert(root.getRight(),data));//遞迴插入右子樹
}
return root;
}2.4 二叉搜尋樹的刪除
考慮三種情況:
要刪除的是葉結點: 直接刪除, 並再修改其父結點指標---置為null
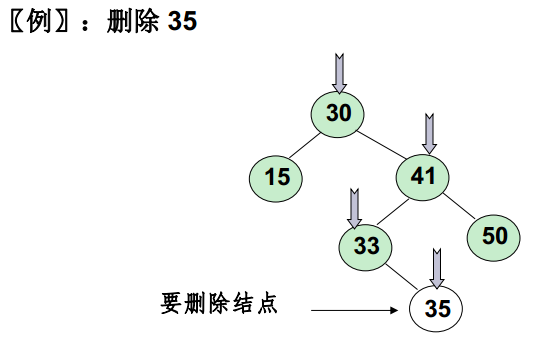
要刪除的結點只有一個孩子結點: 將其父結點的指標指向要刪除結點的孩子結點
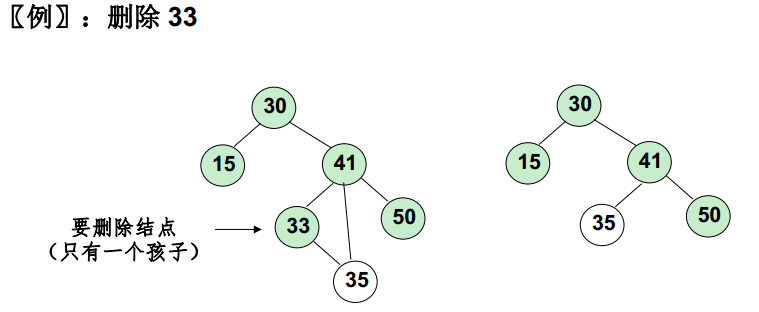
要刪除的結點有左、右兩棵子樹:用另一結點替代被刪除結點: 右子樹的最小元素 或者 左子樹的最大元素
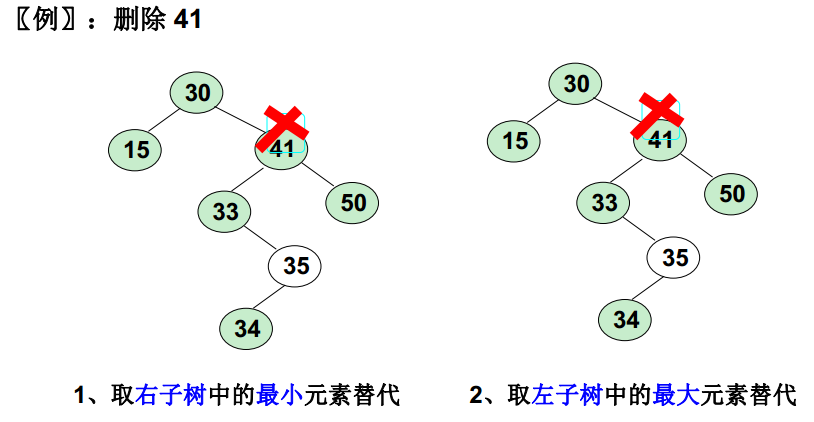
//刪除元素
BinarySearchTreeNode delete(BinarySearchTreeNode root, int data) {
BinarySearchTreeNode temp;
if (root == null)
System.out.println("要刪除的元素未找到");
else if (data < root.getData())
root.setLeft(delete(root.getLeft(),data));//左子樹遞迴刪除
else if (data > root.getData())
root.setRight(delete(root.getRight(),data));//右子樹遞迴刪除
else { //找到要刪除的結點
if (root.getLeft() != null && root.getRight() != null) { //被刪除結點有左右兩個子結點
temp = findMin(root.getRight());//在右子樹中找最小的元素填充刪除結點
root.setData(temp.getData());
root.setRight(delete(root.getRight(),root.getData()));//在刪除結點的右子樹中刪除最小元素
}else { //被刪除結點有一個或無子結點
temp = root;
if (root.getLeft() == null) //有右孩子或無子結點
root = root.getRight();
else if (root.getRight() == null) //有左孩子或無子結點
root = root.getLeft();
temp = null;
}
}
return root;
}2.5 二叉搜尋樹的遍歷
需要注意的是:中序遍歷二叉搜尋樹時,將得到一個有序表。
//中序遍歷:遞迴方法 (中序遍歷二叉搜尋樹時,將得到一個有序表)
void InOrderRecursive(BinarySearchTreeNode root) {
if(root == null)
return;
InOrderRecursive(root.getLeft());//中序遍歷其左子樹
System.out.print(root.getData() + " ");//訪問根結點
InOrderRecursive(root.getRight());//中序遍歷其右子樹
} 3 Java整體程式碼實現
3.1 建立二叉搜尋樹結點類
package Binary_Tree_Study;
/**
* Created by Administrator on 2018/5/20.
*/
public class BinarySearchTreeNode {
private int data;//結點的資料
private BinarySearchTreeNode left;//指向左孩子結點
private BinarySearchTreeNode right;//指向左孩子結點
public BinarySearchTreeNode(int data) {
this.data = data;
this.left = null;
this.right =null;
}
public int getData() {
return data;
}
public void setData(int data) {
this.data = data;
}
public BinarySearchTreeNode getLeft() {
return left;
}
public void setLeft(BinarySearchTreeNode left) {
this.left = left;
}
public BinarySearchTreeNode getRight() {
return right;
}
public void setRight(BinarySearchTreeNode right) {
this.right = right;
}
}
3.2 二叉搜尋樹的上述操作程式碼實現
package Binary_Tree_Study;
/**
* Created by Administrator on 2018/5/20.
*/
public class BinarySearchTree {
private BinarySearchTreeNode root;//根結點
public BinarySearchTree() {
this.root = null;
}
//查詢元素:遞迴方法
BinarySearchTreeNode find(BinarySearchTreeNode root, int data) {
if (root == null)
return null;//查詢失敗
if (data < root.getData())
return find(root.getLeft(),data);//在左子樹中繼續查詢
else if (data > root.getData())
return find(root.getRight(),data);//在右子樹中繼續查詢
else
return root;//查詢成功, 返回找到的結點的地址
}
//查詢元素:非遞迴方法
BinarySearchTreeNode iterFind(BinarySearchTreeNode root, int data) {
while (root != null) {
if (data < root.getData())
root = root.getLeft();//向左子樹中移動, 繼續查詢
else if (data > root.getData())
root = root.getRight();//向右子樹中移動, 繼續查詢
else
return root;//查詢成功, 返回找到的結點的地址
}
return null;//查詢失敗
}
//查詢最小元素:遞迴方法 (最小元素一定是在樹的最左分枝的端結點上)
BinarySearchTreeNode findMin(BinarySearchTreeNode root) {
if (root == null)
return null;//空的二叉搜尋樹,返回null
else if (root.getLeft() == null)
return root;//找到最左葉結點並返回
else
return findMin(root.getLeft());//沿左分支繼續查詢
}
//查詢最小元素:非遞迴方法 (最小元素一定是在樹的最左分枝的端結點上)
BinarySearchTreeNode iterFindMin(BinarySearchTreeNode root) {
if (root == null)
return null;//空的二叉搜尋樹,返回null
while (root.getLeft() != null)
root = root.getLeft();//沿左分支繼續查詢
return root;//找到最左葉結點並返回
}
//查詢最大元素:遞迴方法 (最大元素一定是在樹的最右分枝的端結點上)
BinarySearchTreeNode findMax(BinarySearchTreeNode root) {
if (root == null)
return null;//空的二叉搜尋樹,返回null
else if (root.getRight() == null)
return root;//找到最右葉結點並返回
else
return findMax(root.getRight());//沿右分支繼續查詢
}
//查詢最大元素:非遞迴方法 (最大元素一定是在樹的最右分枝的端結點上)
BinarySearchTreeNode iterFindMax(BinarySearchTreeNode root) {
if (root == null)
return null;//空的二叉搜尋樹,返回null
while (root.getRight() != null)
root = root.getRight();//沿右分支繼續查詢
return root;//找到最右葉結點並返回
}
//插入元素
BinarySearchTreeNode insert(BinarySearchTreeNode root, int data) {
if (root == null)
root = new BinarySearchTreeNode(data);//若原樹為空, 生成並返回一個結點的二叉搜尋樹
else {
if (data < root.getData()) //開始找要插入元素的位置
root.setLeft(insert(root.getLeft(),data));//遞迴插入左子樹
else if (data > root.getData())
root.setRight(insert(root.getRight(),data));//遞迴插入右子樹
}
return root;
}
//刪除元素
BinarySearchTreeNode delete(BinarySearchTreeNode root, int data) {
BinarySearchTreeNode temp;
if (root == null)
System.out.println("要刪除的元素未找到");
else if (data < root.getData())
root.setLeft(delete(root.getLeft(),data));//左子樹遞迴刪除
else if (data > root.getData())
root.setRight(delete(root.getRight(),data));//右子樹遞迴刪除
else { //找到要刪除的結點
if (root.getLeft() != null && root.getRight() != null) { //被刪除結點有左右兩個子結點
temp = findMin(root.getRight());//在右子樹中找最小的元素填充刪除結點
root.setData(temp.getData());
root.setRight(delete(root.getRight(),root.getData()));//在刪除結點的右子樹中刪除最小元素
}else { //被刪除結點有一個或無子結點
temp = root;
if (root.getLeft() == null) //有右孩子或無子結點
root = root.getRight();
else if (root.getRight() == null) //有左孩子或無子結點
root = root.getLeft();
temp = null;
}
}
return root;
}
//中序遍歷:遞迴方法 (中序遍歷二叉搜尋樹時,將得到一個有序表)
void InOrderRecursive(BinarySearchTreeNode root) {
if(root == null)
return;
InOrderRecursive(root.getLeft());//中序遍歷其左子樹
System.out.print(root.getData() + " ");//訪問根結點
InOrderRecursive(root.getRight());//中序遍歷其右子樹
}
//以下函式呼叫相應的方法
public void callFindMin() {
BinarySearchTreeNode cur = findMin(root);
System.out.println("\n最小元素為:" + cur.getData());
}
public void callIterFindMin() {
BinarySearchTreeNode cur = iterFindMin(root);
System.out.println("\n最小元素為:" + cur.getData());
}
public void callFindMax() {
BinarySearchTreeNode cur = findMax(root);
System.out.println("\n最大元素為:" + cur.getData());
}
public void callIterFindMax() {
BinarySearchTreeNode cur = iterFindMax(root);
System.out.println("\n最大元素為:" + cur.getData());
}
public void callInsert(int data) {
root = insert(root, data);
}
public void callDelete(int data) {
root = delete(root, data);
}
public void callInOrderRecursive() {
InOrderRecursive(root);
}
}
3.3 測試
package Binary_Tree_Study;
/**
* Created by Administrator on 2018/5/20.
*/
public class BinarySearchTreeTest {
public static void main(String[] args) {
BinarySearchTree tree = new BinarySearchTree();
/* 建立如下的二叉搜尋樹
5
/ \
3 7
/ \ / \
2 4 6 8 */
tree.callInsert(5);
tree.callInsert(3);
tree.callInsert(2);
tree.callInsert(4);
tree.callInsert(7);
tree.callInsert(6);
tree.callInsert(8);
System.out.println("中序遍歷為:");
tree.callInOrderRecursive();//2 3 4 5 6 7 8
tree.callFindMin();//最小元素為:2
tree.callFindMax();//最大元素為:8
System.out.println("\nD刪除結點資料 2");
tree.callDelete(2);
System.out.println("刪除刪除結點資料2後的中序遍歷為:");
tree.callInOrderRecursive();//3 4 5 6 7 8
tree.callIterFindMin();//最小元素為:3
tree.callIterFindMax();//最大元素為:8
}
}