平衡二叉樹——AVL樹的旋轉操作:Java語言實現
阿新 • • 發佈:2018-12-25
1 前言
2 平衡二叉樹——AVL樹的旋轉操作
2.1 AVL樹的特點
AVL樹本質上還是一棵二叉搜尋樹,它的特點是:
1.本身首先是一棵二叉搜尋樹。
2.帶有平衡條件:每個結點的左右子樹的高度之差的絕對值(平衡因子)最多為1。
也就是說,AVL樹,本質上是帶了平衡功能的二叉查詢樹(二叉排序樹,二叉搜尋樹)。
2.2 AVL樹的定義
package Binary_Tree_Study;
/**
* Created by Administrator on 2018/5/20.
*/
public class AVLTreeNode {
private int data;//結點的資料
private int height;//樹的高度
private AVLTreeNode left;//指向左孩子結點
private AVLTreeNode right;//指向左孩子結點
public AVLTreeNode(int data) {
this.data = data;
this.height = 0;
this.left = null;
this.right =null;
}
public int getData() {
return data;
}
public void setData(int data) {
this.data = data;
}
public int getHeight() {
return height;
}
public void setHeight(int height) {
this.height = height;
}
public AVLTreeNode getLeft() {
return left;
}
public void setLeft(AVLTreeNode left) {
this.left = left;
}
public AVLTreeNode getRight() {
return right;
}
public void setRight(AVLTreeNode right) {
this.right = right;
}
}
2.3 AVL樹的旋轉操作
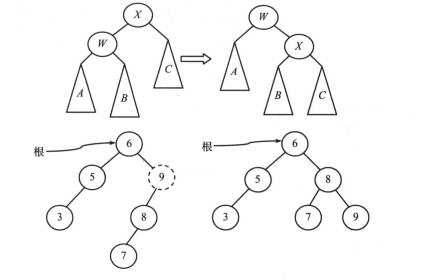
2.3.1 LL旋轉
//LL旋轉
public AVLTreeNode singleRotateLeft(AVLTreeNode x){
AVLTreeNode w= x.getLeft();
x.setLeft(w.getRight());
w.setRight(x);
x.setHeight(Math.max(Height(x.getLeft()),Height(x.getRight()))+1);
w.setHeight(Math.max(Height(w.getLeft()),x.getHeight())+1);
return w;
} //求樹的高度
public int Height(AVLTreeNode root) {
if (root == null)
return -1;
else
return root.getHeight();
}
2.3.2 RR旋轉
//RR旋轉
public AVLTreeNode singleRotateRight(AVLTreeNode w){
AVLTreeNode x= w.getRight();
w.setRight(x.getLeft());
x.setLeft(w);
w.setHeight(Math.max(Height(w.getRight()),Height(w.getLeft()))+1);
x.setHeight(Math.max(Height(x.getRight()),w.getHeight())+1);
return x;
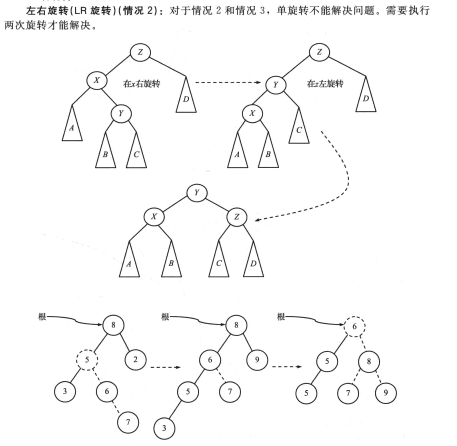
} 2.3.3 LR旋轉
//LR旋轉
public AVLTreeNode doubleRotateLeft(AVLTreeNode z){
z.setLeft(singleRotateRight(z.getLeft()));//在X和Y之間旋轉
return singleRotateLeft(z);//在Z和Y之間旋轉
}2.3.4 RL旋轉
//RL旋轉
public AVLTreeNode doubleRotateRight(AVLTreeNode x){
x.setRight(singleRotateRight(x.getLeft()));//在Z和Y之間旋轉
return singleRotateRight(x);//在X和Y之間旋轉
}3 AVL 樹的插入操作
//插入操作
public AVLTreeNode insert(AVLTreeNode root, int data) {
if (root == null)
root = new AVLTreeNode(data);//若原樹為空, 生成並返回一個結點的AVL樹
else if (data < root.getData()) {
root.setLeft(insert(root.getLeft(),data));
if (Height(root.getLeft())-Height(root.getRight()) == 2)
if (data < root.getLeft().getData())
root = singleRotateLeft(root);
else
root = doubleRotateLeft(root);
} else if (data > root.getData()) {
root.setRight(insert(root.getRight(),data));
if (Height(root.getRight())-Height(root.getLeft()) == 2)
if (data < root.getRight().getData())
root = singleRotateRight(root);
else
root = doubleRotateRight(root);
}
/*否則,資料已經存在,程式什麼也不做。*/
root.setHeight(Math.max(Height(root.getLeft()),Height(root.getRight()))+1);
return root;
}4 參考資料
後記:後續看了一些博文,感覺寫得挺不錯的,在此備註一下,以便以後查閱。