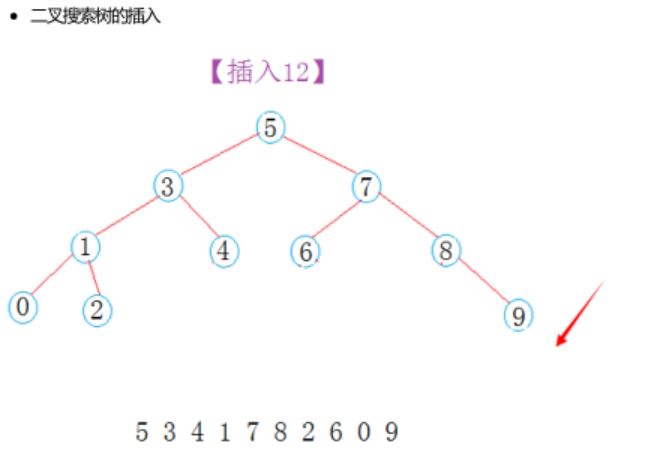
二叉搜尋樹的定義、查詢、插入和刪除
阿新 • • 發佈:2018-12-24
二叉搜尋樹的定義
二叉搜尋樹,也稱有序二叉樹,排序二叉樹,是指一棵空樹或者具有下列性質的二叉樹:
1. 若任意節點的左子樹不空,則左子樹上所有結點的值均小於它的根結點的值;
2. 若任意節點的右子樹不空,則右子樹上所有結點的值均大於它的根結點的值;
3. 任意節點的左、右子樹也分別為二叉查詢樹。
4. 沒有鍵值相等的節點。
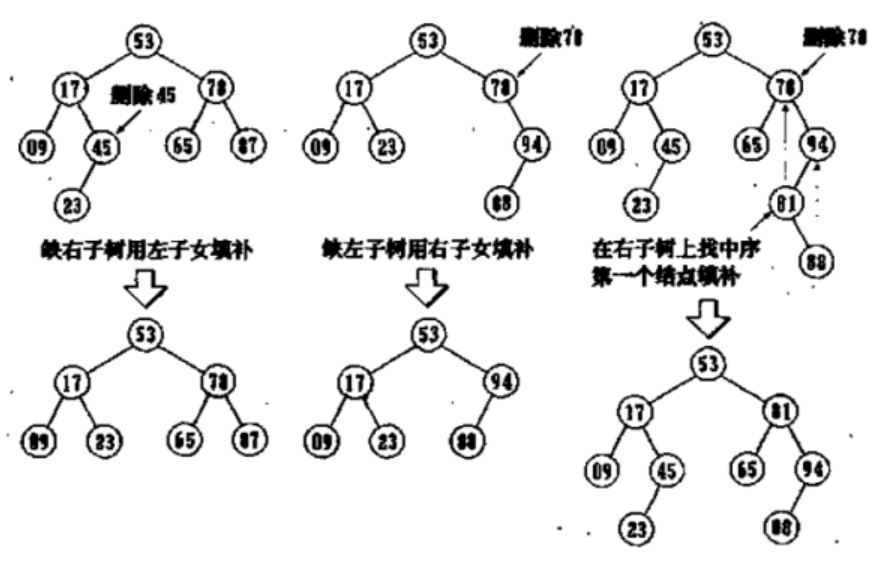
二叉搜尋樹的刪除:
具體實現過程解析:
二叉搜尋樹的結構實現:
//二叉搜尋樹結構 template<class K, class V> struct BSTreeNode { BSTreeNode* _left; BSTreeNode* _right; K _key; V _value; BSTreeNode(const K& key, const V& value) :_left(NULL) ,_right(NULL) ,_key(key) ,_value(value) {} };
查詢實現有迭代和遞迴兩種
迭代法:
//在二叉搜尋樹中查詢節點 Node* Find(const K& key) { Node* cur=_root; //開始遍歷查詢 while (cur) { if (cur->_key > key) { cur = cur->_left; } else if(cur->_key<key) { cur = cur->_right; } else { return cur; } } return NULL; }
遞迴法:
//遞迴查詢法 Node* _Find_R(Node* root, const K& key) { if (root == NULL) { return NULL; } if (root->_key > key) { return _Find_R(root->_left, key); } else if (root->_key < key) { return _Find_R(root->_right, key); } else { return root; } }
刪除迭代法:
//在二叉搜尋樹中刪除節點
bool Remove(const K& key)
{
//沒有節點
if (_root == NULL)
{
return false;
}
//只有一個節點
if (_root->_left == NULL&&_root->_right == NULL)
{
if (_root->_key == key)
{
delete _root;
_root = NULL;
return true;
}
return false;
}
Node* parent = NULL;
Node* cur = _root;
//遍歷查詢要刪除節點的位置
while (cur)
{
Node* del = NULL;
if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else
{
//要刪除節點的左子樹為空,分3種情況
if (cur->_left == NULL)
{
//注意判斷父節點是否為空,若為空,則要刪除的節點為根節點,如:只有根節點5和其右節點9
if (parent == NULL)
{
_root = cur->_right;
delete cur;
cur = NULL;
return true;
}
if (parent->_key > cur->_key)
{
del = cur;
parent->_left = cur->_right;
delete del;
return true;
}
else if (parent->_key < key)
{
del = cur;
parent->_right = cur->_right;
delete del;
return true;
}
}
//要刪除節點的右子樹為空,同樣分3種情況
else if (cur->_right == NULL)
{
//注意判斷父節點是否為空,若為空,則要刪除的節點為根節點,如:只有根節點5和其左節點3
if (parent == NULL)
{
_root = cur->_left;
delete cur;
cur = NULL;
return true;
}
if (parent->_key > cur->_key)
{
del = cur;
parent->_left = cur->_left;
delete del;
return true;
}
else if (parent->_key < cur->_key)
{
del = cur;
parent->_right = cur->_left;
delete del;
return true;
}
}
//左右子樹都不為空
else
{
Node* del = cur;
Node* parent = NULL;
Node* RightFirst = cur->_right;
//右邊第一個節點的左子樹為空
if (RightFirst->_left == NULL)
{
swap(RightFirst->_key, cur->_key);
swap(RightFirst->_value, cur->_value);
del = RightFirst;
cur->_right = RightFirst->_right;
delete del;
return true;
}
//右邊第一個節點的左子樹不為空
while (RightFirst->_left)
{
parent = RightFirst;
RightFirst = RightFirst->_left;
}
swap(RightFirst->_key, cur->_key);
swap(RightFirst->_value, cur->_value);
del = RightFirst;
parent->_left = RightFirst->_right;
delete del;
return true;
}
}
}
return false;
}刪除遞迴法:
bool _Remove_R(Node*& root, const K& key)
{
//沒有節點
if (root == NULL)
{
return false;
}
//只有一個節點
if (root->_left == NULL&&root->_right == NULL)
{
if (root->_key == key)
{
delete root;
root = NULL;
return true;
}
else
{
return false;
}
}
//刪除二叉搜尋樹節點的遞迴寫法
if (root->_key > key)
{
_Remove_R(root->_left, key);
}
else if (root->_key < key)
{
_Remove_R(root->_right, key);
}
else
{
Node* del = NULL;
if (root->_left == NULL)
{
del = root;
root = root->_right;
delete del;
del = NULL;
return true;
}
else if (root->_right == NULL)
{
del = root;
root = root->_left;
delete del;
del = NULL;
return true;
}
else
{
Node* RightFirst = root->_right;
while (RightFirst->_left)
{
RightFirst = RightFirst->_left;
}
swap(root->_key, RightFirst->_key);
swap(root->_value, RightFirst->_value);
_Remove_R(root->_right, key);
return true;
}
}
}插入非遞迴:
//在二叉搜尋樹中插入節點
bool Insert(const K& key, const V& value)
{
if (_root == NULL)
{
_root = new Node(key, value);
}
Node* cur=_root;
Node* parent = NULL;
//首先找到要插入的位置
while (cur)
{
if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else if(cur->_key<key)
{
parent = cur;
cur = cur->_right;
}
else
{
return false;
}
}
//在找到插入位置以後,判斷插入父親節點的左邊還是右邊
if (parent->_key > key)
{
parent->_left = new Node(key, value);
}
else
{
parent->_right = new Node(key, value);
}
return true;
}
插入遞迴:
//遞迴插入法
bool _Insert_R(Node*& root, const K& key, const V& value)
{
if (root == NULL)
{
root = new Node(key, value);
return true;
}
if (root->_key > key)
{
return _Insert_R(root->_left, key, value);
}
else if(root->_key < key)
{
return _Insert_R(root->_right, key, value);
}
else
{
return false;
}
}當二叉搜尋樹出現如下圖情形時,效率最低:
完整程式碼及測試實現如下:
#include<iostream>
using namespace std;
//二叉搜尋樹結構
template<class K, class V>
struct BSTreeNode
{
BSTreeNode* _left;
BSTreeNode* _right;
K _key;
V _value;
BSTreeNode(const K& key, const V& value)
:_left(NULL)
,_right(NULL)
,_key(key)
,_value(value)
{}
};
template<class K,class V>
class BSTree
{
typedef BSTreeNode<K, V> Node;
public:
BSTree()
:_root(NULL)
{}
//在二叉搜尋樹中插入節點
bool Insert(const K& key, const V& value)
{
if (_root == NULL)
{
_root = new Node(key, value);
}
Node* cur=_root;
Node* parent = NULL;
//首先找到要插入的位置
while (cur)
{
if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else if(cur->_key<key)
{
parent = cur;
cur = cur->_right;
}
else
{
return false;
}
}
//在找到插入位置以後,判斷插入父親節點的左邊還是右邊
if (parent->_key > key)
{
parent->_left = new Node(key, value);
}
else
{
parent->_right = new Node(key, value);
}
return true;
}
//在二叉搜尋樹中查詢節點
Node* Find(const K& key)
{
Node* cur=_root;
//開始遍歷查詢
while (cur)
{
if (cur->_key > key)
{
cur = cur->_left;
}
else if(cur->_key<key)
{
cur = cur->_right;
}
else
{
return cur;
}
}
return NULL;
}
//在二叉搜尋樹中刪除節點
bool Remove(const K& key)
{
//沒有節點
if (_root == NULL)
{
return false;
}
//只有一個節點
if (_root->_left == NULL&&_root->_right == NULL)
{
if (_root->_key == key)
{
delete _root;
_root = NULL;
return true;
}
return false;
}
Node* parent = NULL;
Node* cur = _root;
//遍歷查詢要刪除節點的位置
while (cur)
{
Node* del = NULL;
if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else
{
//要刪除節點的左子樹為空,分3種情況
if (cur->_left == NULL)
{
//注意判斷父節點是否為空,若為空,則要刪除的節點為根節點,如:只有根節點5和其右節點9
if (parent == NULL)
{
_root = cur->_right;
delete cur;
cur = NULL;
return true;
}
if (parent->_key > cur->_key)
{
del = cur;
parent->_left = cur->_right;
delete del;
return true;
}
else if (parent->_key < key)
{
del = cur;
parent->_right = cur->_right;
delete del;
return true;
}
}
//要刪除節點的右子樹為空,同樣分3種情況
else if (cur->_right == NULL)
{
//注意判斷父節點是否為空,若為空,則要刪除的節點為根節點,如:只有根節點5和其左節點3
if (parent == NULL)
{
_root = cur->_left;
delete cur;
cur = NULL;
return true;
}
if (parent->_key > cur->_key)
{
del = cur;
parent->_left = cur->_left;
delete del;
return true;
}
else if (parent->_key < cur->_key)
{
del = cur;
parent->_right = cur->_left;
delete del;
return true;
}
}
//左右子樹都不為空
else
{
Node* del = cur;
Node* parent = NULL;
Node* RightFirst = cur->_right;
//右邊第一個節點的左子樹為空
if (RightFirst->_left == NULL)
{
swap(RightFirst->_key, cur->_key);
swap(RightFirst->_value, cur->_value);
del = RightFirst;
cur->_right = RightFirst->_right;
delete del;
return true;
}
//右邊第一個節點的左子樹不為空
while (RightFirst->_left)
{
parent = RightFirst;
RightFirst = RightFirst->_left;
}
swap(RightFirst->_key, cur->_key);
swap(RightFirst->_value, cur->_value);
del = RightFirst;
parent->_left = RightFirst->_right;
delete del;
return true;
}
}
}
return false;
}
bool Insert_R(const K& key, const V& value)
{
return _Insert_R(_root, key, value);
}
Node* Find_R(const K& key)
{
return _Find_R(_root, key);
}
bool Remove_R(const K& key)
{
return _Remove_R(_root, key);
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
protected:
bool _Remove_R(Node*& root, const K& key)
{
//沒有節點
if (root == NULL)
{
return false;
}
//只有一個節點
if (root->_left == NULL&&root->_right == NULL)
{
if (root->_key == key)
{
delete root;
root = NULL;
return true;
}
else
{
return false;
}
}
//刪除二叉搜尋樹節點的遞迴寫法
if (root->_key > key)
{
_Remove_R(root->_left, key);
}
else if (root->_key < key)
{
_Remove_R(root->_right, key);
}
else
{
Node* del = NULL;
if (root->_left == NULL)
{
del = root;
root = root->_right;
delete del;
del = NULL;
return true;
}
else if (root->_right == NULL)
{
del = root;
root = root->_left;
delete del;
del = NULL;
return true;
}
else
{
Node* RightFirst = root->_right;
while (RightFirst->_left)
{
RightFirst = RightFirst->_left;
}
swap(root->_key, RightFirst->_key);
swap(root->_value, RightFirst->_value);
_Remove_R(root->_right, key);
return true;
}
}
}
//遞迴查詢法
Node* _Find_R(Node* root, const K& key)
{
if (root == NULL)
{
return NULL;
}
if (root->_key > key)
{
return _Find_R(root->_left, key);
}
else if (root->_key < key)
{
return _Find_R(root->_right, key);
}
else
{
return root;
}
}
//遞迴插入法
bool _Insert_R(Node*& root, const K& key, const V& value)
{
if (root == NULL)
{
root = new Node(key, value);
return true;
}
if (root->_key > key)
{
return _Insert_R(root->_left, key, value);
}
else if(root->_key < key)
{
return _Insert_R(root->_right, key, value);
}
else
{
return false;
}
}
void _InOrder(Node* root)
{
if (root == NULL)
{
return;
}
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}
protected:
Node* _root;
};
void Test()
{
BSTree<int, int> s;
//測試插入
s.Insert_R(5, 1);
s.Insert_R(4, 1);
s.Insert_R(3, 1);
s.Insert_R(6, 1);
s.Insert_R(1, 1);
s.Insert_R(2, 1);
s.Insert_R(0, 1);
s.Insert_R(9, 1);
s.Insert_R(8, 1);
s.Insert_R(7, 1);
//二叉搜尋樹按中序輸出是有序的
s.InOrder();
//測試查詢
cout << s.Find_R(6)->_key << endl;
//測試刪除
s.Remove(4);
s.Remove(6);
s.Remove(3);
s.Remove(1);
s.Remove(2);
//再次列印刪除後的結果
s.InOrder();
}
int main()
{
Test();
system("pause");
return 0;
}
執行結果:
0 1 2 3 4 5 6 7 8 9
6
0 5 7 8 9
請按任意鍵繼續. . .