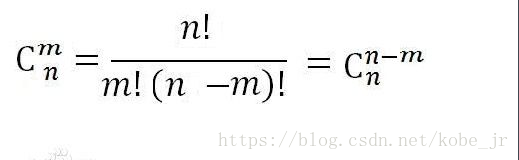組合數：C(n, m) ;         組合數取模：C(n, m) % mod，mod是一個很大的數。

1.公式：

2.性質：（1）C(n,m)= C(n,n-m)   其中有C(n, 0) = 1;

（2）C(n,m)=C(n-1,m-1)+C(n-1,m)。可以用作遞迴中的公式。

性質2和楊輝三角的相似性（核心部分就是利用了性質2）。

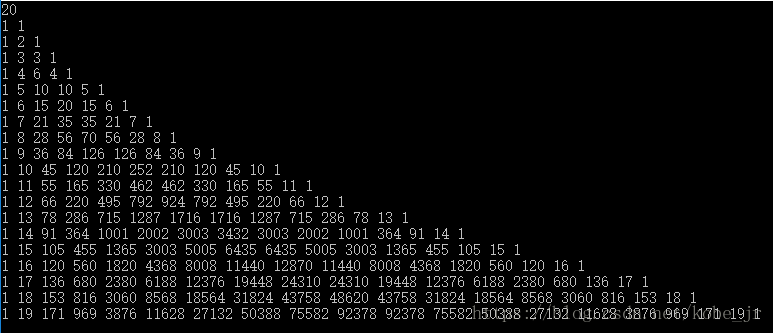
例題：列印楊輝三角：

#include<iostream>
using namespace std;
int a[100][100];
int main(){
    int n;
    while(cin >> n){
       a[0][0] = 1; a[0][1] = 1;
       for(int i = 1; i < n - 1; i ++){
       		for(int j = 0; j < i + 2; j ++){
       			a[i][j] = a[i - 1][j - 1] + a[i - 1][j];
			} 
           
       }
        
       for(int i = 0; i < n - 1; i ++){
           for(int j = 0; j < i + 1; j ++){
               cout << a[i][j] << " ";
           }
           cout << a[i][i + 1] << endl;
    	}
      
	}
 	return 0;
}
 

列印前20的矩陣：

當數很大時，顯然複雜度太大，所以這裡使用拓展歐幾里得和費馬小定理的方法求解。

1、拓展歐幾里德：(gcd就是求最大公約數)

給定模數m，求a的逆相當於求解ax=1(mod m)
這個方程可以轉化為ax-my=1 
然後套用求二元一次方程的方法，用擴充套件歐幾里得演算法求得一組x0,y0和gcd 
檢查gcd是否為1 
gcd不為1則說明逆元不存在 

若為1，則調整x0到0~m-1的範圍中即可。

//拓展歐幾里得演算法求逆元 
void exgcd(ll a, ll b, ll &x, ll &y) {  
    if(!b){
		x = 1; 
		y = 0;
	} 
	else{
		exgcd(b, a % b, y, x);  
    	y -= (a / b) * x;
	}    
}  
  
ll inv(ll a, ll n) {  
    ll x, y;  
    exgcd(a, n, x, y);  
    return (x + n) % n;  
} 
 

2、費馬小定理：

在模為素數p的情況下，有費馬小定理 
a^(p-1)=1（mod p） 
那麼a^(p-2)=a^-1(mod p) 

也就是說a的逆元為a^(p-2)。

費馬小定理求逆元
ll pow(ll a, ll n, ll p)    //快速冪 a^n % p
{
    ll ans = 1;
    while(n)
    {
        if(n & 1) ans = ans * a % p;
        a = a * a % p;
        n >>= 1;
    }
    return ans;
}

ll inv(ll a, ll b)   //費馬小定理求逆元
{
    return pow(a, b - 2, b);
}	
 

這裡的兩個定理在很多oj上的求解組合數取模之類的問題應用是否廣泛，此外這裡還用到了求解最大公約數（歐幾里得輾轉相除法)以及快速冪的方法，這類的基本演算法應當十分熟悉。

以上。歡迎您提出寶貴的意見，讓我們一同進步。謝謝！