在微信公眾號中看到一個很有趣的題目：

假如你是一名人事經理，你要招聘一名資料分析師，目前有100名面試者，你該如何抉擇？

應聘流程：

這100人隨機排序，逐一面試，每當一位候選人面試完後，要麼錄用，要麼不選。如果選擇了他，不再考慮後面的人。你必須從中選擇一人，如果前99都看不中，必須選擇最後一人。那麼你怎麼保證自己最高概率錄取到能力最強的人

尤拉數：e

e^{i\pi}+1=0，含義是單位時間內，持續翻倍增長所能達到的極限值。如何理解？
比如：一個細胞單位時間24h可以分裂一次，那麼24h後：
(1+1)^1=2
如果12h分裂一次，那麼24h後：
(1+1/2)^2=2.25
如果24/n h內分裂一次，那麼24h後：
(1+1/n)^n \to e

我們的問題答案就是100／e＝37 ，pass掉前37人，從第38人開始選擇大於前37人能力的第一個人作為錄取者。

37％法則，我們通過實驗來證明一下：我們選擇100個應聘者，編號1－100。隨機打亂順序，按照37％法則選取，程式執行1w次後，我們看看結果。

#100個人招聘能力最好的人，怎麼保證最大概率找到最合適的人才，只選一人，一旦選擇不考慮其他，如一直不選擇，選最後一位。

import random
#mport numpy as np
#import itertools
#import math
import matplotlib.pyplot as plt
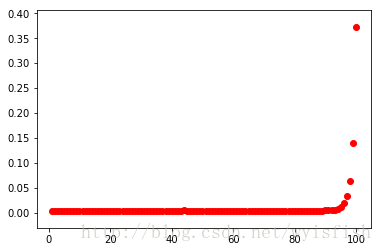
from collections import
 
 defaultdict

number = 100
n=100000
def generate(n):
    dict=defaultdict()
    L=[j for j in range(1,number+1)]
    for i in range(n):
        random.shuffle(L)
        mid=int(number*0.37)
        L_left=L[:mid]
        L_right=L[mid:]
        best_out=max(L_left)
        choose = choose1(best_out,L_right)
        if
 
 choose in dict:
            dict[choose]=dict[choose]+1
        else:
            dict[choose]=1
    return dict

def choose1(best_out,List_right):
    m=len(List_right)
    for i in range(m):
        if List_right[i]>best_out:
            choose=List_right[i]
            return choose
    choose=List_right[-1]
    return choose

dict=generate(n)
dict
x=[int(i) for i,_ in dict.items() ]
y=[float(i/n) for _,i in dict.items() ]
#print(x)
#print(y)

plt.scatter(x,y,color='r')

plt.show()

圖中X座標表示最後錄取者的能力值，Y表示在1w次中所佔比重，我們可以看到有接近40%的時候會選到最好的候選人，說明37％準則是比較準確的。