2.詞法分析

詞法分析的目的是什麼呢？ 是把一長串的字元分解成一個個的詞素，並且生成（id，2）這種作為語法分析的基礎。

首先是詞法單元，詞素等的定義。

然後是如何輸入。

三是輸入後如何識別。

識別後如何組成中間式子。

  1.三個關鍵詞

詞法單元，詞素，模式

1. 詞法單元： 詞法單元由一個詞法單元名和一個可選的屬性值組成。

詞法單元名是一個表示某種詞法單位的抽象符號。比如一個特定的關鍵字

或者代表一個識別符號的輸入字元序列。詞法單元名字是語法分析器的輸入符號。

2．模式 描述了一個詞法單元的詞素可能具有的形式。 比如if 關鍵字，模式是對

語法或者詞法中你某些特定的字元的抽象表達。 比如  識別符號，關鍵字，等

3.詞素，源程式的一個字元序列。

 

2.輸入緩衝 ---進行詞法分析最首先的是要進行字串的輸入。

如何輸入也是一個問題。

1. 如果一個字元一個字元的輸入，則顯得太快緩慢。而全部讀入這太佔記憶體。所以這裡有了一個輸入緩衝的概念。

2.就是進行詞法分析的時候，只讀一個字元是無法分析這個詞素屬於什麼模式。是一個識別符號還是關鍵字，還是界符之類的。所以就有了超前搜尋這個概念。

至少必須向前多查詢一個字元做比對才知道這個詞素屬於什麼模式

3.為什麼需要緩衝區對？

緩衝區是為了加快讀入資料的效率，當輸入字元超長的時候，一個緩衝區並不能完全識別串，所以需要緩衝區對。然後又加入了哨兵標記。

那麼哨兵標記是幹什麼的呢？

 

 

3.詞法規約：

       3.1.串和語言 這裡的定義的串和語言比較泛化。不夠深入和詳盡。也可以表示為集合。

暫且理解為串是字母表符號的有限集合，而語言是串的集合

串： {a,b,v,d,s,s,}  

語言：{{a,v,c,,s},{dwmme,r,r,t,q,r}}

 

上圖中確實很好的解釋了串和語言了

L {A,B,…,a,b,…z}   

D {0,1,2,3,4,5,…,9} 

將L看成是大小寫字母組成的字母表，將D看成是10個數位組成的字母表。

另一種方法是將L和D看做語言，他們的所有串的長度都為1.  A是長度為1的串 ，1,也是長度為1的串。

 

 

         1.串是一個字母表符號的有限集合。而字元表是一個有限的符號集合。符號包括了數字，字母和標點符號。{a,b,c,d,e}

         2.語言：語言是給定某個字母表上一個任意的可數的串的集合。

            {a,ab,abc,ed,treeeasdasa}

 3.閉包

編譯原理的閉包：

 V是一個符號集合，假設V指的是三個符號a, b, c的集合，記為 V = {a, b, c }
V* 讀作“V的閉包”，它的數學定義是V自身的任意多次自身連線（乘法）運算的積，也是一個集合。
也就是說，用V中的任意符號進行任意多次（包括0次）連線，得到的符號串，都是V*這個集合中的元素。
0次連線的結果是不含任何符號的空串，記為 ε
1次連線就是隻有一個符號的符號串，比如，a，b， c
2次連線是兩個符號構成的符號串，比如，aa, ab, ac, ba, bb, bc,等等

3.2  閉包的解釋

 

 

3.2.1 編譯原理書籍閉包解釋：閉包和正則

正則表示式的最基本概念來重新介紹一次，主要想讓大家更深地理解它。首先我們要重新定義一下“語言”這個概念。“語言”就是指字串的集合，其中的字元來自於一個有限的字元集合。也就是說，語言總要定義在一個有限的字符集上，但是語言本身可以既可以是有窮集合，也可以是無窮集合。比如“C#語言”就是指滿足C#語法的全體字串的集合，它顯然是個無窮集合。當然也可以定義一些簡單的語言，比如這個語言{ a }就只有一個成員，那就是一個字母a。後面我們都用大括號{}來表示字串的集合。所謂正則表示式呢，就是描述一類語言的一種特殊表示式，正則表示式共有2種基本要素：

1. 表示式ε表示一個語言，僅包含一個長度為零的字串，可以理解為{ String.Empty }，我們通常把String.Empty記作ε，讀作epsilon。
2. 對字符集中任意字元a，表示式a表示僅有一個字元a的語言，即{ a }。

同時正則表示式定義了3種基本運算規則：

1. 兩個正則表示式的並，記作X|Y，表示的語言是正則表示式X所表示的語言與正則表示式Y所表示語言的並集。比如a|b所得的語言就是{a, b}。類似於加法
2. 兩個正則表示式的連線，記作XY，表示的語言是將X的語言中每個字串後面連線上Y語言中的每一種字串，再把所有這種連線的結果組成一種新的語言。比如令X = a|b，Y = c|d，那麼XY所表示的語言就是{ac, bc, ad, bd}。因為X表示是{a, b}，而Y表示的是{ c, d}，連線運算取X語言的每一個字串接上Y語言的每一個字串，最後得到了4種連線結果。這類似於乘法
3. 一個正則表示式的克林閉包，記作X*，表示分別將零個，一個，兩個……無窮個X與自己連線，然後再把所有這些求並。也就是說X* = ε | X | XX | XXX | XXX | ……。比如a*這個正則表示式，就表示的是個無窮語言{ ε, a, aa, aaa, aaaa, …. }。這相當於任意次重複一個語言。

以上三種運算寫在一起時克林閉包的優先順序高於連線運算，而連線運算的優先順序高於並運算。以上就是正則表示式的全部規則！並不是很難理解對吧？下面我們用正則表示式來描述一下剛才各個詞素的規則。

 

首先是關鍵字string，剛才我們描述說它是“正好是s-t-r-i-n-g這幾個字母按順序組成”，用正則表示式來表示，那就是s-t-r-i-n-g這幾個字母的連線運算，所以寫成正則表達是就是string。大家一定會覺得這個例子很無聊。。那麼我們來看下一個例子：識別符號。用白話來描述是“由字母開頭，後面可以跟零個或多個字母或數字”。先用正則表示式描述“由字母開頭”，那就是指，可以是a-z中任意一個字母來開頭。這是正則表示式中的並運算：a|b|c|d|e|f|g|h|i|j|k|l|m|n|o|p|q|r|s|t|u|v|w|x|y|z。如果每個正則表示式都這麼寫，那真是要瘋掉了，所以我們引入方括號語法，寫在方括號裡就表示這些字元的並運算。比如[abc]就表示a|b|c。而a-z一共26個字母我們也簡寫成a-z，這樣，“由字母開頭”就可以翻譯成正則表示式[a-z]了。接下來我們翻譯第二句“後面可以跟零個或多個字母或數字”這句話中的“零個或多個”可以翻譯成克林閉包運算，最後相信大家都可以寫出來，就是[a-z0-9]*。最後，前後兩句之間是一個連線運算，因此最後描述識別符號“語言”的正則表示式就是[a-z][a-z0-9]*。其中的*運算也意味著“識別符號”是一種無窮語言，有無數種可能的識別符號。本來就是這樣，很好理解對吧？

 

從上面例子可以看出，正則表示式都可以用兩種要素和三種基本運算組合出來。但是如果我們要真的拿來描述詞法單詞的規則，需要一些便於使用的輔助語法，就像上邊的方括號語法那樣。我們定義一些正則表示式的擴充套件運算：

1. 方括號表示括號內的字元並運算。[abc]就等於a|b|c
2. 方括號中以^字元開頭，表示字符集中，排除方括號中的所有字元之後，所剩字元的並運算。[^ab]就表示除了ab以外所有字元求並。
3. 圓.點表示字符集內所有字元的並。因此 .* 這個表示式就能表示這種字符集所能組成的一切字串。
4. X?表示 X|ε 。表示X與空字串之間可選。
5. X+表示XX*。這等於限制了X至少要重複1次。

用過正則表示式的同學應該都熟悉以上運算了。其實.NET中的正則表示式還提供更多的擴充套件語法，但我們這次並不使用.NET的正則庫，所以就不列出其餘的語法了。

 

我們把所有能用正則表示式表示的語言稱作正則語言。很遺憾，並非所有的語言都是正則語言。比如C#，或者所有程式語言、HTML、XML、JSON等等，都不是正則語言。所以不能用正則表示式定義上述語言的規則。但是，用正則表示式來定義詞法分析的規則卻是非常合適的。大部分程式語言的詞素都可以用一個簡單的正則表示式來表達。下面就是上述單詞的正則表示式定義。

 

為什麼需要閉包。因為編譯原理是在一個字元長串或者集合中找到正確的詞。

 

閉包之後是正則表示式

（letter_|digit）*就是閉包運算。通過閉包運算來形成表示式。

我們數學中也有運算，比如 a+b  1+2 然後  1+2=3 這就形成了表示式 1+2是一個加法表示式。  + 表示加法運算。  閉包表示閉包運算。通過運算形成表示式。通過表示式形成自動機，其實自動機可以算成是等式。

什麼是式，是一種格式，規範等。 表示式，算式，等式。

什麼是正則表示式。 表示正則關係的規範。

 

3.2.2二元關係理解閉包：

 

集合X與集合Y上的二元關係是R=(X,Y,G(R))，其中G(R)，稱為R的圖，是笛卡兒積X×Y的子集。若 (x,y) ∈G(R) ，則稱x是R-關係於y，並記作xRy或R(x,y)。否則稱x與y無關係R。但經常地我們把關係與其圖等同起來，即：若R⊆X×Y，則R是一個關係。

例如：有四件物件 {球，糖，車，槍} 及四個人 {甲，乙，丙，丁}。 若甲擁有球，乙擁有糖，及丁擁有車，即無人有槍及丙一無所有— 則二元關係"為...擁有"便是R=({球，糖，車，槍}, {甲，乙，丙，丁}, {(球,甲), (糖,乙), (車,丁)})。

其中 R 的首項是物件的集合，次項是人的集合，而末項是由有序對（物件，主人）組成的集合。比如有序對（球，甲）∈G(R)，所以我們可寫作"球R甲"，表示球為甲所擁有。

不同的關係可以有相同的圖。以下的關係 ({球，糖，車，槍}, {甲，乙，丁}, {(球,甲), (糖,乙), (車,丁)} 中人人皆是物主，所以與R不同，但兩者有相同的圖。話雖如此，我們很多時候索性把R定義為G(R)， 而 "有序對 (x,y) ∈G(R)" 亦即是 "(x,y) ∈R"。

二元關係可看作成二元函式，這種二元函式把輸入元x∈X及y∈Y視為獨立變數並求真偽值（即“有序對(x,y) 是或非二元關係中的一元”此一問題）。

若X=Y，則稱R為X上的關係。

進行關係運算。

 

3.2.3數學中的閉包：

數學中是閉的集合,也就是集合和它的邊界的並。集合e的全體聚點並上e稱為e的閉包。關係的閉包運算時關係上的一元運算，它把給出的關係R擴充成一新關係R’，使R’具有一定的性質，且所進行的擴充又是最“節約”的。
比如自反閉包，相當於把關係R對角線上的元素全改成1，其他元素不變，這樣得到的R’是自反的，且是改動次數最少的，即是最“節約”的。

什麼是聚點？

在拓撲學、數學分析和複分析中都有聚點的概念。
在拓撲學中設拓撲空間(X，τ)，A⊆X，x∈X。若x的每個鄰域都含有A \ {x}中的點，則稱x為A的聚 點。
在數學分析中座標平面上具有某種性質的點的集合，稱為平面點集。給定點集E ，對於任意給定的δ〉0 ，點P 的δ去心鄰域內，總有E 中點，則稱為P 是 E的聚點（或叫作極限點）。
聚點可以是E中的點，也可以不屬於E。此聚點要麼是內點，要麼是邊界點。內點是聚點，界點是聚點，孤立點不是聚點。對於有限點集是不存在聚點的。聚點必須相對給定的集合而言，離開了點集E，聚點就沒有意義。
在複分析中點集E，若在複平面上的一點z的任意鄰域都有E的無窮多個點，則稱z為E的聚點。
以聚點為圓心，任意大的半徑大ε>0畫一圓，總有無窮多個點匯聚在該圓內。若聚點是唯一的，則聚點就是極限點。

 

3.2.4 Js中的閉包。更像java的內部類的概念。那麼為什麼要取名閉包？？

 

閉包就是能夠讀取其他函式內部變數的函式。例如在javascript中，只有函式內部的子函式才能讀取區域性變數，所以閉包可以理解成“定義在一個函式內部的函式“。在本質上，閉包是將函式內部和函式外部連線起來的橋樑。

 

本質

集合 S 是閉集當且僅當 Cl(S)=S（這裡的cl即closure，閉包）。特別的，空集的閉包是空集，X 的閉包是 X。集合的交集的閉包總是集合的閉包的交集的子集（不一定是真子集）。有限多個集合的並集的閉包和這些集合的閉包的並集相等；零個集合的並集為空集，所以這個命題包含了前面的空集的閉包的特殊情況。無限多個集合的並集的閉包不一定等於這些集合的閉包的並集，但前者一定是後者的父集。

若 A 為包含 S 的 X 的子空間，則 S 在 A 中計算得到的閉包等於 A 和 S 在 X 中計算得到的閉包（Cl_A(S) = A ∩ Cl_X(S））的交集。特別的，S在 A 中是稠密的，當且僅當 A 是 Cl_X(S) 的子集。

 

如果一個程式語言容許函式遞迴另一個函式的話 （像 Perl 就是），閉包便具有意義。要注意的是，有些語言雖提供匿名函式的功能，但卻無法正確處理閉包； Python 這個語言便是一例。如果要想多瞭解閉包的話，建議你去找本功能性程式 設計的教科書來看。Scheme這個語言不僅支援閉包，更鼓勵多加使用。

 

閉包是函式和宣告該函式的詞法環境的組合。

 

詞法作用域

考慮如下情況：

 

function init() {

var name = "Mozilla"; // name 是一個被 init 建立的區域性變數

n displayName() { // displayName() 是內部函式,一個閉包

alert(name); // 使用了父函式中 宣告的變數

}

displayName();

}

init();

init() 建立了一個區域性變數 name 和一個名為 displayName() 的函式。displayName() 是定義在 init() 裡的內部函式，僅在該函式體內可用。displayName() 內沒有自己的區域性變數，然而它可以訪問到外部函式的變數，所以 displayName() 可以使用父函式 init() 中宣告的變數 name 。但是，如果有同名變數 name 在 displayName() 中被定義，則會使用的 displayName() 中定義的 name 。

 

執行程式碼可以發現 displayName() 內的 alert() 語句成功的顯示了在其父函式中宣告的 name 變數的值。這個詞法作用域的例子介紹了引擎是如何解析函式巢狀中的變數的。詞法作用域中使用的域，是變數在程式碼中宣告的位置所決定的。巢狀的函式可以訪問在其外部宣告的變數。

 

閉包

現在來考慮如下例子 ：

 

function makeFunc() {

var name = "Mozilla";

function displayName() {

alert(name);

}

return displayName;

}

 

var myFunc = makeFunc();

myFunc();

執行這段程式碼和之前的 init() 示例的效果完全一樣。其中的不同 — 也是有意思的地方 — 在於內部函式 displayName() 在執行前，被外部函式返回。

 

第一眼看上去，也許不能直觀的看出這段程式碼能夠正常執行。在一些程式語言中，函式中的區域性變數僅在函式的執行期間可用。一旦 makeFunc() 執行完畢，我們會認為 name 變數將不能被訪問。然而，因為程式碼執行的沒問題，所以很顯然在 JavaScript 中並不是這樣的。

 

這個謎題的答案是，JavaScript中的函式會形成閉包。 閉包是由函式以及建立該函式的詞法環境組合而成。這個環境包含了這個閉包建立時所能訪問的所有區域性變數。在我們的例子中，myFunc 是執行 makeFunc 時建立的 displayName 函式例項的引用，而 displayName 例項仍可訪問其詞法作用域中的變數，即可以訪問到 name 。由此，當 myFunc 被呼叫時，name 仍可被訪問，其值 Mozilla 就被傳遞到alert中。

 

下面是一個更有意思的示例 — makeAdder 函式：

 

function makeAdder(x) {

return function(y) {

return x + y;

};

}

 

var add5 = makeAdder(5);

var add10 = makeAdder(10);

 

console.log(add5(2));  // 7

console.log(add10(2)); // 12

在這個示例中，我們定義了 makeAdder(x) 函式，他接受一個引數 x ，並返回一個新的函式。返回的函式接受一個引數 y，並返回x+y的值。

 

從本質上講，makeAdder 是一個函式工廠 — 他建立了將指定的值和它的引數相加求和的函式。在上面的示例中，我們使用函式工廠建立了兩個新函式 — 一個將其引數和 5 求和，另一個和 10 求和。

 

add5 和 add10 都是閉包。它們共享相同的函式定義，但是儲存了不同的詞法環境。在 add5的環境中，x 為 5。而在 add10 中，x 則為 10。

 

實用的閉包

閉包很有用，因為他允許將函式與其所操作的某些資料（環境）關聯起來。這顯然類似於面向物件程式設計。在面向物件程式設計中，物件允許我們將某些資料（物件的屬性）與一個或者多個方法相關聯。

 

 

 

 

 

因此，通常你使用只有一個方法的物件的地方，都可以使用閉包。

 

在 Web 中，你想要這樣做的情況特別常見。大部分我們所寫的 JavaScript 程式碼都是基於事件的 — 定義某種行為，然後將其新增到使用者觸發的事件之上（比如點選或者按鍵）。我們的程式碼通常作為回撥：為響應事件而執行的函式。

 

假如，我們想在頁面上新增一些可以調整字號的按鈕。一種方法是以畫素為單位指定 body 元素的 font-size，然後通過相對的 em 單位設定頁面中其它元素（例如header）的字號：

 

body {

font-family: Helvetica, Arial, sans-serif;

font-size: 12px;

}

 

h1 {

font-size: 1.5em;

}

 

h2 {

font-size: 1.2em;

}

我們的文字尺寸調整按鈕可以修改 body 元素的 font-size 屬性，由於我們使用相對單位，頁面中的其它元素也會相應地調整。

 

閉包，正則- 自動機-詞法分析器:

 

 

 

 

資料庫的關係和編譯原理的關係：

D1 D2 D3 笛卡爾積D1 x D2 x … Dn的子集合，記作R(D1, D2, … , Dn)

R稱為關係名，n為關係的目或度

編譯原理的關係：

其實應該差不多，D1 D2 D3代表的是語言或者串

D1 D2 D3 笛卡爾積D1 x D2 x … Dn的子集合，記作R(D1, D2, … , Dn)

R稱為關係名，n為關係的目或度

那麼編譯原理的閉包和js或者說java內部類的閉包有什麼一樣的呢

閉包在

數學中是閉的集合,也就是集合和它的邊界的並。

其實看起來不管是js編譯原理，java裡面的閉包都源自數學裡面這個閉包的概念。

編譯原理的閉包的概念其實是一個集合裡面連線N次，但是數學裡面是集合和邊界的並，其實要是畫一個圖理解起來是一樣的。 Js的閉包呢？

 

還有關係這個概念資料庫裡的關係，編譯原理裡面的關係應該都是脫胎於數學的關係或者二元關係https://baike.baidu.com/item/%E4%BA%8C%E5%85%83%E5%85%B3%E7%B3%BB/2587180?fr=aladdin

見百度百科二元關係的解釋。

https://blog.csdn.net/Jbinbin/article/details/84250852

見這個部落格 資料庫關係的解釋。

 

 

1. 正則表示式

為了描述程式設計語言所有合法的識別符號，界符 ，運算子,關鍵字，常數。

Letter表示任一字母或者下劃線

Digit表示數字

那麼識別符號可以用 letter_(letter_|digit)*  正則表示式表示。

正則表示式可以由較小的正則表示式按照如下規則遞迴地構建。

每個正則表示式r表示一個語言L（r），這個語言也是根據r的子表示式鎖表示的語言遞迴地定義的。

在某個字母表E 上的正則表示式以及這些表示式所表示的語言。

歸納基礎：  字母表用E表示，那個符號有點特殊，打不出，只好用E表示

1. E是一個正則表示式L（E）={E}，即該語言只包含空串。
2. 如果a是E上的一個符號，那麼a是一個正則表示式，並且L（a）={a}。也就是說，這個語言僅包含一個長度為1的符號串a。

下面我們舉例說明。對於符號集合∑={a，b}，有：

- 正則表示式a表示語言{a}；

- 正則表示式a|b表示語言{a，b}；

- 正則表示式(a|b)(a|b)表示語言{aa，ab，ba，bb}；

- 正則表示式a*表示語言{ε，a，aa，aaa，…}；

- 正則表示式(a|b)*表示語言{ε，a，b，aa，ab，ba，bb，aaa，…}；

- 正則表示式a|a*b表示語言{a，b，ab，aab，aaab，…}。

正則定義： 為方便表示，我們可能希望給某些正則表示式命名，並在之後的正則表示式中像符號一樣使用這些名字：  d1->r1  比如 digit ->{0-9} digits->digit+

圖3-11digit就是正則定義，右邊是正則表示式。

1. 每個d1都是一個新符號，他們都不在E中，並且各不相同。
2. 每個r都是字母表E  U {d1,d2,d3,d4..dn-1}的正則表示式。

1. 狀態轉換圖-確定的有窮自動機和不確定的又窮自動機

我們可以將正則表示式轉換成狀態轉換圖

初始狀態  接受狀態，終結狀態

Relop  關係運算符

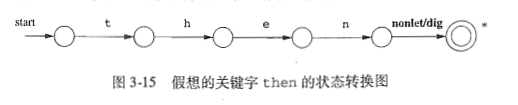
Digit表示式對應的狀態轉換圖：

 

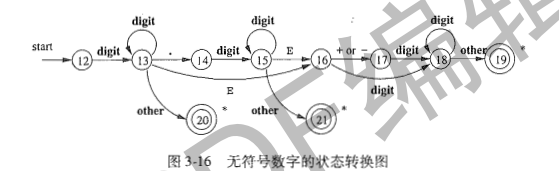
自動機：  有窮自動機是識別器，他們只能對每個可能的輸入串簡單的回答 “是”或者“否”。

1. 1. 不確定的有窮自動機，對齊邊上的標號沒有任何限制，一個符號標記離開同一狀態的多邊條。並且空串E也可以作為標號。
   2. 對於每個狀態及自動輸入字母表的每個符號，確定的有窮自動有且只有一條離開該狀態，以該符號為標號的邊。

 

 

 

不確定的有窮自動機：

   1一個有窮的狀態集合S

   2 一個輸入符號集合E 即輸入字母表，我們假設代表空串的E不是E中的元素

   3  一個轉換函式，他為每個狀態和E U {E}中的每個符號都給出了相應的後繼狀態的集合

   4 S中的一個狀態被S0被指定為開始狀態

   5  S的一個位元組F被指定為接受狀態集合

確定的有窮自動機

確定的有窮自動機（Deterministic Finite Automate，下文簡稱DFA）是NFA的一個特例，其中：

 

標記集合：一個輸入符號集合∑，但不包含空串ε；

轉換函式：對每個狀態s和每個輸入符號a，有且僅有一條標號為a的邊離開s，即轉換函式的對應關係從一對多變為了一對一。