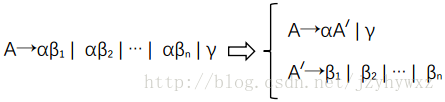詞法分析器把源程式轉換成了一個詞素序列，它讓我們知道了一個符號序列’i’、’f’是一個關鍵詞”if”，而一個符號序列’1’、’2’、’3’、’4’是一個常量”1234”等等。但是，詞法分析器的工作也到此為止了，它不能說明幾個詞素之間的關係。例如，對於詞素串”int”、”x”、”=”、”1”、”;”，詞法分析器不知道它是一個語句；對於詞素串”int”、”x”、”==”、”1”、”;”，詞法分析器不能檢測出它的語法錯誤。為此，在詞法分析之後，還需進行語法分析。

語法分析器的作用
我們都知道，在使用某一種程式設計編寫程式時，都要遵循一套特定的規則。比如，在C語言中，一個程式由多個函式組成，一個函式由宣告和語句組成，一個語句由表示式組成等等。這組規則精確描述了一個良構的程式設計語言的語法。語法分析器能夠確定一個源程式的語法結構，能夠檢測出源程式中的語法錯誤，並且能夠從常見的錯誤中恢復並繼續處理程式的其餘部分。

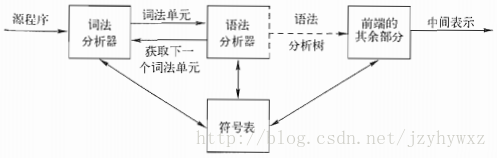
一個語法分析器從詞法分析器獲得一個詞素序列，並驗證這個序列是否可以由源語言的文法生成。語法分析器會構造一棵語法分析樹，並把它傳遞給編譯器的其他部分進一步處理，在構建語法分析樹的過程中，就驗證了這個詞素序列是否符合源語言的文法。語法分析器在編譯器中的位置如下圖：

文法
一個文法用於系統的描述程式設計語言的構造的語法。一個正確設計的文法給出了一個語言的結構，該結構有助於把源程式翻譯為正確的目的碼，也有助於檢測錯誤。

上下文無關文法
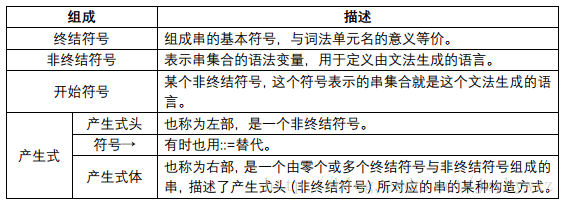
一個上下文無關文法（下文簡稱文法）由終結符號、非終結符號、一個開始符號和一組產生式組成：

對於產生式頭相同的兩個或多個產生式，可以把它們的產生式體用“|”連線寫成一個產生式。例如，對產生式E→E+T和E→T，可以寫成E→E+T|T。

一個貫穿全文的表示式文法
在進入主題之前，先給出一個簡單的表示式文法，把它稱為文法G，它將作為一個貫穿全文的例子：

    E→E+T|T
    T→T*F|F
    F→(E)|id
1
2
3
在文法G中，有3個產生式。其中，符號”+”、”*”、”(“、”)”、”id”是終結符號，符號”E”、”T”、”F”是非終結符號；符號E是開始符號，表示文法G可以生成的語言。

關於符號的約定
在下文中由於需要會出現大量的符號，為了減少冗餘和方便理解，我們在此對使用的符號有如下約定：

大寫字母表示非終結符號，如A、B、C等；
希臘字母表示任意由非終結符號和終結符號組成的串或者空串，如α、β、γ等。
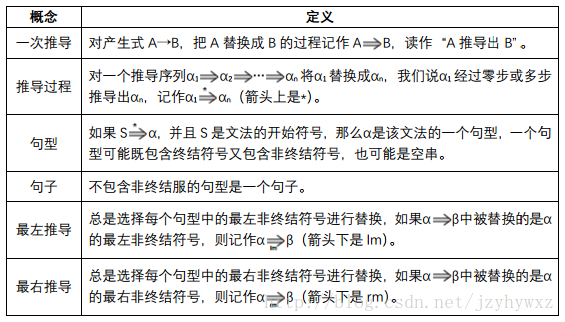
推導和規約
語法分析器在構建一棵語法分析樹時，常用的方法可以分為自頂向下和自底向上的。顧名思義，自頂向下的方法是從語法分析樹的根結點開始向葉子結點構造的方法，自底向上的方法是從語法分析樹的葉子結點開始向根結點構造的方法。在自頂向下的構造過程中，需要從一個非葉子結點“推導”出其子樹；在自底向上的構造中，需要把幾個非根結點“規約”成其根結點。

推導
從產生式的角度來看，一次推導過程是把產生式的左部替換成產生式的右部的過程。

對文法G，從E到id*id+id的一個最左推導和最右推導分別為：

其中，id*id+id是文法G的一個句子，其他中間步驟是文法G的句型。從此亦可看出，對相同句型的推導過程不唯一。

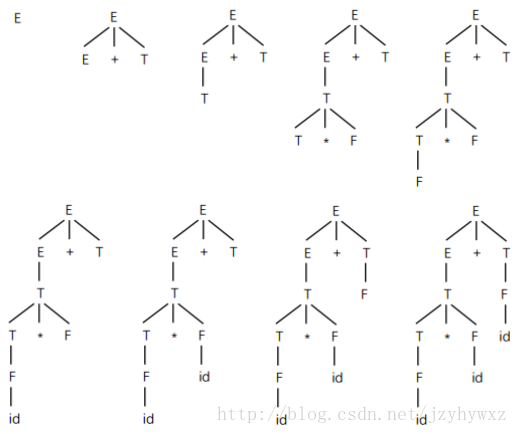
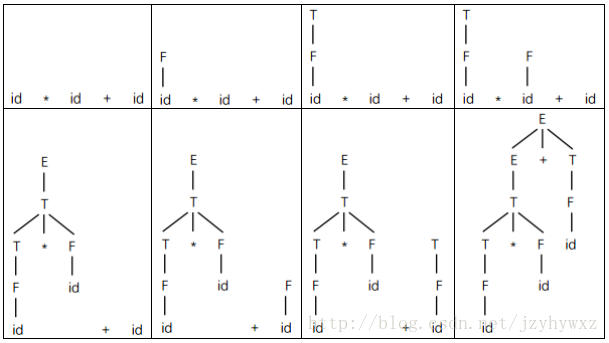
推導過程可以用語法分析樹表示，從E到id*id+id的最左推導的語法分析過程如下圖所示：

每棵語法分析樹對應於某一次推導，從左到右把語法分析樹的葉子結點連線起來就是文法G的一個句型，也稱為語法分析樹的結果或邊緣，最後一棵語法分析樹的葉子結點從左到右連線起來是文法G的一個句子。

規約
規約是推導的逆過程，一次規約是把一個與某產生式體相匹配的串替換為該產生式頭的非終結符號。

規約過程可以用於自底向上構造語法分析樹。例如，把id*id+id規約成E，這裡的每次規約是某次最右推導的逆過程，構造的語法分析樹如下圖所示：

設計文法
本節將介紹如何對一個文法進行轉換使其更適用於語法分析，這些轉換方法包括消除二義性，消除左遞迴和提取左公因子。

消除二義性
如果一個文法可以為某個句子生成多棵語法分析樹，那麼它就是二義性的，簡單地說，二義性文法就是對同一個句子有多個最左推導或多個最右推導的文法。

考慮下面的文法：

    E→E+E
    E→E*E
    E→(E)
    E→id
1
2
3
4
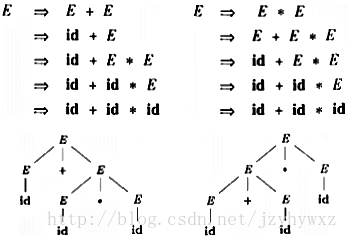
它對句子id+id*id有兩個最左推導，下圖給出了推導過程和相應的語法分析樹：

可以看出，這兩個推導過程反映了加法和乘法的優先順序問題，左邊的推導乘法優先順序比加法高，右邊的推導加法的優先順序比乘法高。實際上，左邊的推導過程更符合我們的觀念。

通過把該文法改寫成文法G的形式，可以解決這個二義性問題，該文法和文法G都生成同樣的語言。

消除左遞迴
如果一個文法對一個非終結符號A，經過一次或多次推導後得到串Aα，那麼這個文法是左遞迴的。如果該文法中存在形如A→Aα的產生式，則該產生式是立即左遞迴的。

在介紹消除文法的左遞迴之前，我們先介紹如何消除產生式的立即左遞迴。對任意立即左遞迴的產生式，可以用下面的方法消除立即左遞迴：

右邊的兩個產生式生成的串集合和左邊的產生式生成的串集合是相同的，並且右邊的兩個產生式沒有左遞迴，這樣就消除了產生式的左遞迴。

現在正式介紹對一個左遞迴的文法如何消除其左遞迴。對一個左遞迴的文法，用下面的方法消除左遞迴：

對文法G，消除它的左遞迴：

將非終結符號排序為E、T、F；
當i=1時，對符號E，產生式E→E+T|T是立即左遞迴的，把它替換為E→TE＇和E＇→+TE＇|ε；
當i=2時，對符號T，產生式T→T*F|F中沒有E，但它是立即左遞迴的，把它替換為T→FT＇和T＇→*FT＇|ε；
當i=3時，對符號F，產生式F→(E)|id中有E，把E替換為TE＇後得到F→(TE＇)|id，它不是立即左遞迴的，演算法結束；
最後得到的非左遞迴文法為：
    E→TE＇
    E＇→+TE＇|ε
    T→FT＇
    T＇→*FT＇|ε
    F→(TE＇)|id
1
2
3
4
5
提取左公因子
當使用自頂向下的方法構造語法分析樹時，如果在“展開”一個非終結符號的結點時，有不止一個產生式可以選擇，此時無法明確知道該使用哪一個產生式。為了解決這個問題，我們可以通過改寫產生式來推後這個決定，等獲得足夠的資訊後再做出正確的選擇。

例如，對於產生式A→+α|+β，假設α和β開頭的符號不同，當看到輸入“+”時，不能明確決定使用+α還是+β來替換A，只有繼續讀入下一個輸入，才能確定到底使用哪一個產生式。對此，可以把A→+α|+β轉換成A→+A＇和A＇→α|β，這樣當看到輸入“+”時，可以把A替換為A＇，再根據後續的輸入決定如何替換A＇。

對一個文法提取左公因子，對於每個非終結符號A，找出它的兩個或多個選項之間的最長公共字首α，如果α不是空串，那麼將所有頭為A的產生式做如下替換：

其中，γ表示所有不以α開頭的串，A＇是一個新的非終結符號。不斷應用這個轉換，直到每個非終結符號的任意兩個產生式體都沒有公共字首為止。
--------------------- 
作者：jzyhywxz 
來源：CSDN 
原文：https://blog.csdn.net/jzyhywxz/article/details/78392644 
版權宣告：本文為博主原創文章，轉載請附上博文連結！