【資料結構】資料結構糾錯本

標籤（空格分隔）：【考研糾錯本】

---

考研資料結構糾錯本

文章目錄

• 考研資料結構糾錯本
• 1 第一輪
• 1. 緒論
• 2. 線性表的基本概念與實現
• 3. 棧、佇列和多維陣列
• 4. 樹與二叉樹
• 5. 圖
• 6. 查詢
• 7. 排序
• 2 第二輪
• 1. 緒論
• 2. 線性表
• 3. 棧和佇列
• 4. 樹和二叉樹
• 5. 圖
• 6. 查詢
• 7. 排序
• 3. 第三輪
• 1. 線性表
• 2. 棧和佇列
• 3. 串
• 4. 陣列、矩、廣義表
• 5. 樹與二叉樹
• 6. 圖
• 7. 排序
• 8. 排序
• 4. 第四輪
• 1. 樹與二叉樹
• 2. 圖
• 2. 排序
• 3. 查詢
• 5. 第五輪
• 第1章. 概論
• 第2章. 線性表
• 我的微信公眾號

1 第一輪

1. 緒論

1. 對資料序列(8，9，10，4，5，6，20，1，2)採用(由後向前次序的)氣泡排序，需要進行的趟數(遍數)至少是（）
   A．3
   B．4
   C．5
   D．8
   答案： $C$

   C
   氣泡排序：它重複地走訪過要排序的元素列，依次比較兩個相鄰的元素，如果他們的順序錯誤就把他們交換過來。
   第一趟之後的序列： 1 8 9 10 4 5 6 20 2
   第二趟之後的序列： 1 2 8 9 10 4 5 6 20
   第三趟之後的序列： 1 2 4 8 9 10 5 6 20
   第四趟之後的序列： 1 2 4 5 8 9 10 6 20
   第五趟之後的序列： 1 2 4 5 6 8 9 10 20
   此時已經排好順序，因此答案為 至少 5 趟。

2. 以下哪個資料結構不是多型資料型別（）
   A.棧
   B.廣義表
   C.有向圖
   D.字串
   答案： $D$

   D
   多型資料型別就是資料元素的型別不確定。字串中每個元素始終是字元，不會是別的型別。

2. 線性表的基本概念與實現

1. 設線性表非空，採用下列__________所描述的連結串列可以在 $O(1)$時間內在表尾插入一個新結點。
   A. 帶表頭結點的單鏈表，一個連結串列指標指向表頭結點
   B. 帶表頭結點的單迴圈連結串列，一個連結串列指標指向表頭結點
   C. 不帶表頭結點的單鏈表，一個連結串列指標指向標的第一個結點
   D. 不帶表頭結點的單迴圈連結串列，一個連結串列指標指向表的第一個節點
   答案： $B$
   在表尾插入一個結點，現在表頭後新增一個新表頭，再把原表頭轉換為一個新的結點。

2. 假定採用帶頭結點的單鏈表儲存單詞，當兩個單詞有相同的字尾時，則可共享相同的字尾儲存空間。
   例如，“loading”和“being”的儲存映像如下圖所示。
   
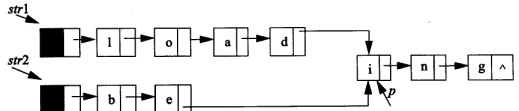
   設str1和str2分別指向兩個單詞所在單鏈表的頭結點，連結串列結點結構為。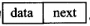
   請設計一個時間上儘可能高效的演算法，找出由str1和str2所指的兩個連結串列共同字尾的起始位置(如圖中字元i所在結點的位置p)。
   要求： (1)給出演算法的基本設計思想。 (2)根據設計思想，採用C或C++或Java語言描述演算法，關鍵之處給出註釋。 (3)說明你所設計演算法的時間複雜度。
   解答：

3. 基本思想：1> 分別求出 str1 和 str2 所指的兩個連結串列的長度 l1 和 l2. 2> 將兩個連結串列表尾對齊：令指標 p, q 分別指向 str1 和 str2 的頭節點。如果 l1 > l2 ，那麼令 p 指向連結串列中的第 l1 - l2 + 1 個結點；如果 l1 < l2，那麼令 q 指向連結串列中的第 l2 - l1 + 1 個結點；如果 l1 == l2 那麼 p和 q 所指的結點到尾部的長度相等。 3> 反覆將 p 和 q 進行比較，如果不相等則同時後移，當 p 和 q 指向同一個結點時，該結點便是共同字尾的起始位置。

typedef struct Node{
       char data;
       struct Node *next;
}SNode;

SNode *FindSame(SNode *str1, SNode *str2){
       int l1, l2;
       SNode *p,*q;
       p = str1->next; q = str2->next;
       int l1,l2; l1 = l2 = 0;
       while( p){
           l1++;p=p->next;
       }
       while( q){
           l2++;q=q->next;
       }
       p = str1->next; q = str2->next;
       if( l1 > l2)
           for( int i = 0; i < l1 - l2; i++)
               p = p->next;
       else if( l1 < l2)
           for( int i = 0; i < l2 - l1; i++)
               q = q->next;
       //compare
       while( p && p->data != q->data){
           p = p->next;
           q = q->next;
       }
       return p;
}

3. 時間複雜度： $O(m+n)$

4. 在順序表的動態儲存定義中需要包含的資料成員是（）
   I. 陣列指標 $~~~~~~~~~~~~~~~$II. 表中元素個數n
   III. 表的大小maxSize $~~~~~~$ IV. 陣列基址base
   A. I 、II
   B. I 、II、IV
   C. I 、II、III
   D. 全部
   答案： $C$
   在順序表的動態定義中，儲存空間通過執行 malloc 或者 new 動態分配，所以不需要陣列基址。

3. 棧、佇列和多維陣列

1. 若一個棧的輸入序列為1，2，3，…，n，輸出序列的第一個元素是i，則第j個輸出元素是______。
   A．i-j-1
   B．i-j
   C．j-i+1
   D．不確定
   答案： $D$
   i出棧時，1，2…i-1 都在棧內，但是不排除 i + 1之後的元素進棧。因此不確定。

2. 對於鏈式佇列，在執行入隊操作時（）
   A. 僅需修改頭指標
   B. 僅需修改尾指標
   C. 頭、尾指標都需要修改
   D. 頭、尾指標可能都要修改
   答案： $D$
   對於鏈式佇列，一般而言只需要修改尾指標。但是當向 空佇列 入隊時，隊頭指標和隊尾指標均需要修改。

3. 最適合用做鏈式佇列的連結串列是______。
   A.帶有隊頭指標和隊尾指標的迴圈單鏈表
   B.帶有隊頭指標和隊尾指標的非迴圈單鏈表
   C.只帶隊頭指標的迴圈單鏈表
   D.只帶隊頭指標的非迴圈單鏈表
   答案： $B$
   由於佇列需要在雙端進行操作，所以只有 隊首指標 不合適。A，迴圈連結串列有些多餘。

4. 是否可以用兩個棧模擬一個佇列？反之，是否可以用兩個佇列模擬一個棧?
   答案：兩個棧可以模擬一個佇列，但是兩個佇列不能模擬一個棧。
   棧是一種先進後出的資料結構，可以使用一個棧把一個輸入序列逆轉，然後使用另外一個棧把逆轉後的序列再逆轉回來。
   但是兩個佇列不能模擬一個棧。（存疑？）

5. 判斷：鏈式棧的棧頂指標一定指向棧的棧尾。
   答案： $錯誤$
   鏈式棧一般採用單鏈表，棧頂指標為頭指標。進棧出棧均在鏈頭進行。

6. 已知迴圈佇列儲存在一維陣列A[0．n-1]中，且佇列非空時front和rear分別指向隊頭元素和隊尾元素。若初始時佇列為空，且要求第1個進入佇列的元素儲存在A[0]處，則初始時front和rear的值分別是（）
   A．0， 0
   B．0， n-1
   C．n-1，0
   D．n-1，n-1
   答案： $B$
   在迴圈佇列中，進隊操作是隊尾指標rear +1 ,並在該位置放置進隊的元素，而隊首指標不變。
   在本題中，要求第一個進隊元素放在A[0]處，佇列非空時front 和 rear 分別指向隊頭和隊尾元素，此時要求fornt和rear均為0。因此，初始時候rear應該為n-1，而front 應該為0.

7. 隊列出隊時，當佇列中多餘一個節點時，僅僅需要修改隊頭指標。但如果佇列中只剩下一個節點時，此時出隊，隊首、隊尾指標都需要修改為NULL.

8. 用十字連結串列表示一個稀疏矩陣，每個非零元一般用一個含有 （ ） 個域的結點表示。
   A．2
   B．3
   C．4
   D．5
   答案： $D$
   儲存稀疏句真的十字連結串列節點包含 5 個域：該非零元的行下標，該非零元的列下標，該非零元所在行表的後繼鏈域，該非零元所在列表的後繼鏈域。

4. 樹與二叉樹

1. 已知三叉樹T中6個葉結點的權分別是2，3，4，5，6，7，T的帶權(外部)路徑長度最小是（）
   A．27
   B．46
   C．54
   D．56
   答案： $B$
   這道題考察哈夫曼樹的構造。

2. 已知一棵完全二叉樹的第 6 層（設根為第 1 層）有 8 個葉結點，則完全二叉樹的結點個數最多是 ()。
   A. 39
   B. 52
   C. 111
   D. 119
   答案： $C$
   第六層有 8個葉節點，則該完全二叉樹最多有 7 層，依照這個思路計算即可。

3. 若一棵完全二叉樹有768個結點，則該二叉樹中葉結點的個數是（）
   A.257
   B.258
   C.384
   D.385
   答案： $C$
   $n0+n1+n2+n3 = 768, ~~ 0 * n0 + 1 * n1 + 2* n2 +1 = 768 $
   完全二叉樹一個特點：當結點總數為奇數時，n1 = 0；當結點總數為偶數時，n1 = 1.
   對於題目中的二叉樹，n1=1,n0=384.

4. 已知一棵有2011個結點的樹,其葉結點個數為116，該樹對應的二叉樹無右孩子的結點個數為（）
   A. 115
   B. 116
   C. 1895
   D. 1896
   答案： $D$

5. 按照二叉樹的定義，具有三個結點的二叉樹有（）種形態。
   A. 6
   B. 5
   C. 4
   D. 3
   答案： $B$
   兩層有一種情況，三層有 4種情況，無需考慮data.

6. 當一棵有n個結點的二叉樹按層次從上到下，同層次從左到右將資料存放在一維陣列 A[l…n]中時，陣列中第i個結點的左孩子為( )
   A. A[2i](2i=<n)
   B. A[2i+1](2i+1= < n)
   C. A[i/2]
   D. 無法確定
   答案： $D$
   只有 完全二叉樹才可以可以確定左右孩子結點的位置。

7. 利用二叉連結串列儲存樹,則根結點的右指標是()
   A. 指向最左孩子
   B. 指向最右孩子
   C. 空
   D. 非空
   答案： $C$
   二叉連結串列儲存樹，首先需要將樹轉換為二叉樹。根據孩子兄弟表示法，由於樹的根結點一定沒有右兄弟，因此根節點一定沒有右孩子。即根節點的右指標為空。

8. 二叉樹的帶權路徑長度(WPL)是二叉樹中所有葉結點的帶權路徑長度之和。給定一棵二叉樹T，採用二叉連結串列儲存，結點結構為：
   
   其中葉結點的weight域儲存該結點的非負權值。設root為指向T的根結點的指標，請設計求T的WPL的演算法。
   要求：
   （1）給出演算法的基本設計思想；
   （2）使用C或C++語言，給出二叉樹結點的資料型別定義；
   （3）根據設計思想，採用C或C++語言描述演算法，關鍵之處給出註釋。
   答案：1. 演算法設計思想：遞迴遍歷二叉樹，利用同一個引數對深度進行記數。
   葉節點的WPL = 該結點的weight * 深度。
   二叉樹的WPL = 樹中全部 葉節點 的帶權路徑長度之和 = 根節點左子樹全部葉節點的帶權路徑之和 + 根節點右子樹全部葉節點的帶權路徑之和。

typedef struct BTnode{
      unsigned int weight;
      struct BTnode *lchild, *lchild;
}BTnode;

int main(){
       return WPL( root, 0);
}

int WPL( BTnode *root, int d){
   if( root->lchild == NULL && root->rchild == NULL)
       return (root->weight  *d);
   else
       return WPL(root->lchild, d+1) + WPL(root->rchild, d+1);
}

9. 對於二叉樹的兩個結點X和Y，應該選擇（ ） 兩個序列來判斷X是否為Y的祖先。
   A．先序和後序
   B．先序和中序
   C．中序和後序
   D．任意兩個序列都行
   答案： $D$
   任意兩個排序都可以判斷 X 是不是 Y 的祖先。
   但是，先序和後序無法得到二叉樹的結構，但是可以判斷祖先。

10. 若二叉樹採用二叉連結串列儲存結構，要交換其所有分支結點左、右子樹的位置，利用（）遍歷方法最合適。
    A．前序
    B．中序
    C．後序
    D．按層次
    答案： $C$
    如果交換所有分支結點左右子樹，可以遞迴地操作：先交換左子數中所有分支結點，再遞迴交換右子樹中所有分支結點。最後對根節點交換其子樹位置。如此先左後右再根節點的方式為 後序遍歷。

11. 將一棵二叉樹轉化成森林，可按如下步驟進行：
    ① 抹線：將二叉樹根結點與其右孩子之間的連線，以及沿著此右孩子的右鏈連續不繼搜尋到的右孩子間的連線抹掉。這樣就得到了若干棵根結點沒有右子樹的二叉樹。
    ② 將得到的這些二叉樹用前述方法分別轉化成一般樹。

12. 能唯一確定原二叉樹的遍歷方式組合為：前序 + 中序，或者 後序 + 中序，注意，前序遍歷加後序遍歷不可以唯一確定二叉樹。

13. 二叉樹線上索化後,仍不能有效求解的問題是()
    A. 前序線索二叉樹中求前序後繼
    B. 中序線索二叉樹中求中序後繼
    C. 中序線索二叉樹中求中序前驅
    D. 後序線索二叉樹中求後序後繼
    答案： $D$
    中序線索二叉樹 無論是求 中序後繼 還是求 中序前驅店鋪可以較好解決。
    先序線索二叉樹中查詢結點的 後繼 比較容易，但是查詢結點的前去要知道其雙親的資訊，要使用棧，因此說先序線索二叉樹是不完善的。
    後序線索二叉樹查詢結點的 前驅 比較容易，但是查詢結點的後繼需要知道其雙親結點的資訊，要 使用棧 ，因此說後序線索二叉樹是不完善的。

14. 線上索二叉樹中，下面說法不正確的是( )
    A. 在中序線索樹中，若某結點有右孩子，則其後繼結點是它的右子樹的左支末端結點。
    B.線索二叉樹是利用二叉樹的n+1 個空指標來存放結點前驅和後繼資訊的。
    C.每個結點通過線索都可以直接找到它的前驅和後繼
    D.在中序線索樹中，若某結點有左孩子，則其前驅結點是它的左子樹的右支末端結點。
    答案： $c$
    並不是每個結點都可以通過線索來直接找到它的前驅和後去。

15. 樹的遍歷 和 森林的遍歷 與 二叉樹遍歷的對應關係
    |樹|森林|二叉樹|
    |-----|
    |先根遍歷|先序遍歷|先序遍歷
    |後根遍歷|中序遍歷|中序遍歷

16. 將森林F轉換為對應的二叉樹T，F中葉結點的個數等於 （）
    A. T中葉結點的個數
    B. T中度為1的結點個數
    C. T中左孩子指標為空的結點個數
    D. T中右孩子指標為空的結點個數
    答案： $C$
    森林F 中的葉子結點對應二叉樹T中，沒有左孩子的結點。

17. 若平衡二叉樹的高度為6，且所有非葉結點的平衡因子均為 1，則該平衡二叉樹的結點總數為（ ）。
    A. 12
    B. 20
    C. 32
    D. 33
    答案： $B$
    平衡二叉樹中，假設用 $N_h$表示深度為h的平衡樹中含有的 最少 節點數，則滿足， $N_h = N_{h-1}+N_{h-2} + 1$, $N_0=0,N_1=1,N_2=2$.
    還可以證明，含有n個節點的平衡二叉樹的最大深度為 $O(log_2n)$

18. 對二叉排序樹進行_________遍歷可以得到結點的排序序列。
    A．前序
    B．中序
    C．後序
    D．層次
    答案： $B$

19. 折半搜尋與二叉排序樹的時間效能（ ）。
    A．相同
    B．完全不同
    C．有時不相同
    D．數量級都是O(log2n)
    答案： $C$

20. 查詢效率最高的二叉排序樹是______。
    A．所有結點的左子樹都為空的二叉排序樹
    B．所有結點的右子樹都為空的二叉排序樹
    C．平衡二叉樹
    D．沒有左子樹的二叉排序樹
    答案： $C$

5. 圖

1. 設有6個結點的無向圖，該圖至少應有（）條邊，才能確保是一個連通圖？
   A. 8
   B. 11
   C. 6
   D. 5
   答案： $B$
   注意題目中 “確保” 的含義，它意味著 無論六個頂點如何連線，都找不出非連通的情況。
   5 個頂點的完全圖需要10條邊，再加入一個頂點，第六個頂點無論怎麼連線都是連通的。共需11條邊。

2. 以下關於圖的敘述中，正確的是（）
   A．強連通有向圖的任何頂點到其他所有頂點都有弧
   B．圖的任意頂點的入度等於出度
   C．有向完全圖一定是強連通有向圖
   D．有向圖的邊集的子集和頂點集的子集可構成原有向圖的子圖
   答案： $C$
   D，假如選擇了某個邊，但是沒有選擇該邊的兩個頂點，便無法構成圖。

3. 要連通具有n個頂點的有向圖,至少需要（）條邊
   A. n-1
   B. n
   C. n+1
   D. 2n
   答案： $B$
   構成一個環即可。

4. G是一個非連通無向圖，共有28條邊，則該圖至少有（） 個頂點。
   A. 8
   B. 9
   C. 10
   D. 11
   答案： $B$
   8 個頂點連通圖無向圖最多有 28 個邊，若需要保持非連通，則需要 9 個頂點。

5. 對鄰接表的敘述中，（）是正確的。
   A．無向圖的鄰接表中，第i個頂點的度為第i個連結串列中結點數的兩倍
   B．鄰接表比鄰接矩陣的操作更簡便
   C．鄰接矩陣比鄰接表的操作更簡便
   D．求有向圖結點的度，必須遍歷整個鄰接表
   答案： $D$
   A，無向圖的鄰接表，第 i 個頂點的度為第 i 個連結串列中結點數的一倍。
   B，C，好比“線性表中鏈式儲存和順序儲存的優劣”一樣。

6. 若鄰接表中有奇數個邊表結點，則一定是（）
   A．圖中有奇數個結點
   B．圖中有偶數個結點
   C．圖為無向圖
   D．圖為有向圖
   答案： $D$
   無向圖的鄰接表中結點數為邊數的兩倍。

7. 深度優先搜尋可以利用遞迴的方法，使用堆疊作為輔助空間。
   廣度優先搜尋利用佇列作為輔助空間。

8. 一個 n 個結點和 e 條邊的圖。
   |儲存結構| 遍歷方式|時間複雜度|空間複雜度|
   |----|-----|----|
   |鄰接表 |深度優先遍歷| $O(n+e)$| $O(n)$
   |鄰接矩陣 |深度優先遍歷| $O(n^2)$| $O(n)$
   |鄰接表 |廣度優先遍歷| $O(n+e)$| $O(n)$
   |鄰接矩陣 |廣度優先遍歷| $O(n^2)$| $O(n)$

9. 下面演算法中可以判斷出一個有向圖是否有環的是：（）
   A. 求最短路徑
   B. 深度優先遍歷
   C. 廣度優先遍歷
   D. 拓撲排序
   答案： $BD$
   深度優先遍歷，對每一個點標記，如果訪問到已經標記的點則說明存在迴路。
   拓撲排序，對於入度為0的結點使之讓入隊，然後讓該點所有相連線的點入度減1，重複n-1次後，如果還有點沒有進入輸出佇列，則這些點在環上。

10. 圖的BFS生成樹的樹高比DFS生成樹的樹高()
    A. 小或相等
    B. 小
    C. 大或相等
    D. 大

11. 若一個有向圖具有有序的拓撲排序序列，那麼它的鄰接矩陣必定為（）。
    A．對稱矩陣
    B．稀疏矩陣
    C．三角矩陣
    D．一般矩陣
    答案： $D$
    一個有向圖具有拓撲排序序列，說明它是一個有向無環圖（DAG），但是DAG圖在鄰接矩陣上沒有直接的表示。為一般矩陣。

12. 一個 n 個結點和 e 條邊的圖。

    功能	演算法	時間複雜度
    最小生成樹	Prim普里姆	$O(n^2)$