從深入淺出理解決策樹演算法（一）-核心思想 - 知乎專欄文章中，我們已經知道了決策樹最基本也是最核心的思想。那就是其實決策樹就是可以看做一個if-then規則的集合。我們從決策樹的根結點到每一個都葉結點構建一條規則。

並且我們將要預測的例項都可以被一條路徑或者一條規則所覆蓋。

如下例：假設我們已經構建好了決策樹，現在買了一個西瓜，它的特點是紋理是清晰，根蒂是硬挺的瓜，你來給我判斷一下是好瓜還是壞瓜，恰好，你構建了一顆決策樹，告訴他，沒問題，我馬上告訴你是好瓜，還是壞瓜？

根據決策樹的演算法步驟，我們可以得到下面的圖示過程：

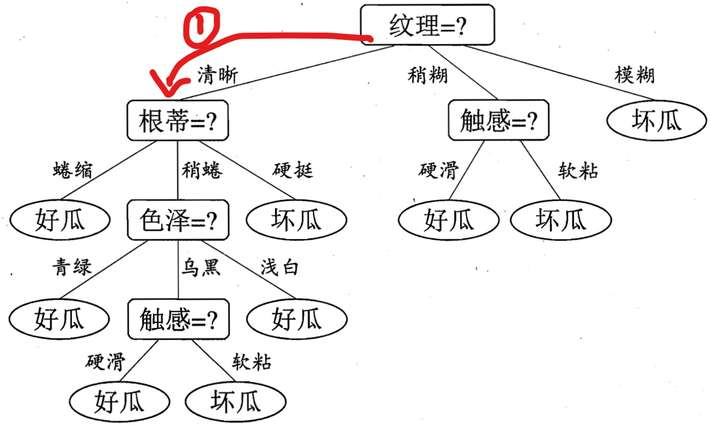
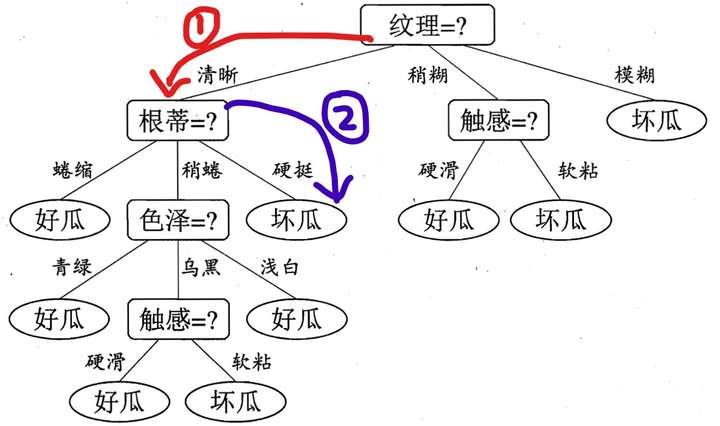
到達葉子結點後，從而得到結論。我這個瓜的判斷是壞瓜。

演算法思路在上篇文章都講解過，這裡我們重點來說一下，在每一層的生長過程中，如何選擇特徵！每一層選擇好了特徵之後，樹也就自然建好了。

決策樹學習的關鍵其實就是選擇最優劃分屬性，希望劃分後，分支結點的“純度”越來越高。那麼“純度”的度量方法不同，也就導致了學習演算法的不同，這裡我們講解最常見的倆種演算法，ID3演算法與C4.5演算法。

ID3演算法

我們既然希望劃分之後結點的“純度”越來越高，那麼如何度量純度呢？

“資訊熵”是度量樣本集合不確定度（純度）的最常用的指標。

在我們的ID3演算法中，我們採取資訊增益這個量來作為純度的度量。我們選取使得資訊增益最大的特徵進行分裂！那麼資訊增益又是什麼概念呢？

我們前面說了，資訊熵是代表隨機變數的複雜度（不確定度）通俗理解資訊熵 - 知乎專欄，條件熵代表在某一個條件下，隨機變數的複雜度（不確定度）通俗理解條件熵 - 知乎專欄。

而我們的資訊增益恰好是：資訊熵-條件熵。

我們看如下定義：

•當前樣本集合 D 中第 k 類樣本所佔的比例為 pk ，則 D 的資訊熵定義為

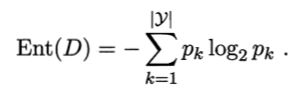
•離散屬性 a 有 V 個可能的取值 {a1,a2,…,aV}；樣本集合中，屬性 a 上取值為 av 的樣本集合，記為 Dv。

•用屬性 a 對樣本集 D 進行劃分所獲得的“資訊增益”

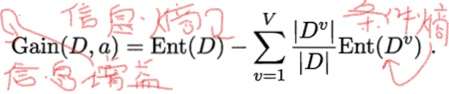
•資訊增益表示得知屬性 a 的資訊而使得樣本集合不確定度減少的程度

那麼我們現在也很好理解了，在決策樹演算法中，我們的關鍵就是每次選擇一個特徵，特徵有多個，那麼到底按照什麼標準來選擇哪一個特徵。

這個問題就可以用資訊增益來度量。如果選擇一個特徵後，資訊增益最大（資訊不確定性減少的程度最大），那麼我們就選取這個特徵。

好的，我們現在已經知道了選擇指標了，就是在所有的特徵中，選擇資訊增益最大的特徵。那麼如何計算呢？看下面例子：

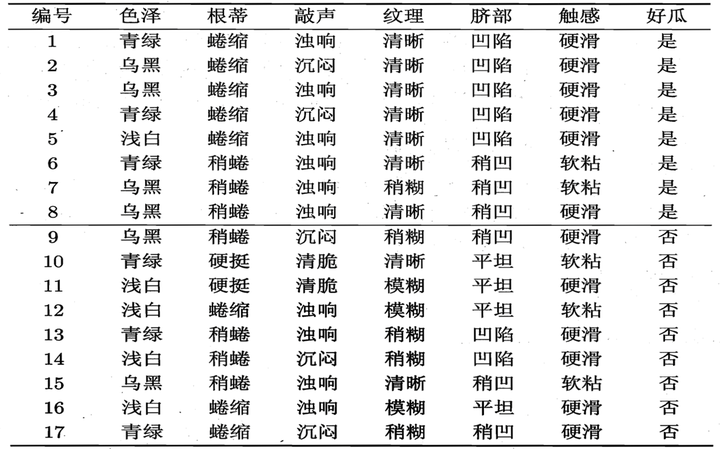
正例(好瓜)佔 8/17，反例佔 9/17 ，根結點的資訊熵為

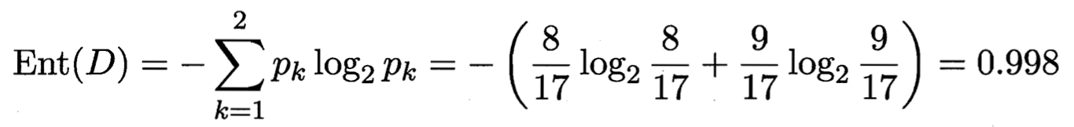
計算當前屬性集合{色澤，根蒂，敲聲，紋理，臍部，觸感}中每個屬性的資訊增益



色澤有3個可能的取值：{青綠，烏黑，淺白}

D1(色澤=青綠) = {1, 4, 6, 10, 13, 17}，正例 3/6，反例 3/6

D2(色澤=烏黑) = {2, 3, 7, 8, 9, 15}，正例 4/6，反例 2/6

D3(色澤=淺白) = {5, 11, 12, 14, 16}，正例 1/5，反例 4/5

3 個分支結點的資訊熵

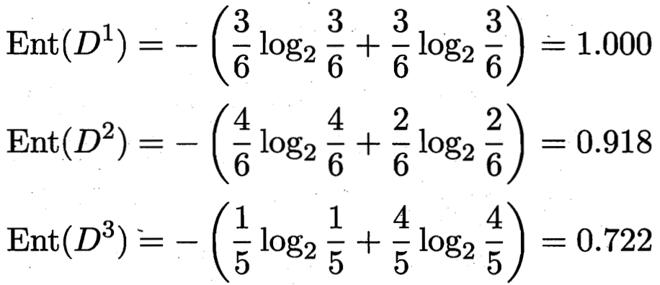
那麼我們可以知道屬性色澤的資訊增益是：

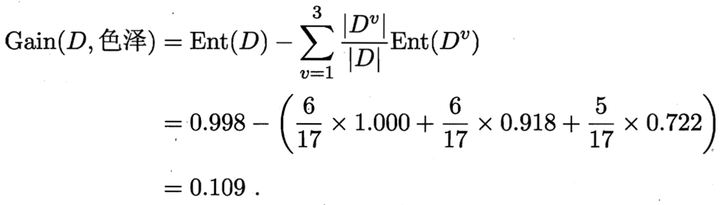
同理，我們可以求出其它屬性的資訊增益，分別如下：

於是我們找到了資訊增益最大的屬性紋理，它的Gain(D，紋理) = 0.381最大。
於是我們選擇的劃分屬性為“紋理”
如下：

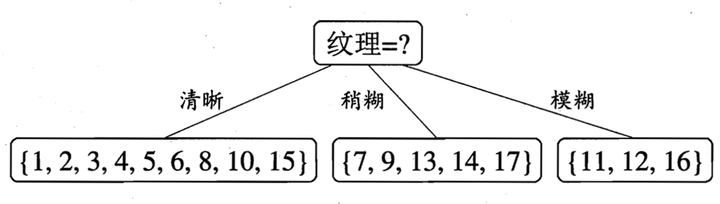
於是，我們可以得到了三個子結點，對於這三個子節點，我們可以遞迴的使用剛剛找資訊增益最大的方法進行選擇特徵屬性，
比如：D1(紋理=清晰) = {1, 2, 3, 4, 5, 6, 8, 10, 15}，第一個分支結點可用屬性集合{色澤、根蒂、敲聲、臍部、觸感}，基於 D1各屬性的資訊增益，分別求的如下：

於是我們可以選擇特徵屬性為根蒂，臍部，觸感三個特徵屬性中任選一個（因為他們三個相等並最大），其它倆個子結點同理，然後得到新一層的結點，再遞迴的由資訊增益進行構建樹即可
我們最終的決策樹如下：

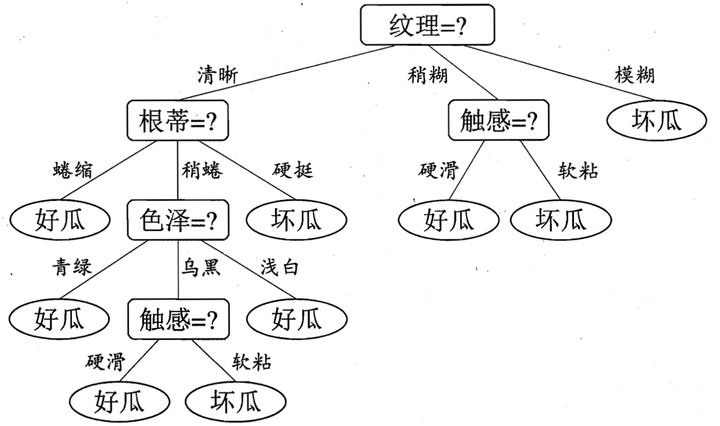
啊，那到這裡為止，我們已經知道了構建樹的演算法，上面也說了有了樹，我們直接遍歷決策樹就能得到我們預測樣例的類別。那麼是不是大功告成了呢？
結果是：不是的

我們從上面求解資訊增益的公式中，其實可以看出，資訊增益準則其實是對可取值數目較多的屬性有所偏好！
現在假如我們把資料集中的“編號”也作為一個候選劃分屬性。我們可以算出“編號”的資訊增益是0.998
因為每一個樣本的編號都是不同的（由於編號獨特唯一，條件熵為0了，每一個結點中只有一類，純度非常高啊），也就是說，來了一個預測樣本，你只要告訴我編號，其它特徵就沒有用了，這樣生成的決策樹顯然不具有泛化能力。


於是我們就引入了資訊增益率來選擇最優劃分屬性！

 

C4.5演算法

這次我們每次進行選取特徵屬性的時候，不再使用ID3演算法的資訊增益，而是使用了資訊增益率這個概念。

首先我們來看資訊增益率的公式：

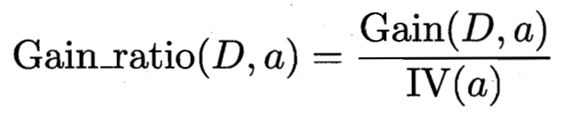
由上圖我們可以看出，資訊增益率=資訊增益/IV(a),說明資訊增益率是資訊增益除了一個屬性a的固有值得來的。

我們一開始分析到，資訊增益準則其實是對可取值數目較多的屬性有所偏好！（比如上面提到的編號，可能取值是例項個數，最多了，分的類別越多，分到每一個子結點，子結點的純度也就越可能大，因為數量少了嘛，可能在一個類的可能性就最大）。

但是剛剛我們分析到了，資訊增益並不是一個很好的特徵選擇度量。於是我們引出了資訊增益率。

我們來看IV(a)的公式：

屬性a的固有值：

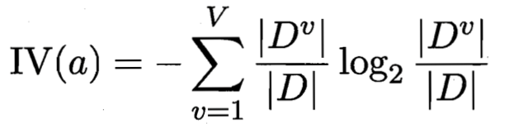
IV(觸感) = 0.874 ( V = 2 )

IV(色澤) = 1.580 ( V = 3 )

IV(編號) = 4.088 ( V = 17 

由上面的計算例子，可以看出IV(a)其實能夠反映出，當選取該屬性，分成的V類別數越大，IV(a)就越大，如果僅僅只用資訊增益來選擇屬性的話，那麼我們偏向於選擇分成子節點類別大的那個特徵。

但是在前面分析了，並不是很好，所以我們需要除以一個屬性的固定值，這個值要求隨著分成的類別數越大而越小。於是讓它做了分母。這樣可以避免資訊增益的缺點。

那麼資訊增益率就是完美無瑕的嗎？

當然不是，有了這個分母之後，我們可以看到增益率準則其實對可取類別數目較少的特徵有所偏好！畢竟分母越小，整體越大。

於是C4.5演算法不直接選擇增益率最大的候選劃分屬性，候選劃分屬性中找出資訊增益高於平均水平的屬性（這樣保證了大部分好的的特徵），再從中選擇增益率最高的（又保證了不會出現編號特徵這種極端的情況）希望對大家有幫助~

參考：

周志華《機器學習》，例子來源於書籍

德川《全體機器學習會slides》，很多都是總結於ppt

致謝：

德川，宇軒師兄

釋出於 2017-05-08