用R語言進行方差分析
阿新 • • 發佈:2018-12-24
R語言中與方差分析有關的包有car、gplots、HH、rrcov、multicomp、effects、MASS和mvoutlier。
單因素方差分析
#運用multcomp包中的cholesterol資料 library(multcomp) attach(cholesterol) #檢視療法特徵變數 table(trt) trt 1time 2times 4times drugD drugE 10 10 10 10 10 #檢視各組的均值以及方差 aggregate(response,by=list(trt),FUN=mean) Group.1 x 1 1time 5.78197 2 2times 9.22497 3 4times 12.37478 4 drugD 15.36117 5 drugE 20.94752 aggregate(response,by=list(trt),FUN=sd) Group.1 x 1 1time 2.878113 2 2times 3.483054 3 4times 2.923119 4 drugD 3.454636 5 drugE 3.345003 #檢驗組間差異(ANOVA) fit <- aov(response ~ trt) summary(fit) #這裡顯著說明組間存在差異 Df Sum Sq Mean Sq F value Pr(>F) trt 4 1351.4 337.8 32.43 9.82e-13 *** Residuals 45 468.8 10.4 --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 #繪製組間差異以及置信區間 library(gplots) plotmeans(response ~ trt, xlab = "Treatment", ylab = "Response", main = "Mean Plot \nwith 95% CI") detach(cholesterol)
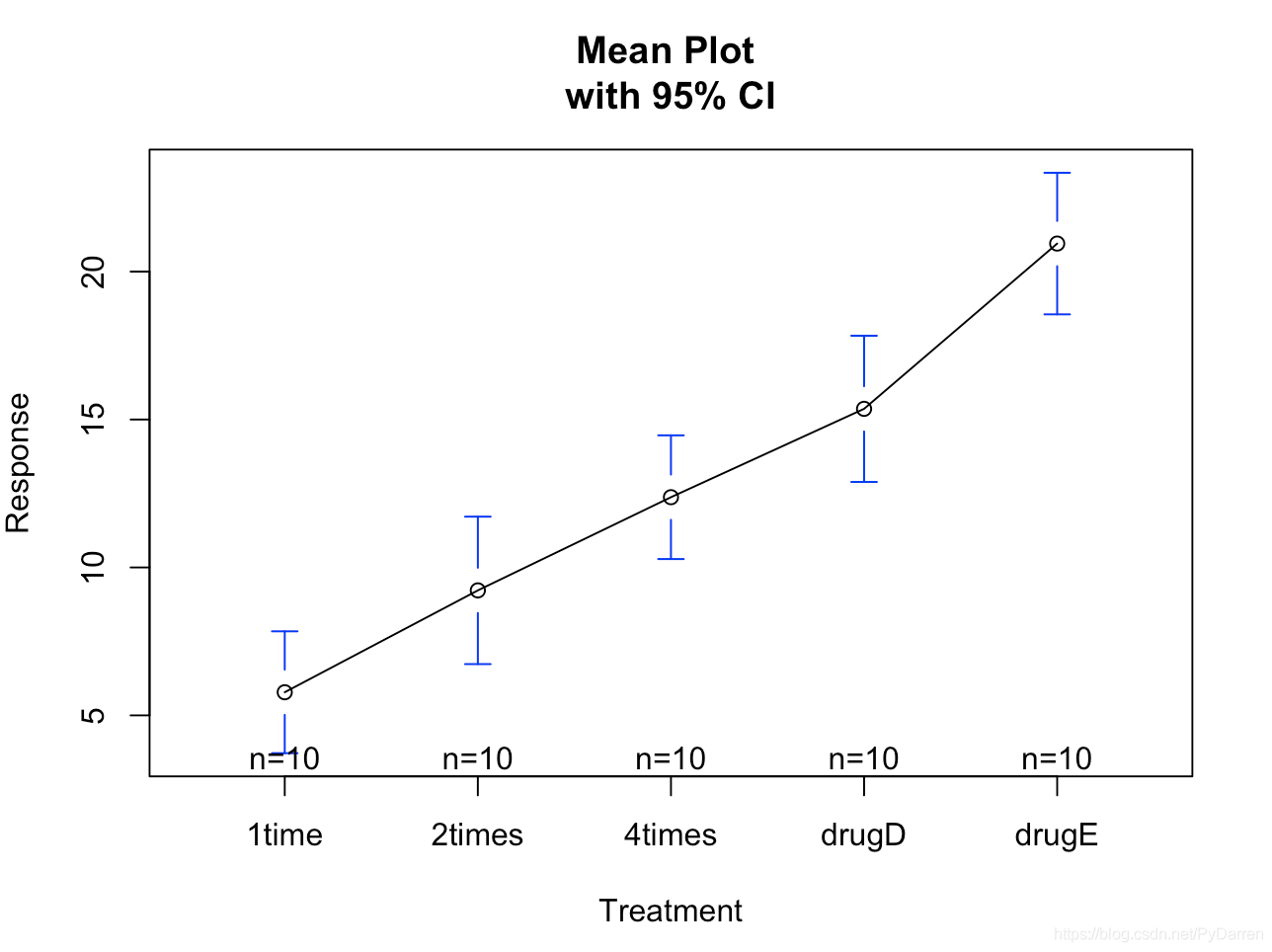
雖然ANOVA對各種療法的F檢驗證明其效果不同,但並不知道哪種療法與哪種療法之間不同。多重比較可以解決這個問題,利用TukeyHSD()函式可以對各組均值差異成對檢驗。
#對各組均值差異進行成對檢驗 TukeyHSD(fit) Tukey multiple comparisons of means 95% family-wise confidence level Fit: aov(formula = response ~ trt) $trt diff lwr upr p adj 2times-1time 3.44300 -0.6582817 7.544282 0.1380949 4times-1time 6.59281 2.4915283 10.694092 0.0003542 drugD-1time 9.57920 5.4779183 13.680482 0.0000003 drugE-1time 15.16555 11.0642683 19.266832 0.0000000 4times-2times 3.14981 -0.9514717 7.251092 0.2050382 drugD-2times 6.13620 2.0349183 10.237482 0.0009611 drugE-2times 11.72255 7.6212683 15.823832 0.0000000 drugD-4times 2.98639 -1.1148917 7.087672 0.2512446 drugE-4times 8.57274 4.4714583 12.674022 0.0000037 drugE-drugD 5.58635 1.4850683 9.687632 0.0030633 #進行視覺化 par(las=2) #旋轉軸標籤 par(mar=c(5,8,4,2)) #增大左邊界的面積 plot(TukeyHSD(fit))
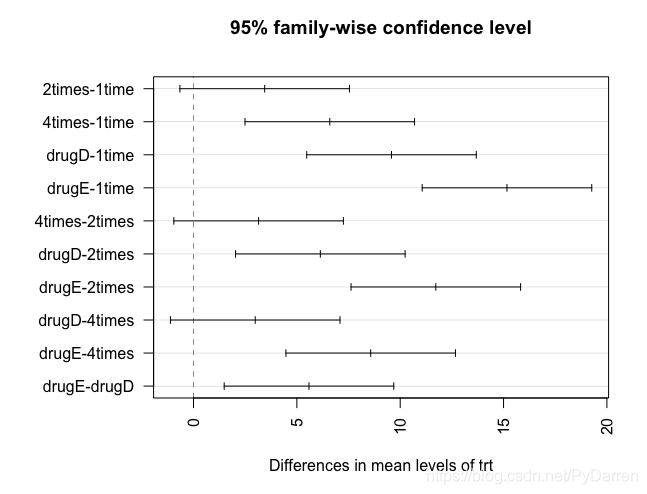
其中置信區間包含0說明差異並不顯著。
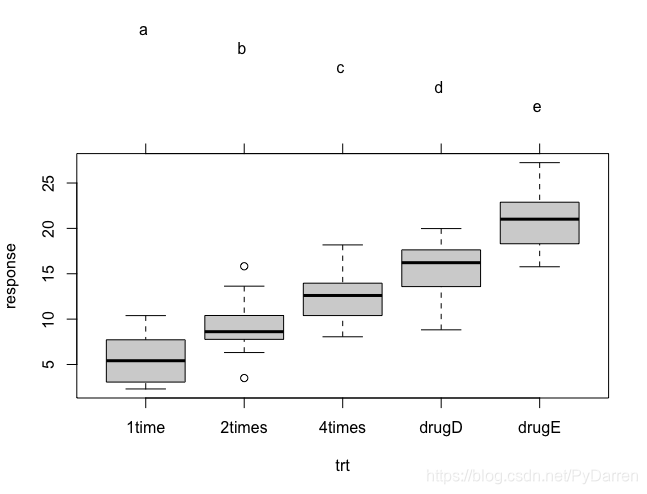
利用multcomp包進行多重檢驗更為全面(並沒感覺很好用)。
library(multcomp)
par(mar=c(5,4,6,2))
tuk <- glht(fit,linfct=mcp(trt="Tukey"))
plot(cld(tuk,level = 0.5),col="lightgrey")
在單因素方差分析中,我們假設資料服從正態分佈,各組方差相等。可以使用Q-Q圖來檢驗正態性假設。
#用Q-Q圖進行正態性假設檢驗 library(car) qqPlot(lm(response ~ trt, data = cholesterol), simulate=TRUE, main="Q-Q Plot", labels=FALSE)
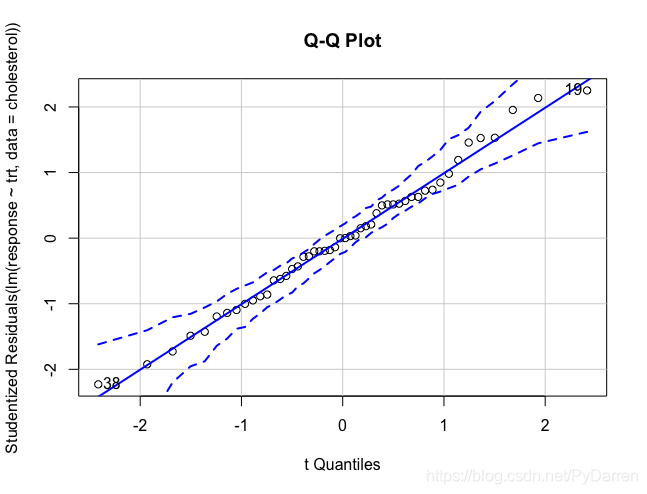
可見資料落在95%置信區間內,滿足正態性假設。
接下來進行各組的方差齊整性檢驗,原假設是方差沒有顯著不同。
#方差齊整性檢驗
bartlett.test(response ~ trt, data = cholesterol)
Bartlett test of homogeneity of variances
data: response by trt
Bartlett's K-squared = 0.57975, df = 4, p-value = 0.9653方差齊整性對離群點很敏感,利用car包的outlierTest()函式可以用來檢測離群點:
> #離群點檢測
> outlierTest(fit)
No Studentized residuals with Bonferonni p < 0.05
Largest |rstudent|:
rstudent unadjusted p-value Bonferonni p
19 2.251149 0.029422 NA
#從輸出結果來看並沒有離群點單因素協方差分析
單因素協方差分析對單因素分析進行了擴充套件,包含一個或多個定量的協變數。
> data(litter,package="multcomp")
> attach(litter)
> table(dose)
dose
0 5 50 500
20 19 18 17
> aggregate(weight,by=list(dose),FUN=mean)
Group.1 x
1 0 32.30850
2 5 29.30842
3 50 29.86611
4 500 29.64647
> fit <- aov(weight ~ gesttime + dose)
> summary(fit)
Df Sum Sq Mean Sq F value Pr(>F)
gesttime 1 134.3 134.30 8.049 0.00597 **
dose 3 137.1 45.71 2.739 0.04988 *
Residuals 69 1151.3 16.69
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1使用effects包的effect()函式獲得調整之後的組均值。
> #獲得去除協變數效應之後的組均值
> library(effects)
> effect("dose",fit)
dose effect
dose
0 5 50 500
32.35367 28.87672 30.56614 29.33460
