關於二叉樹的前序、中序、後序三種遍歷
二叉樹遍歷分為三種:前序、中序、後序,其中序遍歷最為重要。為啥叫這個名字?是根據根節點的順序命名的。
比如上圖正常的一個滿節點,A:根節點、B:左節點、C:右節點,前序順序是ABC(根節點排最先,然後同級先左後右);中序順序是BAC(先左後根最後右);後序順序是BCA(先左後右最後根)。
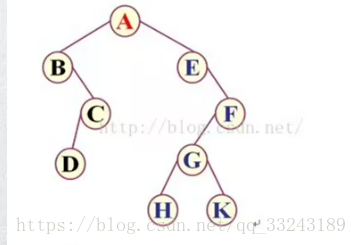
比如上圖二叉樹遍歷結果
前序遍歷:ABCDEFGHK
中序遍歷:BDCAEHGKF
後序遍歷:DCBHKGFEA
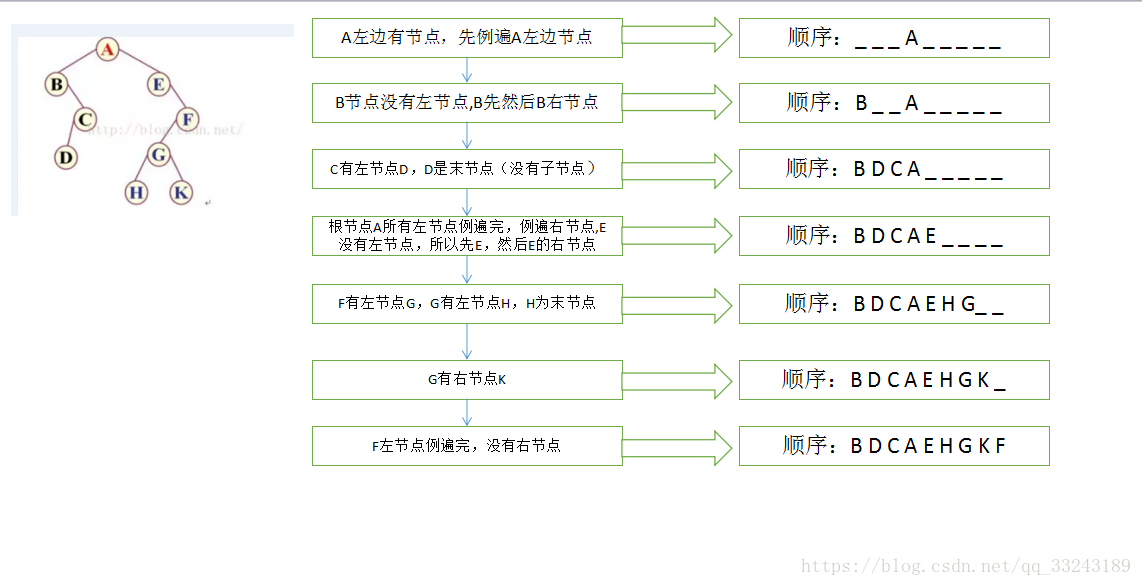
分析中序遍歷如下圖,中序比較重要(java很多樹排序是基於中序,後面講解分析)
相關推薦
第六章樹和二叉樹作業1—二叉樹--計算機17級 7-1 根據後序和中序遍歷輸出先序遍歷 (25 分)
7-1 根據後序和中序遍歷輸出先序遍歷 (25 分) 本題要求根據給定的一棵二叉樹的後序遍歷和中序遍歷結果,輸出該樹的先序遍歷結果。 輸入格式: 第一行給出正整數N(≤30),是樹中結點的個數。隨後兩行,每行給出N個整數,分別對應後序遍歷和中序遍歷結果,數字間以空
資料結構與演算法 -- 二叉樹鏈式詳解((非)/遞迴遍歷,葉子個數,深度計算)
前言 PS:樹型結構是一種重要的非線性資料結構,教科書上一般都是樹與二叉樹,由此可見,樹和二叉樹是有區別和聯絡的,網上有人說二叉樹是樹的一種特殊形式,但經過查資料,樹和二叉樹沒有一個肯定的說法,但唯一可以肯定都是樹型結構。但是按照定義來看二叉樹並不是樹的一種特殊形式(下面解釋)。樹型資料結構的作
C++二叉樹的構建及求深度,葉子數量,層次遍歷
include include include include using namespace std; struct Tree { char info; T
二叉樹前序、中序遍歷得到後序遍歷
() level struct OS spa str sel src [] 二叉樹的前序遍歷為:{1,2,4,7,3,5,6,8},中序遍歷為:{4,7,2,1,5,3,8,6},求後序遍歷 # -*- coding:utf-8 -*- class Nod
數據結構35:二叉樹前序遍歷、中序遍歷和後序遍歷
tdi 代碼 nod 完成 循環 同時 reat pan 設置 遞歸算法底層的實現使用的是棧存儲結構,所以可以直接使用棧寫出相應的非遞歸算法。 先序遍歷的非遞歸算法 從樹的根結點出發,遍歷左孩子的同時,先將每個結點的右孩子壓棧。當遇到結點沒有左孩子的時候,取棧頂的右
二叉樹前序、中序、後序(遞迴 / 非遞迴)遍歷
前語 二叉樹的遍歷是指按一定次序訪問二叉樹中的每一個結點,且每個節點僅被訪問一次。 前序遍歷 若二叉樹非空,則進行以下次序的遍歷: 根節點—>根節點的左子樹—>根節點的右子樹 若要遍歷左子樹和右子樹,仍然需要按照以上次序進行,所以前序遍歷也是一個遞
【演算法】二叉樹前序、中序、後序遍歷相互求法(轉)
二叉樹前序、中序、後序遍歷相互求法 原文地址 今天來總結下二叉樹前序、中序、後序遍歷相互求法,即如果知道兩個的遍歷,如何求第三種遍歷方法,比較笨的方法是畫出來二叉樹,然後根據各種遍歷不同的特性來求,也可以程式設計求出,下面我們分別說明。
已知中序、後序構造二叉樹(關鍵詞:二叉樹/前序/先序/中序/後序/先根/中根/後根/遍歷/搜尋/查詢)
已知中序、後序構造二叉樹 遞迴演算法 def buildTree(inorder, postorder): if inorder and postorder: postRootVal = postorder
已知前序、中序構造二叉樹(關鍵詞:二叉樹/前序/先序/中序/後序/先根/中根/後根/遍歷/搜尋/查詢)
已知前序、中序構造二叉樹 實現 def buildTree(self, preorder, inorder): if inorder: rootVal = preorder.pop(0) rootIdx = inorder.index(rootVal) root
二叉樹——前、中、後序遍歷遞迴以及非遞迴寫法
#include <iostream> #include <stack> #include <queue> using namespace std; typedef struct Node{ int data; Node *l
關於二叉樹的前序、中序、後序三種遍歷
二叉樹遍歷分為三種:前序、中序、後序,其中序遍歷最為重要。為啥叫這個名字?是根據根節點的順序命名的。比如上圖正常的一個滿節點,A:根節點、B:左節點、C:右節點,前序順序是ABC(根節點排最先,然後同級先左後右);中序順序是BAC(先左後根最後右);後序順序是BCA(先左後右
二叉樹前序、中序、後序遍歷求法
二叉樹前序、中序、後序遍歷相互求法 二叉樹的三種遍歷方法: 前序遍歷: 1.訪問根節點 2.前序遍歷左子樹 3.前序遍歷右子樹 中序遍歷: 1.中序遍歷左子樹 2.訪問根節點 3.中序遍歷右子樹 後序遍歷: 1.後序遍歷左子樹 2.後序遍歷右子樹 3.訪問根節
二叉樹前序、中序、後序遞迴與非遞迴遍歷+層序遍歷(java)
前序遞迴遍歷演算法:訪問根結點-->遞迴遍歷根結點的左子樹-->遞迴遍歷根結點的右子樹 中序遞迴遍歷演算法:遞迴遍歷根結點的左子樹-->訪問根結點-->遞迴遍歷根結點的右子樹 後序遞迴遍歷演算法:遞迴遍歷根結
已知二叉樹前序、中序遍歷用python求後序遍歷
這裡用到遞迴的方法:遞迴的關鍵是找到出口和遞迴的狀態(也就是要寫出遞迴第一個完整的過程),這樣計算機才能明白以後的若干步怎麼去走。當然,實際中遞迴的方法效率不高(不表明它不快),因為要頻繁呼叫函式本身,所以容易爆炸(哈哈哈)。程式碼:def last_sort(str1, s
由二叉樹前序序列、中序序列輸出相應後續序列
題目描述: 給定一棵二叉樹的前序遍歷和中序遍歷序列,求其後序遍歷續列(注:給定中序遍歷序列,只要知道前序、後序或者層次遍歷中的一種就能唯一的確定一棵二叉樹)。 輸入: 兩個字串,其長度均小於26。 第
二叉樹前序、中序、後序遍歷非遞迴寫法的透徹解析
圖a的程式碼段(ii)也可寫成圖b的理由是:由於是葉子節點,p=-=p->rchild;之後p肯定為空。為空,還需經過新一輪的程式碼段(i)嗎?顯然不需。(因為不滿足迴圈條件)那就直接進入程式碼段(ii)。看!最後還是一樣的吧。還是連續出棧兩次。看到這裡,要仔細想想哦!相信你一定會明白的。
經典演算法之非遞迴演算法實現二叉樹前、中、後序遍歷
/************************ author's email:[email protected] date:2017.12.24 非遞迴演算法實現二叉樹前、中、後序遍歷 ************************/ #include<
二叉樹前序、中序、後序遍歷相互求法
0.二叉樹相關的基本概念和性質: 定義: 1、滿二叉樹:一棵深度為k且有2的k次方減1個結點的二叉樹稱為滿二叉樹 2、完全二叉樹:如果有深度為k的,有n個結點的二叉樹,當且僅當其每一個結點都與深度為k的滿二叉樹中編號從1至n的結點一一對應時,稱之為完全二叉樹。 性質: 1、二叉樹的第i層上至多有2的i-
資料結構(六)——二叉樹 前序、中序、後序、層次遍歷及非遞迴實現 查詢、統計個數、比較、求深度的遞迴實現
一、基本概念每個結點最多有兩棵子樹,左子樹和右子樹,次序不可以顛倒。性質:1、非空二叉樹的第n層上至多有2^(n-1)個元素。2、深度為h的二叉樹至多有2^h-1個結點。滿二叉樹:所有終端都在同一層次,
二叉樹前序遍歷、中序遍歷、後序遍歷、層序遍歷的直觀理解
0. 寫在最前面 複習到二叉樹,看到網上諸多部落格文章各種繞,記得頭暈。個人覺得數學、演算法這些東西都是可以更直觀簡潔地表示,然後被記住的,並不需要靠死記硬背。 本文的程式基本來源於《大話資料結構》,個人感覺是一本非常好的書,推薦去看。 1. 為什麼叫前序、