資料結構——二叉樹的遍歷
“樹”是一種重要的資料結構,本文淺談二叉樹的遍歷問題,採用C語言描述。
一、二叉樹基礎
1)定義:有且僅有一個根結點,除根節點外,每個結點只有一個父結點,最多含有兩個子節點,子節點有左右之分。
2)儲存結構
二叉樹的儲存結構可以採用順序儲存,也可以採用鏈式儲存,其中鏈式儲存更加靈活。
在鏈式儲存結構中,與線性連結串列類似,二叉樹的每個結點採用結構體表示,結構體包含三個域:資料域、左指標、右指標。
二叉樹在C語言中的定義如下:
struct BiTreeNode{ int c; struct BiTreeNode *left; struct BiTreeNode *right; };
二、二叉樹的遍歷
“遍歷”是二叉樹各種操作的基礎。二叉樹是一種非線性結構,其遍歷不像線性連結串列那樣容易,無法通過簡單的迴圈實現。
二叉樹是一種樹形結構,遍歷就是要讓樹中的所有節點被且僅被訪問一次,即按一定規律排列成一個線性佇列。二叉(子)樹是一種遞迴定義的結構,包含三個部分:根結點(N)、左子樹(L)、右子樹(R)。根據這三個部分的訪問次序對二叉樹的遍歷進行分類,總共有6種遍歷方案:NLR、LNR、LRN、NRL、RNL和LNR。研究二叉樹的遍歷就是研究這6種具體的遍歷方案,顯然根據簡單的對稱性,左子樹和右子樹的遍歷可互換,即NLR與NRL、LNR與RNL、LRN與RLN,分別相類似,因而只需研究NLR、LNR和LRN三種即可,分別稱為“先序遍歷”、“中序遍歷”和“後序遍歷”。
二叉樹遍歷通常借用“棧”這種資料結構實現,有兩種方式:遞迴方式及非遞迴方式。
在遞迴方式中,棧是由作業系統維護的,使用者不必關心棧的細節操作,使用者只需關心“訪問順序”即可。因而,採用遞迴方式實現二叉樹的遍歷比較容易理解,演算法簡單,容易實現。
遞迴方式實現二叉樹遍歷的C語言程式碼如下:
//先序遍歷--遞迴 int traverseBiTreePreOrder(BiTreeNode *ptree,int (*visit)(int)) { if(ptree) { if(visit(ptree->c)) if(traverseBiTreePreOrder(ptree->left,visit)) if(traverseBiTreePreOrder(ptree->right,visit)) return 1; //正常返回 return 0; //錯誤返回 }else return 1; //正常返回 } //中序遍歷--遞迴 int traverseBiTreeInOrder(BiTreeNode *ptree,int (*visit)(int)) { if(ptree) { if(traverseBiTreeInOrder(ptree->left,visit)) if(visit(ptree->c)) if(traverseBiTreeInOrder(ptree->right,visit)) return 1; return 0; }else return 1; } //後序遍歷--遞迴 int traverseBiTreePostOrder(BiTreeNode *ptree,int (*visit)(int)) { if(ptree) { if(traverseBiTreePostOrder(ptree->left,visit)) if(traverseBiTreePostOrder(ptree->right,visit)) if(visit(ptree->c)) return 1; return 0; }else return 1; }
以上程式碼中,visit為一函式指標,用於傳遞二叉樹中對結點的操作方式,其原型為:int (*visit)(char)。
大家知道,函式在呼叫時,會自動進行棧的push,呼叫返回時,則會自動進行棧的pop。函式遞迴呼叫無非是對一個棧進行返回的push與pop,既然遞迴方式可以實現二叉樹的遍歷,那麼借用“棧”採用非遞迴方式,也能實現遍歷。但是,這時的棧操作(push、pop等)是由使用者進行的,因而實現起來會複雜一些,而且也不容易理解,但有助於我們對樹結構的遍歷有一個深刻、清晰的理解。
在討論非遞迴遍歷之前,我們先定義棧及各種需要用到的棧操作:
//棧的定義,棧的資料是“樹結點的指標”
struct Stack{
BiTreeNode **top;
BiTreeNode **base;
int size;
};
#define STACK_INIT_SIZE 100
#define STACK_INC_SIZE 10
//初始化空棧,預分配儲存空間
Stack* initStack()
{
Stack *qs=NULL;
qs=(Stack *)malloc(sizeof(Stack));
qs->base=(BiTreeNode **)calloc(STACK_INIT_SIZE,sizeof(BiTreeNode *));
qs->top=qs->base;
qs->size=STACK_INIT_SIZE;
return qs;
}
//取棧頂資料
BiTreeNode* getTop(Stack *qs)
{
BiTreeNode *ptree=NULL;
if(qs->top==qs->base)
return NULL;
ptree=*(qs->top-1);
return ptree;
}
//入棧操作
int push(Stack *qs,BiTreeNode *ptree)
{
if(qs->top-qs->base>=qs->size)
{
qs->base=(BiTreeNode **)realloc(qs->base,(qs->size+STACK_INC_SIZE)*sizeof(BiTreeNode *));
qs->top=qs->base+qs->size;
qs->size+=STACK_INC_SIZE;
}
*qs->top++=ptree;
return 1;
}
//出棧操作
BiTreeNode* pop(Stack *qs)
{
if(qs->top==qs->base)
return NULL;
return *--qs->top;
}
//判斷棧是否為空
int isEmpty(Stack *qs)
{
return qs->top==qs->base;
}首先考慮非遞迴先序遍歷(NLR)。在遍歷某一個二叉(子)樹時,以一當前指標記錄當前要處理的二叉(左子)樹,以一個棧儲存當前樹之後處理的右子樹。首先訪問當前樹的根結點資料,接下來應該依次遍歷其左子樹和右子樹,然而程式的控制流只能處理其一,所以考慮將右子樹的根儲存在棧裡面,當前指標則指向需先處理的左子樹,為下次迴圈做準備;若當前指標指向的樹為空,說明當前樹為空樹,不需要做任何處理,直接彈出棧頂的子樹,為下次迴圈做準備。相應的C語言程式碼如下:
//先序遍歷--非遞迴
int traverseBiTreePreOrder2(BiTreeNode *ptree,int (*visit)(int))
{
Stack *qs=NULL;
BiTreeNode *pt=NULL;
qs=initStack();
pt=ptree;
while(pt || !isEmpty(qs))
{
if(pt)
{
if(!visit(pt->c)) return 0; //錯誤返回
push(qs,pt->right);
pt=pt->left;
}
else pt=pop(qs);
}
return 1; //正常返回
}相對於非遞迴先序遍歷,非遞迴的中序/後序遍歷稍複雜一點。
對於非遞迴中序遍歷,若當前樹不為空樹,則訪問其根結點之前應先訪問其左子樹,因而先將當前根節點入棧,然後考慮其左子樹,不斷將非空的根節點入棧,直到左子樹為一空樹;當左子樹為空時,不需要做任何處理,彈出並訪問棧頂結點,然後指向其右子樹,為下次迴圈做準備。
//中序遍歷--非遞迴
int traverseBiTreeInOrder2(BiTreeNode *ptree,int (*visit)(int))
{
Stack *qs=NULL;
BiTreeNode *pt=NULL;
qs=initStack();
pt=ptree;
while(pt || !isEmpty(qs))
{
if(pt)
{
push(qs,pt);
pt=pt->left;
}
else
{
pt=pop(qs);
if(!visit(pt->c)) return 0;
pt=pt->right;
}
}
return 1;
}
//中序遍歷--非遞迴--另一種實現方式
int traverseBiTreeInOrder3(BiTreeNode *ptree,int (*visit)(int))
{
Stack *qs=NULL;
BiTreeNode *pt=NULL;
qs=initStack();
push(qs,ptree);
while(!isEmpty(qs))
{
while(pt=getTop(qs)) push(qs,pt->left);
pt=pop(qs);
if(!isEmpty(qs))
{
pt=pop(qs);
if(!visit(pt->c)) return 0;
push(qs,pt->right);
}
}
return 1;
}最後談談非遞迴後序遍歷。由於在訪問當前樹的根結點時,應先訪問其左、右子樹,因而先將根結點入棧,接著將右子樹也入棧,然後考慮左子樹,重複這一過程直到某一左子樹為空;如果當前考慮的子樹為空,若棧頂不為空,說明第二棧頂對應的樹的右子樹未處理,則彈出棧頂,下次迴圈處理,並將一空指標入棧以表示其另一子樹已做處理;若棧頂也為空樹,說明第二棧頂對應的樹的左右子樹或者為空,或者均已做處理,直接訪問第二棧頂的結點,訪問完結點後,若棧仍為非空,說明整棵樹尚未遍歷完,則彈出棧頂,併入棧一空指標表示第二棧頂的子樹之一已被處理。
//後序遍歷--非遞迴
int traverseBiTreePostOrder2(BiTreeNode *ptree,int (*visit)(int))
{
Stack *qs=NULL;
BiTreeNode *pt=NULL;
qs=initStack();
pt=ptree;
while(1) //迴圈條件恆“真”
{
if(pt)
{
push(qs,pt);
push(qs,pt->right);
pt=pt->left;
}
else if(!pt)
{
pt=pop(qs);
if(!pt)
{
pt=pop(qs);
if(!visit(pt->c)) return 0;
if(isEmpty(qs)) return 1;
pt=pop(qs);
}
push(qs,NULL);
}
}
return 1;
}
三、二叉樹的建立
談完二叉樹的遍歷之後,再來談談二叉樹的建立,這裡所說的建立是指從控制檯依次(先/中/後序)輸入二叉樹的各個結點元素(此處為字元),用“空格”表示空樹。
由於控制檯輸入是儲存在輸入緩衝區內,因此遍歷的“順序”就反映在讀取輸入字元的次序上。
以下是遞迴方式實現的先序建立二叉樹的C程式碼。
//建立二叉樹--先序輸入--遞迴
BiTreeNode* createBiTreePreOrder()
{
BiTreeNode *ptree=NULL;
char ch;
ch=getchar();
if(ch==' ')
ptree=NULL;
else
{
ptree=(struct BiTreeNode *)malloc(sizeof(BiTreeNode));
ptree->c=ch;
ptree->left=createBiTreePreOrder();
ptree->right=createBiTreePreOrder();
}
return ptree;
}對於空樹,函式直接返回即可;對於非空樹,先讀取字元並賦值給當前根結點,然後建立左子樹,最後建立右子樹。因此,要先知道當前要建立的樹是否為空,才能做相應處理,“先序”遍歷方式很好地符合了這一點。但是中序或後序就不一樣了,更重要的是,中序或後序方式輸入的字元序列無法唯一確定一個二叉樹。我還沒有找到中序/後序實現二叉樹的建立(控制檯輸入)的類似簡單的方法,希望各位同仁網友不吝賜教哈!
四、執行及結果
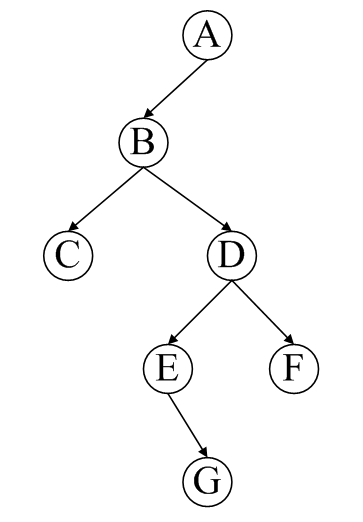
採用如下的二叉樹進行測試,首先先序輸入建立二叉樹,然後依次呼叫各個遍歷函式。
先序輸入的格式:ABC ^ ^ D E ^ G ^ ^ F ^ ^ ^ (其中, ^ 表示空格字元)
遍歷操作採用標準I/O庫中的putchar函式,其原型為:int putchar(int);
各種形式遍歷輸出的結果為:
先序:ABCDEGF
中序:CBEGDFA
後序:CGEFDBA
測試程式的主函式如下:
int main(int argc, char* argv[])
{
BiTreeNode *proot=NULL;
printf("InOrder input chars to create a BiTree: ");
proot=createBiTreePreOrder(); //輸入(ABC DE G F )
printf("PreOrder Output the BiTree recursively: ");
traverseBiTreePreOrder(proot,putchar);
printf("\n");
printf("PreOrder Output the BiTree non-recursively: ");
traverseBiTreePreOrder2(proot,putchar);
printf("\n");
printf("InOrder Output the BiTree recursively: ");
traverseBiTreeInOrder(proot,putchar);
printf("\n");
printf("InOrder Output the BiTree non-recursively(1): ");
traverseBiTreeInOrder2(proot,putchar);
printf("\n");
printf("InOrder Output the BiTree non-recursively(2): ");
traverseBiTreeInOrder3(proot,putchar);
printf("\n");
printf("PostOrder Output the BiTree non-recursively: ");
traverseBiTreePostOrder(proot,putchar);
printf("\n");
printf("PostOrder Output the BiTree recursively: ");
traverseBiTreePostOrder2(proot,putchar);
printf("\n");
return 0;
}