B樹(也叫B-樹)、B+樹、B*樹
0. 簡介
在此宣告,B-Tree最正確的翻譯應該為B樹,而不是B-樹,也即並沒有B-樹的說法,二叉樹叫Binary Tree,二叉搜尋樹叫Binary Search Tree(BST)B樹叫Balance Tree,簡寫為B-Tree (注意是這兩個單詞連起來的意思,不是減號),B+樹是B+ Tree。
1. BST(Binary Search Tree,即二叉搜尋樹,並不是B樹)
- 所有非葉子結點至多擁有兩個兒子(Left和Right,可以只有一個);
- 所有結點儲存一個關鍵字;
- 非葉子結點的左指標指向小於其關鍵字的子樹,右指標指向大於其關鍵字的子樹;
如:
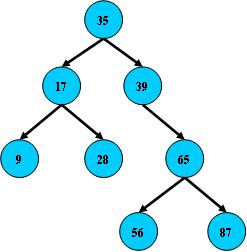
B樹的搜尋,從根結點開始,如果查詢的關鍵字與結點的關鍵字相等,那麼就命中;否則,如果查詢關鍵字比結點關鍵字小,就進入左兒子;如果比結點關鍵字大,就進入右兒子;如果左兒子或右兒子的指標為空,則報告找不到相應的關鍵字;
如果BST樹的所有非葉子結點的左右子樹的結點數目均保持差不多(平衡),那麼B樹的搜尋效能逼近二分查詢;但它比連續記憶體空間的二分查詢的優點是,改變B樹結構(插入與刪除結點)不需要移動大段的記憶體資料,甚至通常是常數開銷;
如:
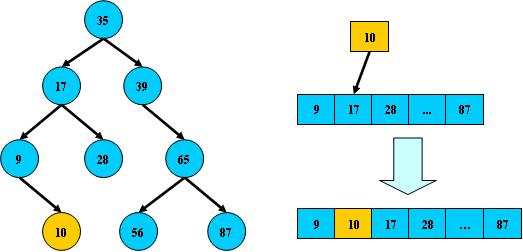
右邊也是一個BST樹,但它的搜尋效能已經是線性的了;同樣的關鍵字集合有可能導致不同的樹結構索引;所以,使用BST樹還要考慮儘可能讓B樹保持左圖的結構,和避免右圖的結構,也就是所謂的“平衡”問題;
實際使用的BST樹都是在原BST樹的基礎上加上平衡演算法,即“平衡二叉樹”;如何保持BST樹結點分佈均勻的平衡演算法是平衡二叉樹的關鍵;平衡演算法是一種在BST樹中插入和刪除結點的策略;
2. B樹也翻譯為B-樹(是一種多路搜尋樹 並不是二叉的)
- 定義任意非葉子結點最多隻有M個兒子;且M>2;
- 根結點的兒子數為[2, M];
- 除根結點以外的非葉子結點的兒子數為[M/2, M];
- 每個結點存放至少M/2-1(取上整)和至多M-1個關鍵字;(至少2個關鍵字)
- 非葉子結點的關鍵字個數=指向兒子的指標個數-1;
- 非葉子結點的關鍵字:K[1], K[2], …, K[M-1];且K[i] < K[i+1];
- 非葉子結點的指標:P[1], P[2], …, P[M];其中P[1]指向關鍵字小於K[1]的子樹,P[M]指向關鍵字大於K[M-1]的子樹,其它P[i]指向關鍵字屬於(K[i-1], K[i])的子樹;
- 所有葉子結點位於同一層;
如:(M=3)
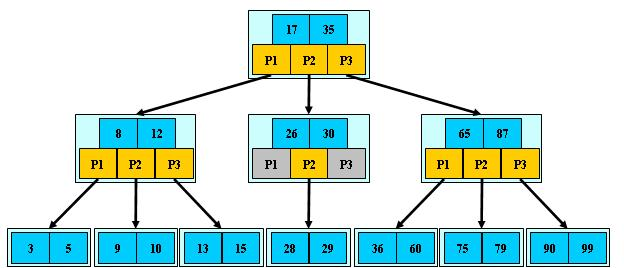
B-樹的搜尋,從根結點開始,對結點內的關鍵字(有序)序列進行二分查詢,如果命中則結束,否則進入查詢關鍵字所屬範圍的兒子結點;重複,直到所對應的兒子指標為空,或已經是葉子結點;
B-樹的特性:
- 關鍵字集合分佈在整顆樹中;
- 任何一個關鍵字出現且只出現在一個結點中;
- 搜尋有可能在非葉子結點結束;
- 其搜尋效能等價於在關鍵字全集內做一次二分查詢;
- 自動層次控制;
由於限制了除根結點以外的非葉子結點,至少含有M/2個兒子,確保了結點的至少利用率,其最底搜尋效能為O(log2N),M為設定的非葉子結點最多子樹個數,N為關鍵字總數;所以B-樹的效能總是等價於二分查詢(與M值無關),也就沒有B樹平衡的問題;
3. B+樹(B+樹是B-樹的變體,也是一種多路搜尋樹)
- 其定義基本與B-樹同,除了:
- 非葉子結點的子樹指標與關鍵字個數相同;
- 非葉子結點的子樹指標P[i],指向關鍵字值屬於[K[i], K[i+1])的子樹
(B-樹是開區間); - 為所有葉子結點增加一個鏈指標;
- 所有關鍵字都在葉子結點出現;
如:(M=3)
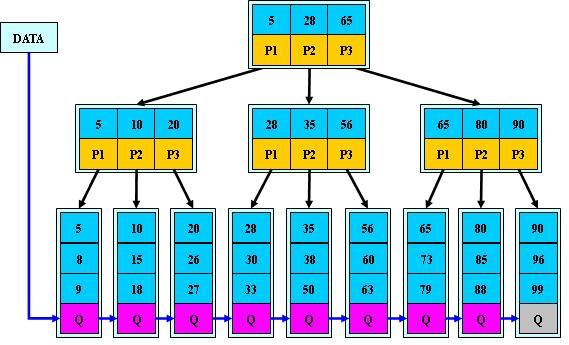
B+的搜尋與B-樹也基本相同,區別是B+樹只有達到葉子結點才命中(B-樹可以在非葉子結點命中),其效能也等價於在關鍵字全集做一次二分查詢;
B+的特性:
1.所有關鍵字都出現在葉子結點的連結串列中(稠密索引),且連結串列中的關鍵字恰好是有序的;
2.不可能在非葉子結點命中;
3.非葉子結點相當於是葉子結點的索引(稀疏索引),葉子結點相當於是儲存(關鍵字)資料的資料層;
4.更適合檔案索引系統;
4. B*樹(B+樹的變體,在B+樹的非根和非葉子結點再增加指向兄弟的指標)
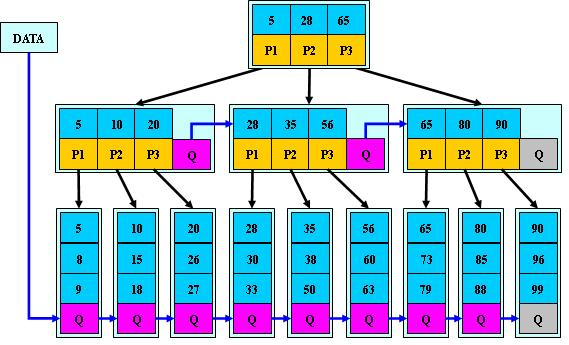
B樹定義了非葉子結點關鍵字個數至少為(2/3) * M,即塊的最低使用率為2/3(代替B+樹的1/2);
B+樹的分裂:當一個結點滿時,分配一個新的結點,並將原結點中1/2的資料複製到新結點,最後在父結點中增加新結點的指標;B+樹的分裂隻影響原結點和父結點,而不會影響兄弟結點,所以它不需要指向兄弟的指標;
B樹的分裂:當一個結點滿時,如果它的下一個兄弟結點未滿,那麼將一部分資料移到兄弟結點中,再在原結點插入關鍵字,最後修改父結點中兄弟結點的關鍵字(因為兄弟結點的關鍵字範圍改變了);如果兄弟也滿了,則在原結點與兄弟結點之間增加新結點,並各複製1/3的資料到新結點,最後在父結點增加新結點的指標;
所以,B*樹分配新結點的概率比B+樹要低,空間使用率更高;
5. 小結
- BST樹:二叉樹,每個結點只儲存一個關鍵字,等於則命中,小於走左結點,大於走右結點;
- B樹(錯誤叫法是B-樹):多路搜尋樹,每個結點儲存M/2到M個關鍵字,非葉子結點儲存指向關鍵字範圍的子結點;所有關鍵字在整顆樹中出現,且只出現一次,非葉子結點可以命中;
- B+樹:在B-樹基礎上,為葉子結點增加連結串列指標,所有關鍵字都在葉子結點中出現,非葉子結點作為葉子結點的索引;B+樹總是到葉子結點才命中;
- B*樹:在B+樹基礎上,為非葉子結點也增加連結串列指標,將結點的最低利用率從1/2提高到2/3;
