實現了樹的兄弟孩子表示法，插入新資料，查詢某個資料，前序遍歷，中序遍歷，後序遍歷。

相關概念：
每一棵樹都有一個根節點。
每個節點可以有多個兒子節點，沒有兒子的結點叫做葉子節點。
具有相同父親的節點叫做兄弟節點。
對於任意一個節點ni，ni的深度為從根到ni的唯一路徑的長。因此，根的深度是0。
ni的高是從ni到一片樹葉的最長路徑的長。因此葉子節點的高是0。一棵樹的高等於它的根的高。
一棵樹的深度等於它的最深的樹葉的深度，該深度等於這棵樹的高。

樹的實現：
使用樹的兄弟孩子表示法。
typedef struct STreeNode* pSTreeNode;

struct STreeNode
{
int nValue;
pSTreeNode pFirstChild;
pSTreeNode pNextBrother;

STreeNode()
{
    nValue = 0;
    pFirstChild = NULL;
    pNextBrother = NULL;
}

};

其中pFirstChild(左孩子節點)表示第一個兒子節點，pNextBrother(右孩子節點)表示下一個兄弟節點。

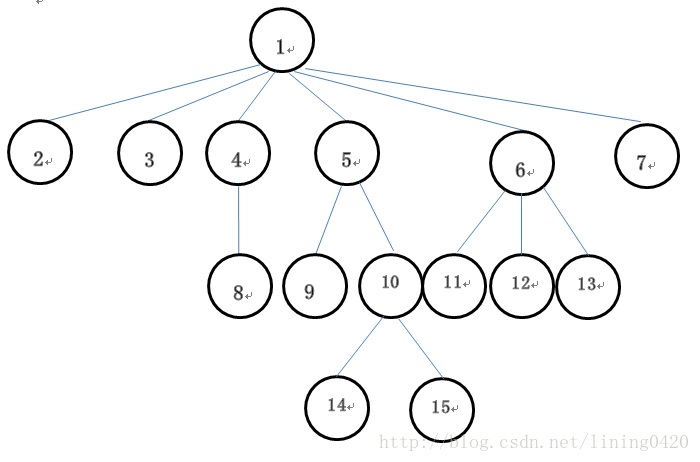
一顆普通樹表示如下：

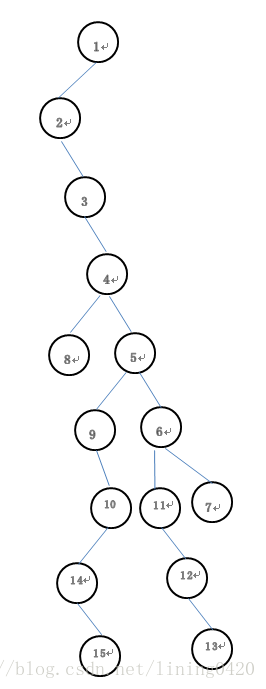
使用兄弟孩子表示法表示如下：

樹的遍歷：
前序遍歷（先根節點，後左孩子節點，再右孩子結點）
中序遍歷（先左孩子結點，後根節點，再右孩子結點）
後序遍歷（先做孩子節點，後右孩子結點，再根節點）

程式碼如下：

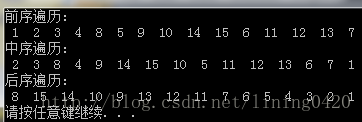
#include <iostream>
 

using namespace std;

typedef struct STreeNode* pSTreeNode;
typedef int TreeDataType;

struct STreeNode
{
    TreeDataType data;
    pSTreeNode pFirstChild;
    pSTreeNode pNextBrother;

    STreeNode( TreeDataType Value )
    {
        data = Value;
        pFirstChild = NULL;
        pNextBrother = NULL
 
;
    }
}; 


class CTree
{
public:
    CTree();
    CTree( TreeDataType Value );
    ~CTree();


public:
    void Insert( TreeDataType parentValue, TreeDataType Value );    //  parentValue：該節點的父結點；Value：該節點的值
    void InsertBrother( pSTreeNode pParentNode, TreeDataType Value );

    pSTreeNode Search( pSTreeNode pNode, TreeDataType Value );

    void Preorder( pSTreeNode pNode );      //  前序遍歷
    void Inorder( pSTreeNode pNode );       //  中序遍歷
    void postorder( pSTreeNode pNode );     //  後續遍歷

    void PrintNode( pSTreeNode pNode );
    void FreeMemory( pSTreeNode pNode );    //  釋放記憶體

    public:
    pSTreeNode pRoot;
};

CTree::CTree()
{
    pRoot = NULL;
}

CTree::CTree( TreeDataType Value )
{
    pRoot = new STreeNode( Value );
    if ( pRoot == NULL )
        return;
}

CTree::~CTree()
{
    if (pRoot == NULL )
        return;

    FreeMemory( pRoot );
}

void CTree::FreeMemory( pSTreeNode pNode )
{
    if ( pNode == NULL )
        return;

    if ( pNode->pFirstChild != NULL )
        FreeMemory( pNode->pFirstChild );

    if ( pNode->pNextBrother != NULL )
        FreeMemory( pNode->pNextBrother );

    delete pNode;
    pNode = NULL;
}

void CTree::Insert( TreeDataType parentValue, TreeDataType Value )
{
    if ( pRoot == NULL )
        return;

    pSTreeNode pFindNode = Search( pRoot, parentValue );
    if ( pFindNode == NULL )
        return;

    if ( pFindNode->pFirstChild == NULL )
    {
        pFindNode->pFirstChild = new STreeNode( Value );
        return;
    }
    else
    {
        InsertBrother( pFindNode->pFirstChild, Value );
        return;
    }
}

void CTree::InsertBrother( pSTreeNode pBrotherNode, TreeDataType Value )
{
    if ( pBrotherNode->pNextBrother != NULL )
        InsertBrother( pBrotherNode->pNextBrother, Value );
    else
    {
        pBrotherNode->pNextBrother = new STreeNode( Value );
        return;
    }

}

pSTreeNode CTree::Search( pSTreeNode pNode, TreeDataType Value )
{
    if ( pNode == NULL )
        return NULL;

    if ( pNode->data == Value )
        return pNode;

    if ( pNode->pFirstChild == NULL && pNode->pNextBrother == NULL )
        return NULL;
    else
    {
        if ( pNode->pFirstChild != NULL )
        {
            pSTreeNode pNodeTemp = Search( pNode->pFirstChild, Value );
            if ( pNodeTemp != NULL )
                return pNodeTemp;
            else
            {
                return Search( pNode->pNextBrother, Value );
            }
        }
        else
            return Search( pNode->pNextBrother, Value );
    }
}

void CTree::Preorder( pSTreeNode pNode )
{
    if (pNode == NULL)
        return;
    cout << " " << pNode->data << " ";

    Preorder( pNode->pFirstChild );
    Preorder( pNode->pNextBrother );
}

void CTree::Inorder( pSTreeNode pNode )
{
    if ( pNode == NULL )
        return;

    Inorder( pNode->pFirstChild );
    cout << " " << pNode->data << " ";
    Inorder( pNode->pNextBrother );
}

void CTree::postorder( pSTreeNode pNode )
{
    if ( pNode == NULL )
        return;

    postorder( pNode->pFirstChild );
    postorder( pNode->pNextBrother );
    cout << " " << pNode->data << " ";
}

int main()
{
    CTree* pTree = new CTree( 1 );
    if ( pTree == NULL )
        return 0;

    pTree->Insert( 1, 2 );
    pTree->Insert( 1, 3 );
    pTree->Insert( 1, 4 );
    pTree->Insert( 1, 5 );
    pTree->Insert( 1, 6 );
    pTree->Insert( 1, 7 );
    pTree->Insert( 4, 8 );
    pTree->Insert( 5, 9 );
    pTree->Insert( 5, 10 );
    pTree->Insert( 6, 11 );
    pTree->Insert( 6, 12 );
    pTree->Insert( 6, 13 );
    pTree->Insert( 10, 14 );
    pTree->Insert( 10, 15 );

    cout << "前序遍歷：" << endl;
    pTree->Preorder( pTree->pRoot );
    cout << endl;

    cout << "中序遍歷：" << endl;
    pTree->Inorder( pTree->pRoot );
    cout << endl;

    cout << "後序遍歷：" << endl;
    pTree->postorder( pTree->pRoot );
    cout << endl;

    delete pTree;
    pTree = NULL;
    system("pause");
    return 1;
}

執行結果如下：