2. 程式人生 > >資料結構（樹，二叉搜尋樹，平衡二叉樹 C++實現）

資料結構（樹，二叉搜尋樹，平衡二叉樹 C++實現）

阿新 • • 發佈：2019-01-27

樹

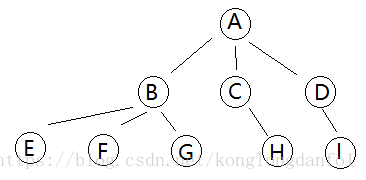
樹（Tree）是n（n>=0）個結點的有限集合。n = 0時稱為空樹。在任意一顆非空樹中：(1)有且僅有一個特定的稱為根（Root）的結點；（2）當n > 1時，其餘結點可分為m （m > 0）個互不相交的有限集 T1 、 T2 、 …… 、 Tm ，其中每一個集合本身又是一個樹，並且稱為根的子樹（SubTree），如下圖所示：

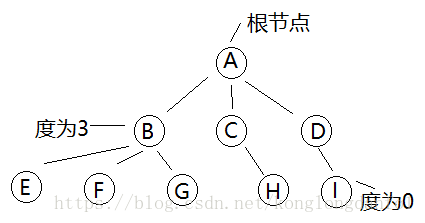
這裡寫圖片描述

樹的結點包含一個數據元素及若干指向其子樹的分支。結點擁有的子樹數稱為結點的度(Degree)。度為0的結點稱為葉結點(Leaf)或終端結點；度不為0的結點稱為非終端結點或分支結點。除根結點之外，分支結點也稱為內部結點。樹的度是樹內各結點的度的最大值。

結點的子樹的根稱為該結點的孩子(Child),相應地，該結點稱為還的雙親（Parent）。同一個雙親的孩子之間互稱兄弟（Sibling）。結點的祖先是從根到結點所經分支上的所有結點。對於 F 來說 B 、 A 都是它的祖先。以某結點為根的子樹中的任一結點都稱為該結點的子孫。B 的子樹有 E 、 F 、 G。如下圖：

這裡寫圖片描述

樹的儲存結構

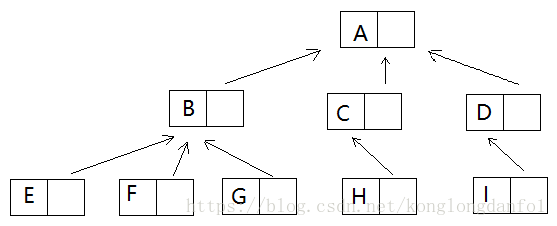
樹的儲存結構有多種，常用的有雙親表示法、孩子表示法、孩子兄弟表示法。

雙親表示法

結構如下：

data parent

其中data是資料域，儲存結點的資料資訊。而parent是指標域，指向該結點的雙親。


template
 
 < typename T>
struct TreeNode
{
  T data;
  TreeNode * parent;
}

之前的樹的儲存結構如下：

這裡寫圖片描述

孩子表示法
data child1 child2 child3 … childd 
template <typename T>
struct TreeNode
{
  T data;
  TreeNode * nodeList;
}

這裡寫圖片描述

孩子兄弟表示法
data firstchild rightsib 
template <typename
 
 T>
struct TreeNode
{
  T data;
  TreeNode * firstchild, * rightsib;
}

這裡寫圖片描述

二叉樹

二叉樹（Binary Tree）是 n （ n >= 0）個結點的有限集合，該集合或者為空集（稱為空二叉樹），或者由一個根結點和兩顆互不相交的、分別稱為根結點的左子樹和右子樹的二叉樹組成。如下圖：

這裡寫圖片描述

二叉樹結點結構一般如下：


struct TreeNode
{
  T data;
  TreeNode * lchild, * rchild;
}
二叉樹遍歷

二叉樹遍歷常用的有4中，分別為前序遍歷、中序遍歷、後序遍歷。其中的前、中、後是按照根結點的遍歷順序來區分的。

前序遍歷

若二叉樹為空，則返回，否則先訪問根結點，然後前序遍歷左子樹，再前序遍歷右子樹。上圖二叉樹的前序遍歷順序為：ABFHKECFIGJ。前序遍歷的程式碼如下：


void preOrderTraverse(TreeNode * node)
{
  if (nullptr == node)
   return;
  std::cout << node->data << std::endl;
  preOrderTraverse(node->lchild);
  preOrderTraverse(node->rchild);
}
中序遍歷

若二叉樹為空，則返回，否則先中序遍歷根結點的左子樹，然後訪問根結點，最後中序遍歷右子樹。上圖二叉樹的中序遍歷順序為：HKDBEAIFCGJ。中序遍歷的程式碼如下：


void inOrderTraverse(TreeNode * node)
{
  if (nullptr == node)
   return;
  inOrderTraverse(node->lchild);
  std::cout << node->data << std::endl;
  inOrderTraverse(node->rchild);
}
後序遍歷

若二叉樹為空，則返回，否則先後序遍歷根結點的左子樹，然後後序遍歷右子樹，最後訪問根結點。上圖二叉樹的後序遍歷順序為：KHDEBIFJGCA。後序遍歷的程式碼如下：


void postOrderTraverse(TreeNode * node)
{
  if (nullptr == node)
   return;
  postOrderTraverse(node->lchild);
  postOrderTraverse(node->rchild);
  std::cout << node->data << std::endl;
}

二叉查詢樹

二叉查詢樹（Binary Sort Tree），又稱為二叉排序樹。它或者是一個樹，或者是就有下列性質的二叉樹。

若它的左子樹不空，則左子樹上所有結點的值均小於它的跟結構的值；

若它的右子樹不空，則右子樹上所有結點的值均大於它的根結點的值；

它的左、右子樹也分別為二叉排序樹。

構造一顆二叉查詢樹的目的，不是為了排序，目的是為了提高查詢和出啊如刪除關鍵字的速度。

二叉查詢樹查詢

二叉樹的查詢沒什麼難度，利用要查詢的值，經過比較和遞迴之類的不難實現：


template<typename T>
void searchElement(TreeNode<T> * node, T key)
{
    if (nullptr == node)
        return nullptr;
    if (key == node->data)
        return node;
    else if (key < node->data)
        searchElement(node->lchild, key);
    else
        searchElement(node->rchild, key);
}
二叉查詢樹插入

插入操作和查詢差不多，如下：


template<typename T>
bool insertElement(TreeNode<T> *& node,T key)
{
    if (nullptr == node)// 空樹
    {
        node = new TreeNode<T>;
        node->data = key;
    }
    else if (key == node->data)// 已經有該關鍵字
    {
        return false;
    }
    else
    {
        if (key < node->data)
        {
            insertElement(node->lchild, key);
        }
        else
        {
            insertElement(node->rchild, key);
        }
    }
}
二叉查詢樹刪除

刪除稍微麻煩一點，要分好幾種情況：

1、被刪除的結點沒有孩子。這種情況最簡單。直接刪除就可以了。

2、被刪除的結點只有左孩子或者只有右孩子。這種情況需要刪除當前結點，並把當前結點的孩子作為當前結點的父結點的孩子。說白了就是用當前結點的孩子替代當前結點，然後把當前結點刪除了。

3、被刪除結點同時有左孩子和右孩子。這種情況稍微複雜一點，因為二叉查詢樹的特性在替換當前結點的時候做些操作。

我們把二叉查詢樹按照中序遍歷後輸出結果中的序列中，每個元素的前一個元素稱為該元素的前驅，後面一個元素稱為該元素的後繼。如下圖：

這裡寫圖片描述

上圖是一個二叉查詢樹，按照中序遍歷的結果是3、10、20、32、33、44、45、50。則33的前驅為32，後繼為44。由二叉查詢樹的特性可知如果一個二叉搜尋樹中的一個結點有兩個孩子，那麼它的後繼沒有左孩子，它的前驅沒有右孩子。

假如想刪除結點33，則符合情況3。而情況3則是用當前結點的後繼代替當前結點，當前結點的左孩子為後繼結點的左孩子，後繼結點如果有右孩子，則把右孩子當作後繼結點父結點的左孩子。如下圖：

這裡寫圖片描述

實現程式碼如下：

template<typename T>
void replaceAByB(TreeNode<T> *A, TreeNode<T> *B)
{
    if (A == nullptr)
    {
        return;
    }
    TreeNode<T> * parent = getParent(A->data);
    if (nullptr == parent)
    {
        m_root = B;
        return;
    }
    if (parent->lchild == A)
    {
        parent->lchild = B;
    }
    else
    {
        parent->rchild = B;
    }
}

template<typename T>
TreeNode<T> * minElement(TreeNode<T> * node)
{
    if (nullptr == node->lchild)
        return node;
    else
        minElement(node->lchild);
}

template<typename T>
bool deleteElement(T key)
{
    TreeNode<T> * pCurrent = search(key);
    if (nullptr == pCurrent)
        return false;
    if (nullptr == pCurrent->lchild)// 無左孩子
    {
        replaceAByB(pCurrent, pCurrent->rchild);
    }
    else if (nullptr == pCurrent->rchild)// 無右孩子
    {
        replaceAByB(pCurrent, pCurrent->lchild);
    }
    else
    {
        TreeNode<T> * pSuccesor = minElement(pCurrent->rchild);// 找到後繼結點
        replaceAByB(pSuccesor, pSuccesor->rchild);// 後繼者是沒有左孩子的
        pSuccesor->rchild = pCurrent->rchild;
        pSuccesor->lchild = pCurrent->lchild;
        replaceAByB(pCurrent, pSuccesor);
    }
    delete pCurrent;
}

搜尋二叉樹的完整實現程式碼如下，為了方便這裡把樹封裝為一個類，二叉樹繼承自樹，二叉查詢樹繼承自二叉樹，後面要說的平衡二叉查詢樹繼承自二叉查詢樹。

#pragma once

#include <iostream>

// 樹節點
template<typename T>
class TreeNode
{
public:
    T data;
    TreeNode<T>* lchild,* rchild;

    TreeNode():lchild(nullptr), rchild(nullptr) {}
};
//------------------------------------------------------------------
// 樹
template<typename T>
class Tree
{
public:
    virtual bool insert(T key) = 0;
    virtual bool deleteElement(T key) = 0;
    virtual TreeNode<T>* search(T key) = 0;
    virtual TreeNode<T> * getParent(T key) = 0;
    virtual void deleteAll() = 0;
    Tree(): m_root(nullptr) {}
protected:
    TreeNode<T> * m_root;
};
//-----------------------------------------------------------------
// 二叉樹
template<typename T>
class BiTree : public Tree<T>
{
public:
    BiTree(){}

    virtual bool insert(T key);
    virtual bool deleteElement(T key);
    virtual TreeNode<T> * search(T key);
    virtual TreeNode<T> * getParent(T key);
    virtual void deleteAll();

    virtual void preOrderTraverse();
    virtual void inOrderTraverse();
    virtual void postOrderTraverse();
protected:
    virtual void preTraverse(TreeNode<T> * node);
    virtual void inTraverse(TreeNode<T> * node);
    virtual void postTraverse(TreeNode<T> * node);
    virtual void deleteAllElement(TreeNode<T> *& node);
};

template<typename T>
void BiTree<T>::preOrderTraverse()
{
    preTraverse(m_root);
}

template<typename T>
void BiTree<T>::inOrderTraverse()
{
    inTraverse(m_root);
}

template<typename T>
void BiTree<T>::postOrderTraverse()
{
    postTraverse(m_root);
}

template<typename T>
void BiTree<T>::preTraverse(TreeNode<T> * node)
{
    if (node)
    {
        std::cout << node->data << std::endl;
        preTraverse(node->lchild);
        preTraverse(node->rchild);
    }
}

template<typename T>
void BiTree<T>::inTraverse(TreeNode<T> * node)
{
    if (node)
    {
        inTraverse(node->lchild);
        std::cout << node->data << std::endl;
        inTraverse(node->rchild);
    }
}

template<typename T>
void BiTree<T>::postTraverse(TreeNode<T> * node)
{
    if (node)
    {
        postTraverse(node->lchild);
        postTraverse(node->rchild);
        std::cout << node->data << std::endl;
    }
}

template<typename T>
TreeNode<T> * BiTree<T>::getParent(T key)
{
    return nullptr;
}

template<typename T>
bool BiTree<T>::insert(T key)
{
    return true;
}

template<typename T>
bool BiTree<T>::deleteElement(T key)
{
    return true;
}

template<typename T>
TreeNode<T>* BiTree<T>::search(T key)
{
    return nullptr;
}

template<typename T>
void BiTree<T>::deleteAll()
{
    deleteAllElement(m_root);
}

template<typename T>
void BiTree<T>::deleteAllElement(TreeNode<T> *& node)
{
    if (nullptr == node)
        return;
    if (nullptr != node->lchild)
        deleteAllElement(node->lchild);
    else if (nullptr != node->rchild)
        deleteAllElement(node->rchild);
    node->lchild = nullptr;
    node->rchild = nullptr;
    delete node;
    node = nullptr;
}

//-------------------------------------------------------------------
// 二叉查詢樹(Binary Sort Tree)BST
template<typename T>
class TreeBST : public BiTree<T>
{
public:
    virtual bool insert(T key);
    virtual bool deleteElement(T key);
    virtual TreeNode<T>* search(T key);
    virtual TreeNode<T> * getParent(T key);

    TreeNode<T> * minElement(TreeNode<T> * node);
    TreeNode<T> * maxElement(TreeNode<T> * node);
protected:
    virtual bool insertElement(TreeNode<T> * & node, T key);
    virtual TreeNode<T> * searchElement(TreeNode<T> * node, T key);
    TreeNode<T> * getPar(TreeNode<T> * node, T key);
    virtual void replaceAByB(TreeNode<T> * A, TreeNode<T> * B);
};

template<typename T>
bool TreeBST<T>::insert(T key)
{
    return insertElement(m_root, key);
}

template<typename T>
bool TreeBST<T>::insertElement(TreeNode<T> *& node,T key)
{
    if (nullptr == node)// 空樹
    {
        node = new TreeNode<T>;
        node->data = key;
    }
    else if (key == node->data)// 已經有該關鍵字
    {
        return false;
    }
    else
    {
        if (key < node->data)
        {
            insertElement(node->lchild, key);
        }
        else
        {
            insertElement(node->rchild, key);
        }
    }
}

template<typename T>
bool TreeBST<T>::deleteElement(T key)
{
    TreeNode<T> * pCurrent = search(key);
    if (nullptr == pCurrent)
        return false;
    if (nullptr == pCurrent->lchild)// 無左孩子
    {
        replaceAByB(pCurrent, pCurrent->rchild);
    }
    else if (nullptr == pCurrent->rchild)// 無右孩子
    {
        replaceAByB(pCurrent, pCurrent->lchild);
    }
    else
    {
        TreeNode<T> * pSuccesor = minElement(pCurrent->rchild);// 找到後繼結點
        replaceAByB(pSuccesor, pSuccesor->rchild);// 後繼者是沒有左孩子的
        pSuccesor->rchild = pCurrent->rchild;
        pSuccesor->lchild = pCurrent->lchild;
        replaceAByB(pCurrent, pSuccesor);
    }
    delete pCurrent;
}

template<typename T>
TreeNode<T>* TreeBST<T>::search(T key)
{
    return searchElement(m_root, key);
}

template<typename T>
TreeNode<T> * TreeBST<T>::searchElement(TreeNode<T> * node, T key)
{
    if (nullptr == node)
        return nullptr;
    if (key == node->data)
        return node;
    else if (key < node->data)
        searchElement(node->lchild, key);
    else
        searchElement(node->rchild, key);
}

template<typename T>
TreeNode<T> * TreeBST<T>::getParent(T key)
{
    return getPar(m_root, key);
}

template<typename T>
TreeNode<T> * TreeBST<T>::getPar(TreeNode<T> * node, T key)
{
    static TreeNode<T> * parentNode = nullptr;
    if (nullptr == node)
        return nullptr;
    if (key == node->data)
    {
        // 這裡是因為返回一個值後，static指的是上一次返回結果，
        // 所以返回後需要重新賦值，用static是為了在遞迴過程中減少傳遞的引數
        TreeNode<T> * temp = parentNode;
        parentNode = nullptr;
        return temp;
    }
    else if (key < node->data)
    {
        parentNode = node;
        getPar(node->lchild, key);
    }
    else
    {
        parentNode = node;
        getPar(node->rchild, key);
    }   
}

template<typename T>
TreeNode<T> * TreeBST<T>::minElement(TreeNode<T> * node)
{
    if (nullptr == node->lchild)
        return node;
    else
        minElement(node->lchild);
}

template<typename T>
TreeNode<T> * TreeBST<T>::maxElement(TreeNode<T> * node)
{
    if (nullptr == node->rchild)
        return node;
    else
        maxElement(node->rchild);
}

template<typename T>
void TreeBST<T>::replaceAByB(TreeNode<T> *A, TreeNode<T> *B)
{
    if (A == nullptr)
    {
        return;
    }
    TreeNode<T> * parent = getParent(A->data);
    if (nullptr == parent)
    {
        m_root = B;
        return;
    }
    if (parent->lchild == A)
    {
        parent->lchild = B;
    }
    else
    {
        parent->rchild = B;
    }
}

測試程式碼如下：


#include "tree.h"
#include <iostream>

int main()
{
    int ptr[15] = { 4, 5, 7, 3, 8, 9, 1, 2, 6, 2 , 49, 23, 10, 30, 3 };
    TreeBST<int> tree;
    for (int i = 0; i < 15; i++)
    {
        tree.insert(ptr[i]);
    }
    tree.inOrderTraverse();

    std::cout << "刪除元素" << std::endl;
    tree.deleteElement(2);// 情況1
    tree.deleteElement(5);// 情況2
    tree.deleteElement(4);// 情況3
    tree.deleteElement(9);// 情況3
    tree.inOrderTraverse();
    tree.deleteAll();

    getchar();
    return 0;
}

測試結果如下圖：

這裡寫圖片描述

平衡二叉查詢樹

平衡二叉樹(Self-Balancing Binary Search Tree 或 Height-Balanced Binary Search Tree)，以一種二叉搜尋樹，其中每一個結點的左子樹和右子樹的高度差至多等於1。我們將二叉樹上結點的左子樹深度減去右子樹深度的值稱為平衡因子BF（Balance Factor）。

平衡二叉查詢樹插入

平衡二叉樹構建的基本思想就是在構建二叉搜尋樹的過程中，每當插入一個結點時，先檢查是否因插入而破壞了樹的平衡性，若是，則找出最小不平衡子樹。在爆出二叉搜尋樹特性的前提下，調整最小不平衡子樹中個結點之間的連結關係，進行相應的旋轉，使之成為新的平衡子樹。

如構建序列為：3、2、1、4、5、6、7、10、9、8的平衡二叉樹，構建過程如下：

這裡寫圖片描述

如上圖，在步驟3中，結點3的平衡因子為2大於1，所以需要做出一些調整。如步驟4，此時結點成為了根結點，結點3成為了結點2的右孩子。我們稱這種操作為以結點3為原點的右旋（順時針）。繼續插入操作，接下來是結點4。

這裡寫圖片描述

在步驟6中，結點3的平衡因子的絕對值大於1，所以要做一些調整，如步驟7，以結點3為原點，向左旋轉。這就是以結點3為原點的左旋（逆時針）。繼續：

這裡寫圖片描述

在步驟8中，結點2的平衡因子超標，需要調整，如步驟9，以結點2為原點，進行左旋。繼續：

這裡寫圖片描述

在步驟10中，結點5需要調整，如步驟11，以結點5為原點進行左旋。繼續：

這裡寫圖片描述

在步驟13中，結點7需要調整，但是結點7的右孩子（即結點10）的平衡因子與自身平衡因子符號不同。所以先以結點7的右孩子由原點進行右旋（如步驟14），然後再以當前結點，也就是結點7為原點進行左旋（如步驟15）。繼續：

這裡寫圖片描述

再步驟16中結點6，需要調整，同樣因為結點6的右孩子平衡因子與自己不同，所以先以結點6右孩子為原點進行右旋（如步驟17），然後以結點6為原點進左旋（如步驟18）。

由以上步驟我們知道，如果當前結點平衡因子大於1，並且左孩子的平衡因子符號與當前結點相同。則需要以當前結點為原點右旋。如果左孩子平衡因子符號與當前結點符號不同，則先以左孩子為原點進行左旋，然後以當前結點為原點進行右旋。同理，如果當前結點平衡因子小於-1，並且右孩子平衡因子符號與當前結點相同，則以當前結點為原點左旋。如果右孩子平衡因子符號與當前結點不同，則先以右孩子為原點進行右旋，然後以當前結點為原點進行左旋。

左旋實現：


template<typename T>
void leftRotate(TreeNode<T> * node)
{
    TreeNode<T> temp;// 臨時物件，用來中轉根節點
    TreeNode<T> * rchild = node->rchild;
    temp = * node;
    // 構建根節點
    * node = * node->rchild;
    // 構建根節點的左孩子節點
    temp.rchild = rchild->lchild;
    * rchild = temp;
    node->lchild = rchild;
}

右旋實現：


template<typename T>
void rightRotate(TreeNode<T> * node)
{
    TreeNode<T> temp;// 臨時物件，用來中轉根節點
    TreeNode<T> * lchild = node->lchild;
    temp = * node;
    // 構建根節點
    * node = * node->lchild;
    // 構建根節點的有孩子節點
    temp.lchild = lchild->rchild;
    * lchild = temp;
    node->rchild = lchild;
}

為方便操作和程式碼重用，把樹結構調整封裝入兩個函式，分別為左平衡操作和右平衡操作。如果左子樹高度大於右子樹高度超過1則左平衡操作，反之右平衡操作。這裡的平衡因子只取了三個值，分別為eh(等高)、lh(左高)、rh(右高)。實現程式碼如下：


// 平衡二叉樹結點（AVL）
template<typename T>
class TreeNodeAVL : public TreeNode<T>
{
public:
    enum {eh, lh, rh} m_bf;// 分別為等高，左高，右高
    TreeNodeAVL() : m_bf(eh) {}
};

template<typename T>
void TreeAVL<T>::leftBalance(TreeNodeAVL<T> * node)
{
    // 呼叫此函式時，node->m_bf == RH，即右邊高於左邊
    TreeNodeAVL<T> * lchildNode = (TreeNodeAVL<T> * )node->lchild, * tempNode = nullptr;
    switch (lchildNode->m_bf)
    {
    case TreeNodeAVL<T>::eh:// 平衡因子
        node->m_bf = TreeNodeAVL<T>::lh;
        lchildNode->m_bf = TreeNodeAVL<T>::rh;
        rightRotate(node);
        break;
    case TreeNodeAVL<T>::lh:// 和左孩子平衡因子相同
        node->m_bf = TreeNodeAVL<T>::eh;
        lchildNode->m_bf = TreeNodeAVL<T>::eh;
        rightRotate(node);
        break;
    case TreeNodeAVL<T>::rh:// 和左孩子的平衡因子不同，則先以左孩子為中心左旋旋，然後再右旋              
        tempNode = (TreeNodeAVL<T> * )lchildNode->rchild;// 右旋會影響到左孩子的右孩子的平衡因子
        switch (tempNode->m_bf)
        {
        case TreeNodeAVL<T>::eh:
            node->m_bf = TreeNodeAVL<T>::eh;
            lchildNode->m_bf = TreeNodeAVL<T>::eh;
            break;
        case TreeNodeAVL<T>::lh:
            node->m_bf = TreeNodeAVL<T>::eh;
            lchildNode->m_bf = TreeNodeAVL<T>::rh;
            break;
        case TreeNodeAVL<T>::rh:
            node->m_bf = TreeNodeAVL<T>::lh;
            lchildNode->m_bf = TreeNodeAVL<T>::eh;
            break;
        default:
            break;
        }
        tempNode->m_bf = TreeNodeAVL<T>::eh;
        leftRotate(lchildNode);
        rightRotate(node);
        break;
    default:
        break;
    }
}

template<typename T>
void TreeAVL<T>::rightBalance(TreeNodeAVL<T> * node)
{
    // 呼叫此函式時，node->m_bf == RH，即右邊高於左邊
    TreeNodeAVL<T> * rchildNode = (TreeNodeAVL<T> * )node->rchild, * tempNode = nullptr;
    switch (rchildNode->m_bf)
    {
    case TreeNodeAVL<T>::eh:// 平衡因子
        node->m_bf = TreeNodeAVL<T>::rh;
        rchildNode->m_bf = TreeNodeAVL<T>::lh;
        leftRotate(node);
        break;
    case TreeNodeAVL<T>::lh:// 和有孩子的平衡因子不同，則先以右孩子為中心右旋，然後在左旋
        // 右旋會影響到右孩子的左孩子的平衡因子
        tempNode = (TreeNodeAVL<T> * )rchildNode->lchild;
        switch (tempNode->m_bf)
        {
            case TreeNodeAVL<T>::eh:
                node->m_bf = TreeNodeAVL<T>::eh;
                rchildNode->m_bf = TreeNodeAVL<T>::eh;
                break;
            case TreeNodeAVL<T>::lh:
                node->m_bf = TreeNodeAVL<T>::eh;
                rchildNode->m_bf = TreeNodeAVL<T>::rh;
                break;
            case TreeNodeAVL<T>::rh:
                node->m_bf = TreeNodeAVL<T>::lh;
                rchildNode->m_bf = TreeNodeAVL<T>::eh;
                break;
            default:
                break;
        }
        tempNode->m_bf = TreeNodeAVL<T>::eh;
        rightRotate(rchildNode);
        leftRotate(node);
        break;
    case TreeNodeAVL<T>::rh:// 和右孩子的平衡因子相同，直接左旋
        node->m_bf = TreeNodeAVL<T>::eh;
        rchildNode->m_bf = TreeNodeAVL<T>::eh;
        leftRotate(node);
        break;
    default:
        break;
    }
}
刪除操作

刪除操作，並不複雜，和二叉查詢樹差不多。只是再刪除後需要考慮以下要不要調整樹結構，實現程式碼如下：


bool TreeAVL<T>::deleteElement(T key)
{
    TreeNode<T> * pCurrent = search(key);
    if (nullptr == pCurrent)
        return false;
    TreeNodeAVL<T> * pParent = (TreeNodeAVL<T> * )getParent(key);
    bool delRight;
    if (nullptr != pParent)
    {
        if (pCurrent == pParent->lchild)
        {
            delRight = false;
        }
        else
        {
            delRight = true;
        }
    }
    if (nullptr == pCurrent->lchild)// 無左孩子
    {
        replaceAByB(pCurrent, pCurrent->rchild);
    }
    else if (nullptr == pCurrent->rchild)// 無右孩子
    {
        replaceAByB(pCurrent, pCurrent->lchild);
    }
    else
    {
        TreeNode<T> * pSuccesor = minElement(pCurrent->rchild);
        replaceAByB(pSuccesor, pSuccesor->rchild);// 後繼者是沒有左孩子的
        pSuccesor->rchild = pCurrent->rchild;
        pSuccesor->lchild = pCurrent->lchild;
        replaceAByB(pCurrent, pSuccesor);
    }
    delete pCurrent;
    pCurrent = nullptr;
    // 修改相關平衡因子
    if (nullptr != pParent)
    {
        if (delRight)// 如果刪除的是右孩子
        {
            switch (pParent->m_bf)
            {
            case TreeNodeAVL<T>::lh:// 本來左高，刪除右孩子後就需要左平衡了
                leftBalance(pParent);
                break;
            case TreeNodeAVL<T>::eh:
                pParent->m_bf = TreeNodeAVL<T>::lh;
                break;
            case TreeNodeAVL<T>::rh:
                pParent->m_bf = TreeNodeAVL<T>::eh;
                break;
            default:
                break;
            }
        }
        else// 如果刪除的是左孩子
        {
            switch (pParent->m_bf)
            {
            case TreeNodeAVL<T>::lh:
                pParent->m_bf = TreeNodeAVL<T>::eh;
                break;
            case TreeNodeAVL<T>::eh:
                pParent->m_bf = TreeNodeAVL<T>::rh;
                break;
            case TreeNodeAVL<T>::rh:// 本來右高，刪除左孩子後就需要右平衡了
                rightBalance(pParent);
                break;
            default:
                break;
            }
        }
    }
}
平衡二叉樹的完整實現

這裡把平衡二叉樹封裝為一個類，繼承自前面提到的二叉搜尋樹，如下：


// 平衡二叉樹（AVL）
template<typename T>
class TreeNodeAVL : public TreeNode<T>
{
public:
    enum {eh, lh, rh} m_bf;// 分別為等高，左高，右高
    TreeNodeAVL() : m_bf(eh) {}
};

template<typename T>
class TreeAVL : public TreeBST<T>
{
public:
    TreeAVL() : m_taller(true) {}
    virtual bool insert(T key);
    virtual bool deleteElement(T key);
protected:
    virtual bool insertElement(TreeNodeAVL<T> *& node, T key);
    void leftBalance(TreeNodeAVL<T> * node);
    void rightBalance(TreeNodeAVL<T> * node);
    void leftRotate(TreeNodeAVL<T> * node);
    void rightRotate(TreeNodeAVL<T> * node);

    bool m_taller;// 元素是否增加
};

template<typename T>
bool TreeAVL<T>::insert(T key)
{
    return insertElement((TreeNodeAVL<T> *&)m_root, key);
}

template<typename T>
bool TreeAVL<T>::insertElement(TreeNodeAVL<T> *& node, T key)
{
    if (nullptr == node)// 空樹
    {
        node = new TreeNodeAVL<T>;
        node->data = key;
        node->m_bf = TreeNodeAVL<T>::eh;
        m_taller = true; // 元素增加
    }
    else if (key == node->data)// 已經有該關鍵字
    {
        m_taller = false; // 元素未增加
        return false;
    }
    else
    {
        if (key < node->data)
        {
            if (!insertElement((TreeNodeAVL<T> *&)node->lchild, key))
                return false;
            if (m_taller)// 元素增加要修正平衡因子
            {
                switch (node->m_bf)
                {
                case TreeNodeAVL<T>::eh:
                    node->m_bf = TreeNodeAVL<T>::lh;
                    m_taller = true;  // 上層也要響應的修改平衡因子
                    break;
                case TreeNodeAVL<T>::lh:
                    leftBalance(node);// 說明現在已經是左邊過高了，所以要平衡
                    m_taller = false; // 已經經過平衡，則不用再平衡
                    break;
                case TreeNodeAVL<T>::rh:
                    node->m_bf = TreeNodeAVL<T>::eh; // 因為原來右高，現在左邊新增一元素，則平衡
                    m_taller = false;
                    break;
                default:
                    break;
                }
            }
        }
        else
        {
            if (!insertElement((TreeNodeAVL<T> *&)node->rchild, key))
                return false;
            if (m_taller)// 元素增加要修正平衡因子
            {
                switch (node->m_bf)
                {
                case TreeNodeAVL<T>::eh:
                    node->m_bf = TreeNodeAVL<T>::rh;
                    m_taller = 
            
  

           

              
              

            

            
相關推薦

			   
            
            
            
 

    


    
    
資料結構（排序演算法和查詢演算法的時間複雜度和空間複雜度）

     
  
 
 這是從大神給多的網站上找到的演算法的時間複雜度趨勢和各個常用結構的複雜度截圖。 
  
   
  
   
 演算法的時間複雜度，用來度量演算法的執行時間，記作: T(n) = O(f(n))。它表示隨著 輸入大小n 的增大，演算法執行需要的時間的增長速度可以用 f(n) 來描 



  
 

    


    
    
資料結構（樹，二叉搜尋樹，平衡二叉樹 C++實現）

     
 
							
							
							樹

樹（Tree）是n（n>=0）個結點的有限集合。n = 0時稱為空樹。在任意一顆非空樹中：(1)有且僅有一個特定的稱為根（Root）的結點；（2）當n > 1時，其餘結點可分為m （m > 0）個互不相交的有限集 T1T1 、 T2T2  



  
 

    


    
    
資料結構（C語言實現）：判斷兩棵二叉樹是否相等，bug求解

     
 
                判斷兩棵二叉樹是否相等。

遇到了bug，求大神幫忙！！！

C語言原始碼：

#include <stdio.h>
#include <stdlib.h>
#include <malloc.h>
#define OK 1
#define  



  
 

    


    
    
資料結構（三）:非線性邏輯結構-特殊的二叉樹結構：堆、哈夫曼樹、二叉搜尋樹、平衡二叉搜尋樹、紅黑樹、線索二叉樹

     
 /* 
性質1. 節點是紅色或黑色 
性質2. 根是黑色 
性質3. 每個紅色節點的兩個子節點都是黑色 (從每個葉子到根的所有路徑上不能有兩個連續的紅色節點) 
性質4. 從任一節點到其每個葉子的所有路徑都包含相同數目的黑色節點 
*/ 

#include  
#include  
typedef enum 



  
 

    


    
    
資料結構（棧，佇列，連結串列，二叉樹）

     
 
							
							
							棧

棧作為一種資料結構，用途十分廣泛。在回撥函式等許多場景中都有應用。我們需要了解它的基本用途，那就是先進後出和佇列的先進先出正好相反。

最近在學習資料結構和演算法，於是自己來實現。我特別喜歡C語言的指標，我發現很好用，於是用C++來實現一個簡單的範例。 
 



  
 

    


    
    
再談資料結構（二）數和二叉樹

     
  
  
  
 1 - 引言 
 關於樹和二叉樹，我們需要達到的能力有： 
  
  熟悉樹和二叉樹的有關概念 
  熟悉二叉樹的性質 
  熟練掌握遍歷二叉樹的遞迴演算法，並靈活運用 
  遞迴遍歷二叉樹及其應用 
  
 本文著重在樹和二叉樹實際應用與程式碼實現基本操作，對概念就不再贅述 
 2 - 二 



  
 

    


    
    
資料結構（四）之二叉樹

     
  
  
  
  
   二叉樹  
  
 二叉樹可以用陣列和鏈式結構這兩種方式來建立，這裡只介紹二叉樹的鏈式結構，並且實現二叉樹的前序、中序和後序遍歷。（運用二叉樹組定義靜態二叉樹的方式以註釋的形式寫明） 二叉樹的建立有三種方式：前序、中序和後序。這裡只展現了前序遍歷的方式。 
 #include< 



  
 

    


    
    
資料結構（四）二叉樹的遍歷

     
 
							
							
							
二叉樹的遍歷
0. 樹的表示
typedef struct TreeNode *BinTree;
struct TreeNode{
	int Data;  // 存值 
	BinTree Left;    // 左兒子結點 
	BinTree Right;   



  
 

    


    
    
資料結構之二叉搜尋樹的簡單實現(C++實現）

     
  
  
  
 功能 
 插入：insert() 查詢：search() 刪除：remove() 清除整個樹：clear() 最大值：max() 最小值：min() 前序遍歷：PreOrder() 中序遍歷：InOrder() 後序遍歷：PostOrder() 注：此二叉樹允許插入相同的值，且預設將其放在右 



  
 

    


    
    
資料結構（C++） 二叉樹模板類

     
 
							
							
							1.二叉樹


  遞迴定義：一顆二叉樹是結點的有限的集合，該集合或者為空或者是由一個根節點加上兩顆分別稱為左子樹和右子樹、互不相交的二叉樹的組合。 
  二叉樹的左右子樹都還是二叉樹，到達空子樹的時候遞迴定義結束。許多基於二叉樹的演算法都利用了這個遞迴特性。  



  
 

    


    
    
資料結構（一）-----二叉樹

     
  
 
   
 一、二叉樹簡介 
 1、二叉樹簡介 
 二叉樹是由n（n>=0）個結點組成的有序集合，集合或者為空，或者是由一個根節點加上兩棵分別稱為左子樹和右子樹的、互不相交的二叉樹組成。 
   
   
  
 性質一：對於任何一棵二叉樹T，若葉子節點數為n0，度數 



  
 

    


    
    
資料結構（四）之非遞迴遍歷二叉樹

     
  
  
  
 void Inoder(Bitree root)//二叉樹的中序遍歷非遞迴 
{
	IniStack(&S);//初始化一個棧
	p=root;
	while(!isEmpty(S)||p!=NULL)
	{
		if(p!=NULL)//如果當前結點不為空進棧 
		{
			pu 



  
 

    


    
    
資料結構（七）——樹結構(Tree) 之二叉樹的常用操作

     
  
 
 一.鏈式儲存的二叉樹的操作 
 1.遍歷二叉樹 
 
  先序遍歷：根-->左-->右 
  中序遍歷：左-->根-->右 
  後序遍歷：左-->右-->根 
 
 2.二叉樹結點的查詢  
 結點的查詢也可以分為先序查詢，中序查詢和後序查詢。方式和遍 



  
 

    


    
    
淺談演算法和資料結構（7）：二叉查詢樹

     
 

        			
		
		前文介紹了符號表的兩種實現，無序連結串列和有序陣列，無序連結串列在插入的時候具有較高的靈活性，而有序陣列在查詢時具有較高的效率，本文介紹的二叉查詢樹(Binary Search Tree，BST)這一資料結構綜合了以上兩種資料結構的優點。
二叉查詢樹具有很高的靈活性 



  
 

    


    
    
資料結構（六）——二叉樹 前序、中序、後序、層次遍歷及非遞迴實現 查詢、統計個數、比較、求深度的遞迴實現

     
 
								
								            
						
                一、基本概念每個結點最多有兩棵子樹，左子樹和右子樹，次序不可以顛倒。性質：1、非空二叉樹的第n層上至多有2^(n-1)個元素。2、深度為h的二叉樹至多有2^h-1個結點。滿二叉樹：所有終端都在同一層次， 



  
 

    


    
    
資料結構（七）二叉樹節點、空指標、刪除葉節點、最大節點數

     
 
                1、二叉樹節點

程式碼:

//二叉樹節點 
#include<stdio.h>
#include <malloc.h>
#include <conio.h>
#include<iostream>
//
typedef int 



  
 

    


    
    
資料結構（樹和二叉樹的轉換與遍歷）

     
 
								
								            
							
							
							二叉樹的遍歷

 
先序遍歷(DLR)：先遍歷根節點，再遍歷左子樹，最後遍歷右子樹 
遍歷結果：ABDHIEJCFG

 public void PreOrder(Node<T> root) 



  
 

    


    
    
一本正經的聊資料結構（6）：最優二叉樹 —— 哈夫曼樹

     
 ![](https://cdn.geekdigging.com/DataStructure/head.png)

前文傳送門：

[「一本正經的聊資料結構（1）：時間複雜度」](https://www.geekdigging.com/2020/03/28/6072951828/)

[「一本正經的聊資料結構（ 



  
 

    


    
    
Java資料結構（十四）—— 平衡二叉樹（AVL樹）

     
 平衡二叉樹（AVL樹）
二叉排序樹問題分析


左子樹全部為空，從形式上看更像一個單鏈表


插入速度沒有影響


查詢速度明顯降低


解決方案：平衡二叉樹


基本介紹


平衡二叉樹也叫二叉搜尋樹，保證查詢效率較高


它是一棵空樹或它的左右兩個子樹的高度差的絕對值不超過1，並且左右兩棵子樹都是一棵平衡 



  
 

    


    
    
從零開始_學_資料結構（二）——樹的基本概念

     
 
                
相比之前的帖子，對其進行了增添和完善。

ps：本顏色的字型是後續新增內容
——————————————————

參考連結：
大話資料結構.pdf

http://www.cnblogs.com/yc_sunniwell/archive/2010/06/27/176623